Achilles paradox, in logic, an argument attributed to the 5th-century-bce Greek philosopher Zeno, and one of his four paradoxes described by Aristotle in the treatise Physics. The paradox concerns a race between the fleet-footed Achilles and a slow-moving tortoise.The two start moving at the same moment, but if the tortoise is initially given a head start and continues to move ahead, Achilles. History. The origins of the paradoxes are somewhat unclear, but they are generally thought to have been developed to support Parmenides' doctrine of monism, that all of reality is one, and that all change is impossible [clarification needed]. Diogenes Laërtius, citing Favorinus, says that Zeno's teacher Parmenides was the first to introduce the paradox of Achilles and the tortoise.

Ninotchka Illustrations Achilles and the Tortoise www.ninotchka.nl Tortoise, Myths, Zelda
Achilles laughed louder than ever. "You will surely lose, my friend, in that case," he told the Tortoise, "but let us race, if you wish it.". "On the contrary," said the Tortoise, "I will win, and I can prove it to you by a simple argument.". "Go on then," Achilles replied, with less confidence than he felt before. "What the Tortoise Said to Achilles", written by Lewis Carroll in 1895 for the philosophical journal Mind, is a brief allegorical dialogue on the foundations of logic.The title alludes to one of Zeno's paradoxes of motion, in which Achilles could never overtake the tortoise in a race. In Carroll's dialogue, the tortoise challenges Achilles to use the force of logic to make him accept the. Zeno's Paradoxes. First published Tue Apr 30, 2002; substantive revision Mon Jun 11, 2018. Almost everything that we know about Zeno of Elea is to be found in the opening pages of Plato's Parmenides. There we learn that Zeno was nearly 40 years old when Socrates was a young man, say 20. Since Socrates was born in 469 BC we can estimate a. In the first of a series on paradoxes, we take a look at Zeno's famous paradox of motion. Zeno argues that the Greek hero Achilles could never catch a tortoi.

Achilles and a turtle about infinite sequences Learning Driven
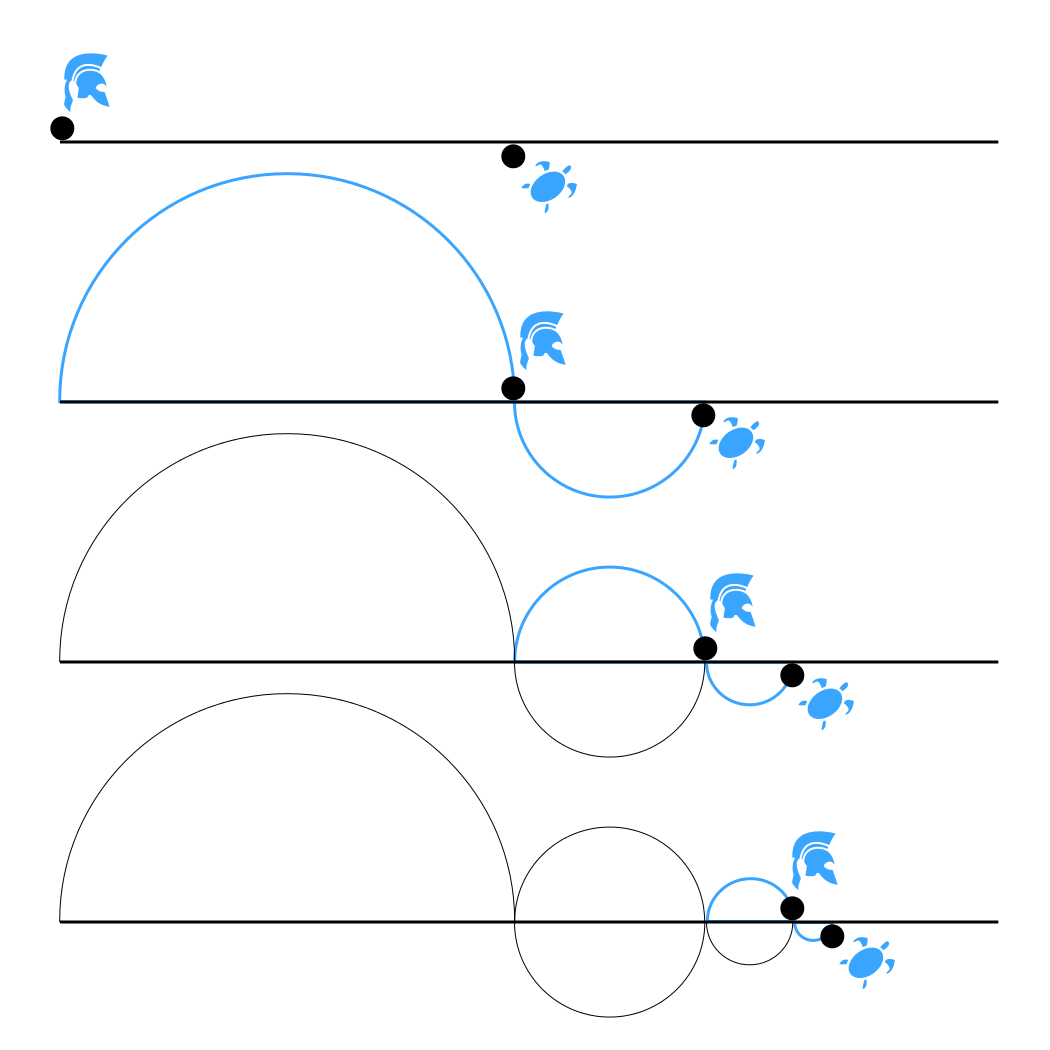
If Achilles runs the first part of the race at 1/2 mph, and the tortoise at 1/3 mph, then they slow to 1/3 mph and 1/4 mph, and so on, the tortoise will always remain ahead. But don't tell your. Achilles travels a distance d 1 in reaching the point x 1 where the tortoise starts, but by the time Achilles reaches x 1, the tortoise has moved on to a new point x 2. When Achilles reaches x 2, having gone an additional distance d 2, the tortoise has moved on to point x 3, requiring Achilles to cover an additional distance d 3, and so forth. Achilles the warrior is in a footrace with a tortoise, but Achilles has given the tortoise a 100-meter head start. If Achilles runs 10 times as fast as the tortoise, by the time he catches up to. See an explanation on Zeno's Achilles paradox, an infinite series concept used in finance to pay off mortgages. Know about the grandfather paradox and the concept of traveling back in time. Examine what is known about the ancient Athenian philosopher Socrates from Plato's dialogues and other sources. Learn about the six famous paradoxes in.

Achilles and the Tortoise Mark Tansey The Broad
Analogically to (1), one can juxtapose the paradox of the Liar (for Lewis Carroll's paradox) and that of the arrow (for "Achilles and the Turtle"), i.e. a logical paradox, on the one hand, and an aporia of motion, on the other hand, suggesting a shared formal structure Achilles's and the turtle is no paradox at all, but a refutation of the hypotheses that the space is continuous. Zeno's arrow paradox is a refutation of the hypothesis that the space is discrete. Together they form a paradox and an explanation is probably not easy. For Zeno the explanation was that what we perceive as motion is an illusion.
Zeno looks at this differently. In the time it takes Achilles to run the 0.9m to where the tortoise started, the tortoise will have travelled 0.09m. Achilles now runs this 0.09m, but the tortoise has travelled a further 0.009m. Achilles runs this only to find the tortoise has moved another 0.0009m ahead and so on for infinity. As explained in IEP's entry regarding Zeno's Paradox, current solution (aka Standard Solution) is based on the mathematics of the infinite, developed after 17th Century.. Current mathematical solution makes sense of an infinite sum having a finite amount.. This is not so for ancient mathematics and philosophy, as well as for Aristotle: either the quantities that we have to add are zero, in.
Achilles and a turtle about infinite sequences Learning Driven
Achilles and the turtle stand at the starting line of the race for any finite distance. Achilles can run 2 times faster than the turtle, and therefore allows the turtle to move a certain distance from the start (we will call it d and assume it is smaller than 1/2 of the total distance). Achilles is running 2 times faster than the turtle, so. Ancient mathematical trickery proves that a mighty hero cannot overtake a tortoise (And that mortgages take a long time to pay off).(Part 1 of 6)Playlist lin.




