Multi-species Nrn1 Protein, High Purity & Specific Bioactivity! #1 jav 35 0 I know lim n^ (1/n) = 1 n->infininity Does anyone have ideas on how to prove this? I feel like its something simple I am missing. Thanks Last edited: Mar 19, 2010 Physics news on Phys.org Using 'Kerr solitons' to boost the power of transmission electron microscopes First direct imaging of tiny noble gas clusters at room temperature

lim(n!/(mn)^n)^1/n is equal to ? n>infinity askIITians
Answer link Answer: 1/n Factorial mean multiply the all the number by counting down. ( (n-1)!)/ (n!) = [ (n-1) (n-2) (n-3)!]/ ( (n) (n-1) (n-2) (n-3)! = [cancel ( (n-1) (n-2) (n-3)!)]/ ( (n)cancel ( (n-1) (n-2) (n-3)!) = 1/n 28 Find limn→∞((n!)1/n) lim n → ∞ ( ( n!) 1 / n). The question seemed rather simple at first, and then I realized I was not sure how to properly deal with this at all. My attempt: take the logarithm, limn→∞ ln((n!)1/n) = limn→∞(1/n) ln(n!) = limn→∞(ln(n!)/n) lim n → ∞ ln ( ( n!) 1 / n) = lim n → ∞ ( 1 / n) ln ( n!) = lim n → ∞ ( ln ( n!) / n) Algebra Simplify (n-1) (n+1) (n − 1) (n + 1) ( n - 1) ( n + 1) Expand (n−1)(n+ 1) ( n - 1) ( n + 1) using the FOIL Method. Tap for more steps. n⋅n+n⋅ 1−1n−1⋅1 n ⋅ n + n ⋅ 1 - 1 n - 1 ⋅ 1 Simplify terms. Tap for more steps. n2 − 1 n 2 - 1 The quotient N − 1 N − 1 instead of N N just makes computations nicer and obviates the need to haul around factors like 1 − 1/N 1 − 1 / N. The full answer to this question would have to introduce the sampling inference where the sample indicators are random, and the values of observed characteristics y y are FIXED. Non-random. Set in stone.

[B!] 新型「NONE」乗って確かめた進化の本気度 試乗記 東洋経済オンライン 経済ニュースの新基準
This video explains how to answer questions on Ratio - Expressing as 1:n. Home GCSE MATHS Number Number Sequences In the sequence 2, 4, 6, 8, 10. there is an obvious pattern. Such sequences can be expressed in terms of the nth term of the sequence. In this case, the nth term = 2n. To find the 1st term, put n = 1 into the formula, to find the 4th term, replace the n's by 4's: 4th term = 2 × 4 = 8. Number Sequences n! = n × (n−1)! Which says "the factorial of any number is that number times the factorial of (that number minus 1) " So 10! = 10 × 9!,. and 125! = 125 × 124!, etc. What About "0!" Zero Factorial is interesting. it is generally agreed that 0! = 1. 1. Expected values of probability distributions. 2. Expected values of sums of independent random variables. If you are comfortable with these three things, the proof is easily accessible. If you are not comfortable with these things, the proof may seem like picking things out of thin air.
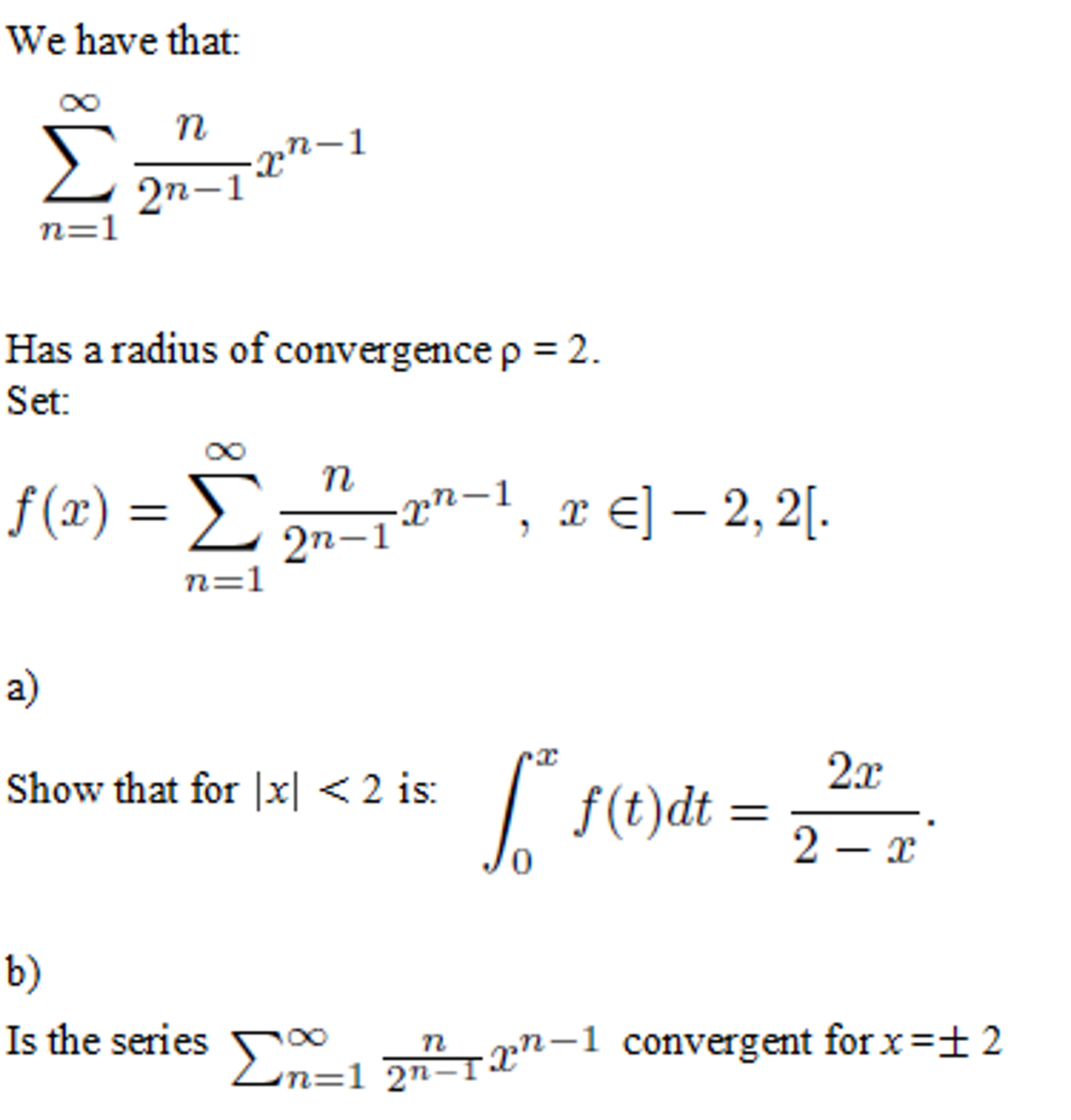
Solved We have that sigman = 1^infinity n/2^n 1 x^n 1
Knowing n-1 scores and the sample mean uniquely determines the last score so it is NOT free to vary. This is why we only have "n-1" things that can vary. So the average variation is (total variation)/(n-1). total variation is just the sum of each points variation from the mean.The measure of variation we are using is the square of the distance. The n-1 equation is used in the common situation where you are analyzing a sample of data and wish to make more general conclusions. The SD computed this way (with n-1 in the denominator) is your best guess for the value of the SD in the overall population.
The Triangular Number Sequence is generated from a pattern of dots which form a triangle: By adding another row of dots and counting all the dots we can find the next number of the sequence. But it is easier to use this Rule: x n = n (n+1)/2. Example: the 5th Triangular Number is x 5 = 5 (5+1)/2 = 15, The exponent says how many times to use the number in a multiplication. A negative exponent means divide, because the opposite of multiplying is dividing. A fractional exponent like 1/n means to take the nth root: x (1 n) = n√x. If you understand those, then you understand exponents!

probability How do you get (n1)! \over n! from 1 \over n Mathematics Stack Exchange
Rather (n+1)!= (n+1)(n)(n−1)! now just cancel it with (n−1)! thats all. Solve for k ∈ Z such that f (19992π) = 2k1 where f (x) = ∏n=1999 cos(nx). You are on the right track. But you need to do this not mod p but modulo pα, where α is the largest power of p dividing n. series 1/ ( (1 + 1/n)^n) Have a question about using Wolfram|Alpha? Give us your feedback ». Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music….