Mapas Mentais sobre FUNÇÃO QUADRATICA Última atualização em 09/08/2023 1 2. 4 Todos os mapas mentais da página 1 FUNÇÃO QUADRÁTICA: CONCEITOS FUNDAMENTAIS #função quadrática #interceptação #eixo das ordenadas #concavidade #ponto mínimo #ponto máximo #fórmula de bhaskara COMPARTILHAR DOWNLOAD FUNÇÃO QUADRÁTICA: FÓRMULAS E ANÁLISE Função quadrática ou função do segundo grau é uma aplicação F de → que associa a cada x o elemento (ax² + bx + c) ∈ , em que a, b e c são números reais dados e a ≠ 0. Pois se a = 0, não teremos mais uma função quadrática e sim uma função afim: y = bx +c. Relembrando: O que é função?

MAPA MENTAL SOBRE FUNÇÃO QUADRÁTICA STUDY MAPS
Função Quadrática Navegue pelo fascinante universo de 'Função de 2 Grau' com os nossos abrangentes mapas mentais. fevereiro 11, 2023 0 ANÁLISE COMBINATÓRIA fevereiro 14, 2023 Deixe uma resposta O mapa mental exposto trata-se do tema de: FUNÇÃO QUADRÁTICA, de maneira otimizada. O site é novo, por isso ainda não possui acervo grande de mapas mentais. Nesta aula vou te ensinar a resolver questões sobre função do 2º grau ou quadrática (Equação, raízes, construção de gráficos, vértice da parábola ( valor máx. AJUDE o canal a crescer, INSCREVA-SE, DEIXA O LIKE E COMPARTILHE! https://www.youtube.com/c/Matem%C3%A1ticaPorreta/videosFunção do segundo grau, quadrática.
Função quadrática(Mapa Mental) Matemática
Função Quadrática - Mapas Mentais de Matemática Para o Enem e Vestibulares | Projeto Elisa - Mind Maps Se usarmos a fórmula quadrática x = − b ± √b2 − 4ac 2a ,, ax2 + bx + c = 0 para resolver os interceptos x, ou zeros, descobrimos que o valor da x metade entre eles é sempre x = − b 2a, a equação para o eixo de simetria. 5.2.4 A figura representa o gráfico da função quadrática escrito em forma geral como y = x2 + 4x + 3. Dê uma olhada em nosso Mapa Mental interativo sobreFunção Quadrática, ou crie seu próprio Mapa Mental usando nosso criador de mapas mentais baseado em nuvem. Take a look at our interactive learning Mind Map about FUNÇÃO QUADRÁTICA, or create your own Mind Map using our free cloud based Mind Map maker.

MAPA MENTAL SOBRE FUNÇÃO QUADRÁTICA STUDY MAPS
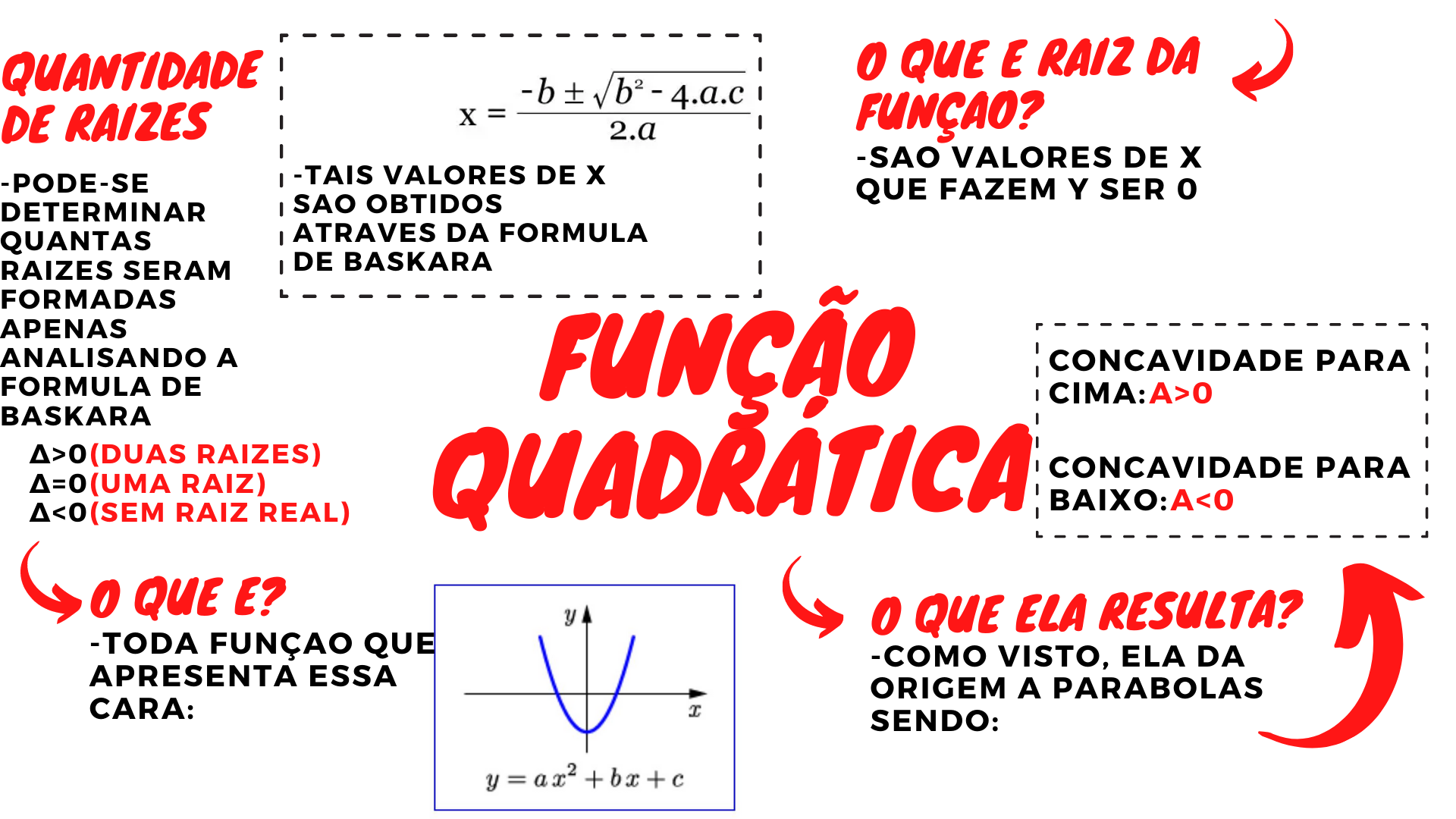
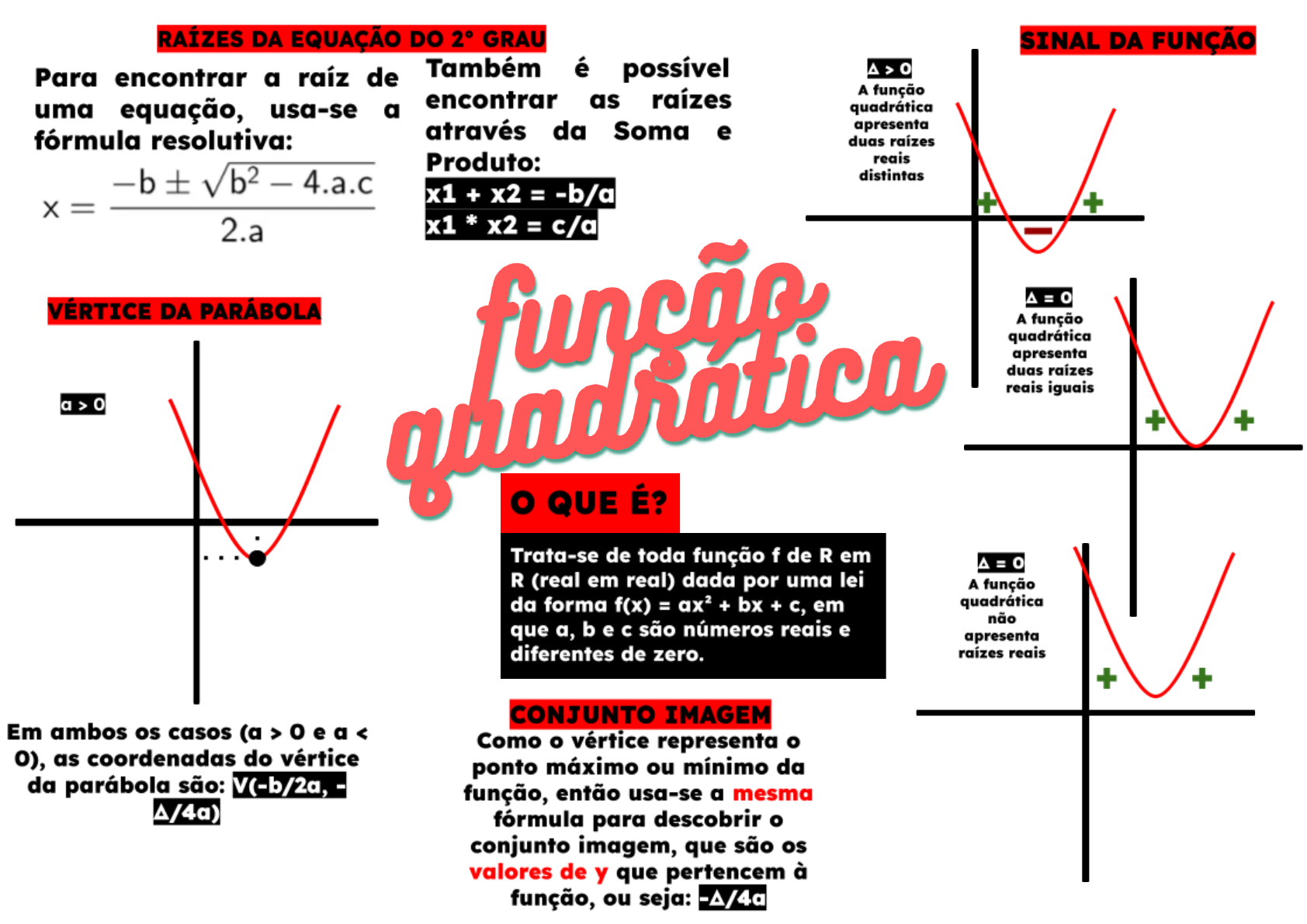
A função quadrática é uma função real que pode ser escrita da seguinte forma: f (x) igual a "ax² mais bx mais c", com "a", "b" e "c" sendo números reais e "a" sendo diferente de zero. Em nossa função que usamos como exemplo, "a" é igual a -1, mesmo ele não aparecendo explicitamente. "b" é igual a 600 e "c" é igual. CANNICA MAPA MENTAL FUNO QUADRTICA Ponto Mximo: a > 0 Im [ yV; + ) f (x) = a (x xV) + yV Ponto Mnimo: a < 0 Im (-; Yv ) CONCAVIDADE GERAL a > 0: a < 0: f (x) = ax2 + bx + c VRTICE DA PARBOLA V (xV; yV) FATORADA FORMAS f (x) = a (x x1). (x-x2) para a 0 xV = Yv = - b /2a ou - /4a FUNO QUADRTICA (x1+x2)/2 X = - b +/- Funo Polinomial do 2o Grau 2a
1 0 Resource summary Funções quadráticas Uma função definida por um polinômio do 2º grau se chama função quadrática Exemplos de funções quadráticas em x: f (x) = - 2 x² + x + 1 g (x) = 4 x² - 5 h (x) = x² Uma função quadrática é uma função da forma f (x) = a x² + b x + c onde a, b e c são números reais a ≠ 0. 1 0 Resource summary Função Quadratica Forma geral é ax²+b²+c assim podemos calcular os zeros da função que são complexos, distintos e iguais calculados através da formula de baskára depende do valor delta=b²-4.a.c dominio D=R representada através de um grafíco depende do coeficiente "a" parabola pra cima ou pra baixo possui o ponto do vertice
Mapa Mental Sobre Função Quadrática ENSINO
A função quadrática, também chamada de função polinomial de 2º grau, é uma função representada pela seguinte expressão:. f(x) = ax 2 + bx + c. Onde a, b e c são números reais e a ≠ 0.. Exemplo:. f(x) = 2x 2 + 3x + 5,. sendo, a = 2 b = 3 c = 5. Nesse caso, o polinômio da função quadrática é de grau 2, pois é o maior expoente da variável. FUNÇÃO QUADRÁTICA 1. PARÁBOLA 1.1. o gráfico será definido pelos fatores: 1.2. CONCAVIDADE 1.2.1. definido pelo parâmetro a: 1.2.2. a > 0, a concavidade da parábola será para CIMA 1.2.3. a < 0, a concavidade da parábola será para BAIXO 1.3. VÉRTICE 1.3.1. para a > 0 1.3.1.1. CRESCENTE 1.3.1.1.1. X > Xv 1.3.1.2. DECRESCENTE 1.3.1.2.1. X < Xv




