Mapas Mentais sobre PLANO CARTESIANO - Study Maps Mapas Mentais sobre PLANO CARTESIANO Última atualização em 09/08/2023 1 2. 4 Todos os mapas mentais da página 1 NÚMEROS COMPLEXOS NO PLANO CARTESIANO #matemática #números complexos #unidade imaginária #módulo #parte real #parte imaginária #distância COMPARTILHAR DOWNLOAD O mapa mental exposto trata-se do conteúdo de: PLANO CARTESIANO, de maneira otimizada. Lembrando, todos os mapas mentais aqui postados estarão sempre e disposição de todos os nossos visitantes. Porém, não se esqueça: Compartilhe o nosso site com um amigo ou até mesmo um professor, para que assim, todos sejamos felizes. =)
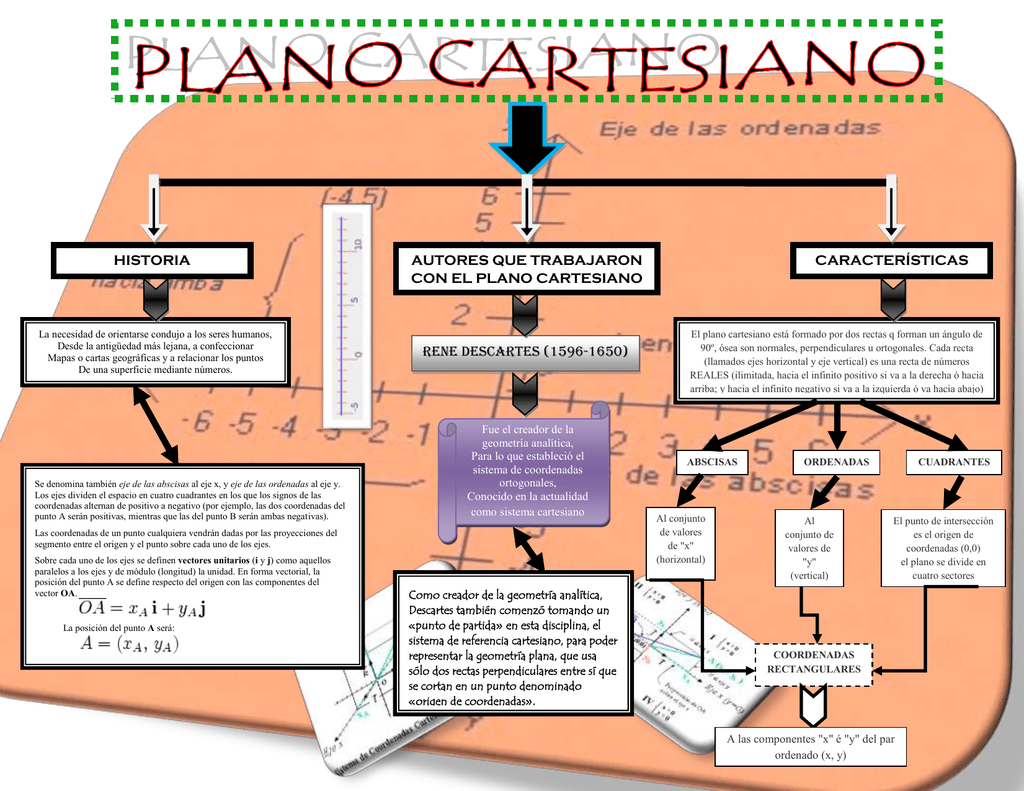
MAPA CONCEPTUAL DEL PLANO CARTESIANO
Aprenda sobre Plano Cartesiano de forma rápida e simples, através de um mapa mental que vai direto ao assunto! Plano cartesiano é um método criado pelo filósofo e matemático francês, René Descartes. Trata-se de dois eixos perpendiculares que pertencem a um plano em comum. Descartes criou esse sistema de coordenadas para demostrar a localização de alguns pontos no espaço. Plano Cartesiano. Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a dos rectas numéricas perpendiculares, una horizontal y otra vertical, que se cortan en un punto llamado origen o punto cero. La finalidad del plano cartesiano es describir la posición o ubicación de un punto en el plano, la cual está. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

MAPA MENTAL SOBRE PLANO CARTESIANO STUDY MAPS
Echa un vistazo a nuestro Mapa Mental interactivo sobre Plano Cartesiano o crea el tuyo propio usando nuestras herramientas de creación alojadas en la nube. Echa un vistazo a nuestro Mapa Mental interactivo sobre PLANO CARTESIANO o crea el tuyo propio usando nuestras herramientas de creación alojadas en la nube. Iniciar Sesión. PLANO CARTESIANO Descripción. matemáticas Mapa Mental sobre PLANO CARTESIANO, creado por Alba Cimare Martínez Fuentes el 04/05/2020. plano cartesiano. Mind Map on PLANO CARTESIANO, created by csantandercl on 13/10/2013. Mind Map by csantandercl, updated more than 1 year ago More Less Created by csantandercl about 10 years ago 28 0 0 Resource summary. PLANO CARTESIANO ¿QUE ÉS? SISTEMA DE REFERENCIA ¿EN QUÉ CONSISTE? equipo 1 Mapa mental plano cartesiano Ubicación de puntos y distancia entre ellos Localización de lugares geométricos TRABAJO DEL EQUIPO DURANTE LA realización DE LA MAQUETA ¿Qué es un plano cartesiano

Plano Cartesiano Mapa Mental LEARNBRAZ
Características del plano cartesiano. - Tanto el eje x como el eje y se extienden infinitamente por ambos extremos, y se intersectan entre sí perpendicularmente (en un ángulo de 90 grados). Esta característica se llama ortogonalidad. - El punto donde ambos ejes se intersectan se conoce como origen o punto cero. Já funções de primeiro grau são representadas por retas no plano cartesiano. Na vida prática, o plano cartesiano também é muito útil. Por sua capacidade de fornecer uma representação do espaço, o sistema cartesiano é fundamental, por exemplo, na arquitetura e na construção civil, já que é usado como base para a elaboração da.
El Plano Cartesiano El Plano Cartesiano es un diagrama que permite localizar puntos específicamente dentro de un sistema de coordenadas que se conocen como Coordenadas Rectangulares, ya que para localizar cada punto P (x,y), debes avanzar la distancia indicada por la coordenada x sobre el eje horizontal y la distancia y sobre el eje vertical. Haz click encima de cada punto y cambia su. Olá pessoal.Nesta vídeo-aula vamos falar sobre a simetria de reflexão do ponto no plano cartesiano.

MAPA MENTAL SOBRE PLANO CARTESIANO Maps4Study
1 2 Posts Relacionados Conheça 'Função Afim' em profundidade com nossos mapas mentais, projetados para simplificar conceitos complexos. m<0 y=-mx+n m>0 y=mx+n "m" es indeterminado la recta es paralela al eje "Y" x=a COMPARACIÓN DE PENDIENTE ParalelasYPerpendiculares PENDIENTES IGUALES SON PARALELAS Condición para 2 rectas sean perpendiculares EL PRODUCTO DE SUS PENDIENTES ES IGUAL A -1 SON PERPENDICULARES Me Gusta este mapa 17.2k visitas




