Exercício sobre circunferência posições relativas de duas circunferências. 01) Na figura abaixo, os segmentos AB e CD e as retas r e s recebem, respectivamente, os seguintes nomes: a) raio, corda, tangente e secante. b) raio, diâmetro, secante e tangente. c) corda, diâmetro, tangente e secante. d) corda, diâmetro, secante e tangente. Apresentaremos agora duas formas práticas para determinarmos a posição relativa entre uma reta e uma circunferência. Para tanto, examinaremos as relações entre a reta r: 2x + y - 1 = 0 e a circunferência λ: (x + 3)² + (y - 4)² = 25. 2x + y - 1 = 0 é a equação geral da reta r, onde a=2, b=1 e c=-1.

21 POSIÇÕES RELATIVAS ENTRE RETA E CIRCUNFERÊNCIA YouTube
Teste os seus conhecimentos: Faça exercícios sobre Circunferência: Posições Relativas e veja a resolução comentada. Publicado por: Marcos Noé Pedro da Silva. Imprimir. Questão 1. O centro de uma circunferência é o ponto médio do segmento AB, sendo A (4; -7) e B (-8; -3). Introdução. Dada uma reta r r de equação geral: ax+by+c= 0 a x + b y + c = 0. E uma circunferência λ λ de raio R R com centro no ponto: C(xC,yC) C ( x C, y C) Então, há três possíveis posições relativas entre a reta e a circunferência. A análise é feita a partir da distância dr,C d r, C entre o centro C C a reta r r em. Questão 10 sobre Posições Relativas entre Ponto, Reta e Circunferência: (UECE 2015) No referencial cartesiano ortogonal usual, a medida da área do quadrilátero convexo cujos vértices são as interseções de cada uma das retas x + y - 1 = 0 e x + y + 1 = 0 com a circunferência x 2 + y 2 = 25, calculada com base na unidade de comprimento (u.c.) adotada no referencial cartesiano. As relações de posição entre elementos no plano constituem a base de diversos estudos para a geometria analítica. As posições relativas entre circunferência e reta e posições relativas.

POSIÇÕES RELATIVAS ENTRE RETA E CIRCUNFERÊNCIA YouTube
Verifique a posição relativa entre as retas s: x - 2y -1 = 0, t:. Equação reduzida da circunferência: Exemplos e Exercícios. 4. Equação geral da circunferência. 5.. Posições relativas entre reta e circunferência. 9. Posições relativas entre reta e circunferência: Exemplos e Exercícios Posições relativas, através de distâncias entre o centro e a reta. Podemos dizer qual a posição de uma reta em relação a circunferência, analisando a distância do centro até a reta. Considere uma reta t e uma circunferência de centro O e raio r. Seja d = a distância entre o centro da circunferência e a reta t. Teremos três. Unidade 6: Equação da reta e posição relativa entre retas e circunferência. 600 pontos de domínio possíveis. Dominado. Proficiente. Familiar. Tentativa. Não iniciado. Questionário. Teste da unidade. Posições relativas entre uma reta e uma circunferência. Qual é o valor de w , sabendo que a reta de equação x − y + w = 0 é tangente à circunferência de equação x 2 + y 2 = 9 ? Enroscou? Usar uma dica. Aprenda Matemática, Artes, Programação de Computadores, Economia, Física, Química, Biologia, Medicina, Finanças, História e.
PosiçãO Relativa Entre Reta E CircunferêNcia
Posição relativa entre ponto e circunferência. Utilizando-se o mesmo raciocínio do item anterior determina-se a distância entre o ponto P (xp, yp e o centro da circunferência por intermédio da fórmula: a) Se d > R, o ponto é externo à circunferência. b) Se d = R, o ponto pertence à circunferência. c) Se d < R, o ponto é interno à. A fórmula geral de uma equação da circunferência é dada por (x - a)² + (y - b)² = r², dessa forma: Coordenadas do centro: (-3; 4) Medida do raio: 5. Determinando a distância entre o centro e a reta Reta r: 2x + y - 1 = 0. Temos que a distância é menor que o raio, pois 1,3 < 5. Dessa forma, a reta é secante à circunferência.
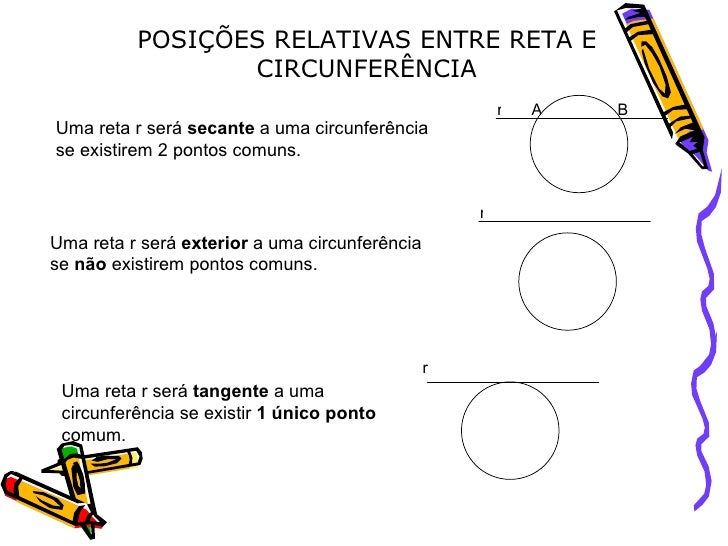
A posição relativa entre uma reta e uma circunferência está relacionada ao número de pontos que essas duas figuras podem compartilhar entre si. Reta tangente, externa ou secante são as posições entre reta e circunferência. Quando uma reta e uma circunferência são definidas sobre um mesmo plano, podemos analisar as posições que cada. Reta Posição relativa à circunferência t Tangente s Secante u Externa Correção. Foco no conteúdo Reta secante. verifique, na prática, as três posições relativas entre reta e circunferência, que são externa, tangente e secante, fazendo relação com a distância d do centro à reta.
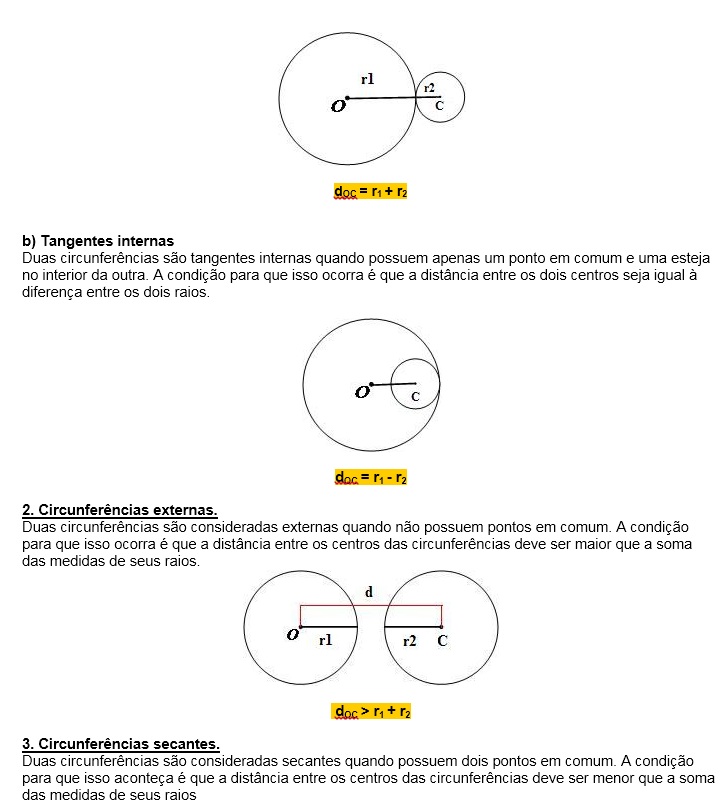
Posições relativas entre duas circunferências Matemática Enem
Olá!Nesta aula, eu mostro as três possíveis posições relativas entre uma reta e uma circunferência. Para saber qual a posição de um ponto em relação à circun. 3º caso: A reta s é secante à circunferência. Nesse caso, a distância entre o centro O e a reta s é menor que a medida do raio. Ou seja: dO,s < r. Exemplo 1. Verifique a posição relativa entre a reta s: 3x + y - 13 = 0 e a circunferência de equação (x - 3) 2 + (y - 3) 2 = 25.




