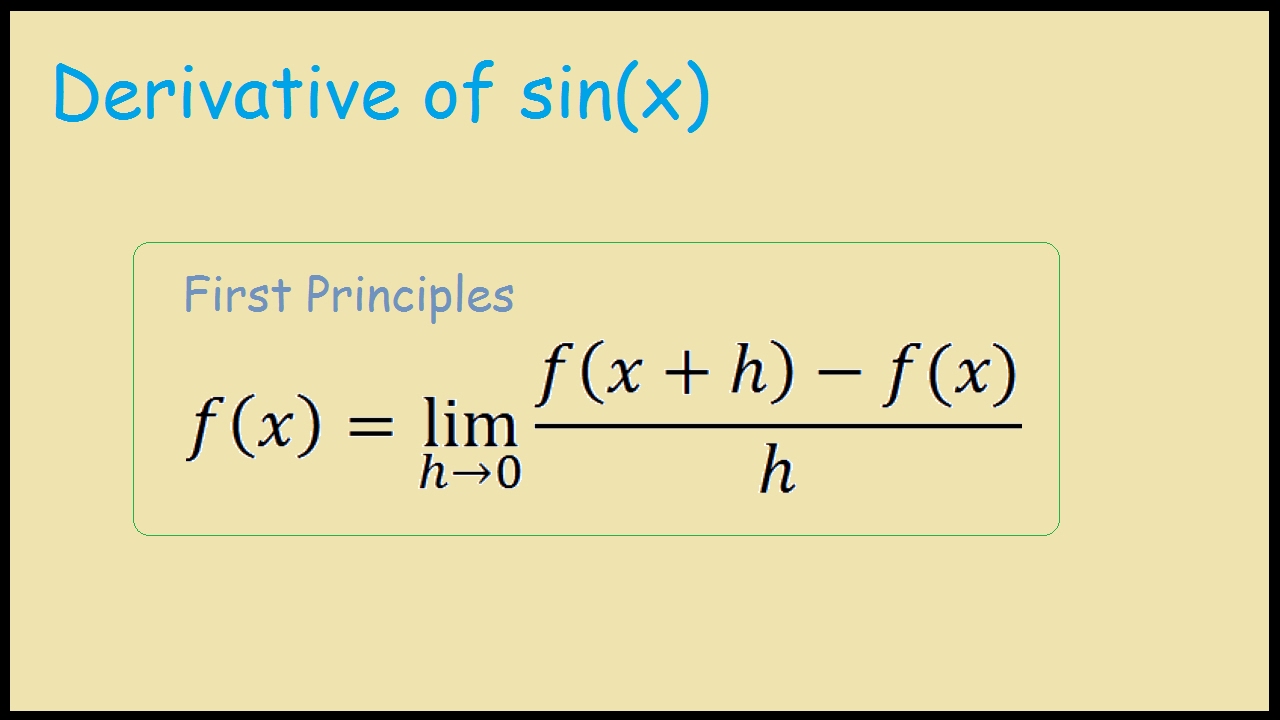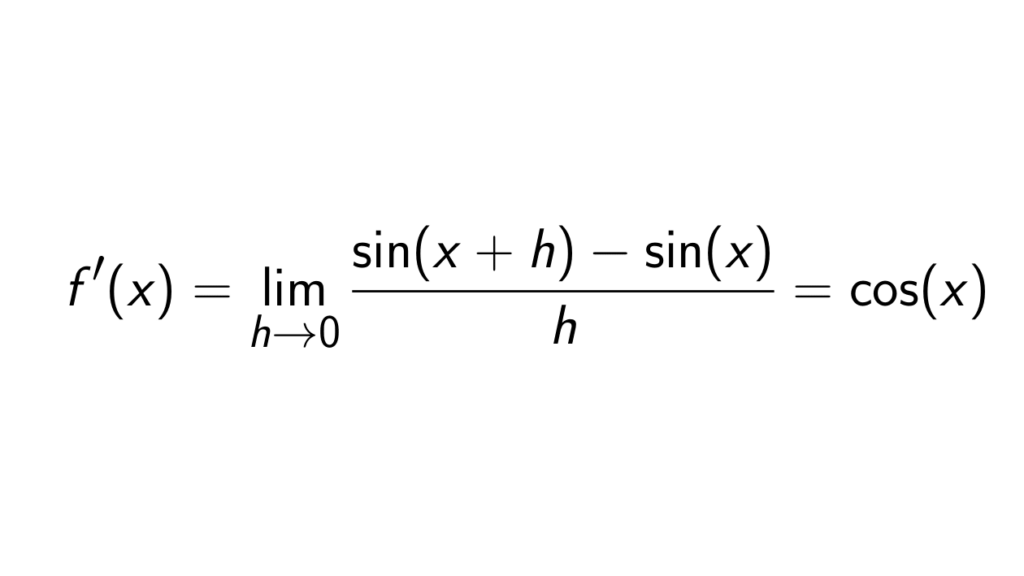Free derivative calculator - differentiate functions with all the steps. Type in any function derivative to get the solution, steps and graph The Derivative Calculator lets you calculate derivatives of functions online — for free! Our calculator allows you to check your solutions to calculus exercises. It helps you practice by showing you the full working (step by step differentiation).

Calculus Differentiation Derivative of Sin x from first principle
Given a function , there are many ways to denote the derivative of with respect to . The most common ways are and . When a derivative is taken times, the notation or is used. These are called higher-order derivatives. Note for second-order derivatives, the notation is often used. At a point , the derivative is defined to be . Sign in Free simplify calculator - simplify algebraic expressions step-by-step How do you find the derivative of 1 sin x? Calculus Differentiating Trigonometric Functions Differentiating sin (x) from First Principles 1 Answer Steve M Nov 10, 2016 d dx ( 1 sinx) = − cotxcscx Explanation: There are several methods to do this: Let y = 1 sinx ( = cscx) Method 1 - Chain Rule Rearrange as y = (sinx)−1 and use the chain rule: Example 3.5.2: Finding the Derivative of a Function Containing cos x. Find the derivative of g(x) = cosx 4x2. Solution. By applying the quotient rule, we have. g′ (x) = ( − sinx)4x2 − 8x(cosx) (4x2)2. Simplifying, we obtain. g′ (x) = − 4x2sinx − 8xcosx 16x4 = − xsinx − 2cosx 4x3.
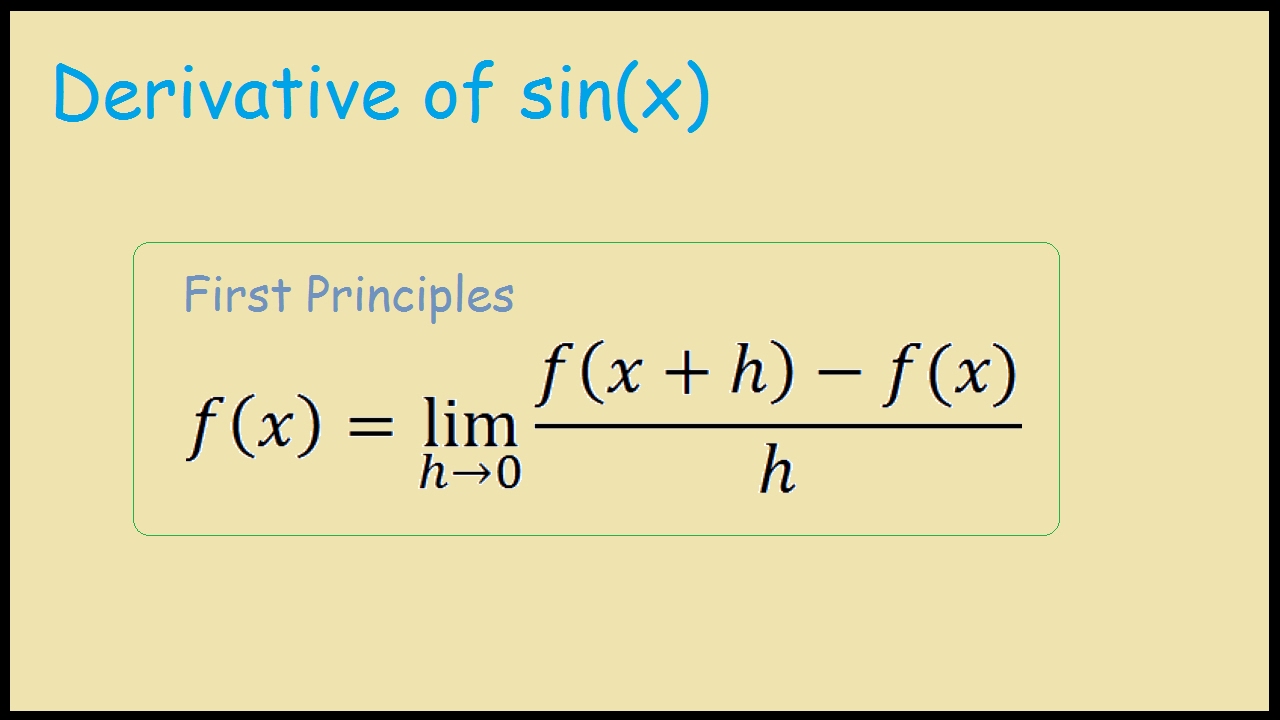
Derivative of Sin(x) from first principles YouTube
Derivative of sin(x) Save Copy. Log InorSign Up. f x = sin x. 1. a, f a. 2. a = 0. 0 1 4. 3. g x = d dx. derivative of 1/sinx Natural Language Math Input Extended Keyboard Examples Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music… Derivatives of the Sine and Cosine Functions. We begin our exploration of the derivative for the sine function by using the formula to make a reasonable guess at its derivative. Recall that for a function f(x), f ′ (x) = lim h → 0f(x + h) − f(x) h. Consequently, for values of h very close to 0, f ′ (x) ≈ f ( x + h) − f ( x) h. Step 1: d dx{sinx} |x = 0. By definition, the derivative of sinx evaluated at x = 0 is. d dx{sinx} |x = 0 = lim h → 0 sinh − sin0 h = lim h → 0sinh h. We will prove this limit by use of the squeeze theorem (Theorem 1.4.18). To get there we will first need to do some geometry.
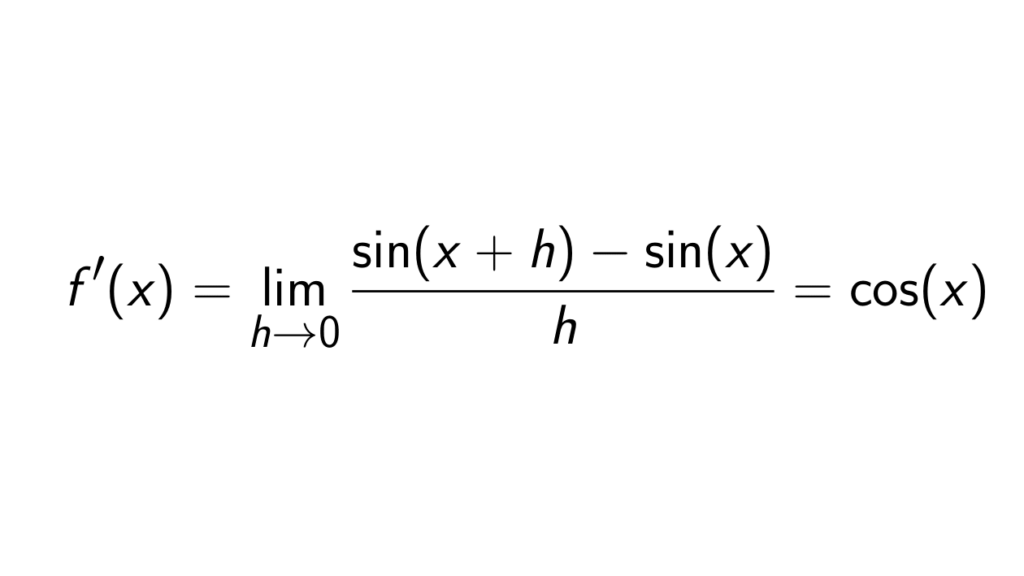
Derivative of sin(x) using First Principle of Derivatives Epsilonify
AboutTranscript. Now we explore the intuition behind the derivatives of trigonometric functions, discovering that the derivative of sin (x) is cos (x) and the derivative of cos (x) is -sin (x). By analyzing tangent line slopes, we gain a deeper understanding of these fundamental relationships. Differentiate. Tap for more steps. (1−sin(x))cos(x)+(1+sin(x)) d dx [sin(x)] (1−sin(x))2 ( 1 - sin ( x)) cos ( x) + ( 1 + sin ( x)) d d x [ sin ( x)] ( 1 - sin ( x)) 2 The derivative of sin(x) sin ( x) with respect to x x is cos(x) cos ( x).
Google Classroom. Proving that the derivative of sin (x) is cos (x) and that the derivative of cos (x) is -sin (x). The trigonometric functions sin ( x) and cos ( x) play a significant role in calculus. These are their derivatives: d d x [ sin ( x)] = cos ( x) d d x [ cos ( x)] = − sin ( x) The AP Calculus course doesn't require knowing the. The rules for derivatives that we have are no help, since sin x is not an algebraic function. We need to return to the definition of the derivative, set up a limit, and try to compute it. Here's the definition: (4.2.1) d d x sin x = lim Δ x → 0 sin ( x + Δ x) − sin x Δ x. Using some trigonometric identities, we can make a little progress.

Example 16 Compute derivative of sin x Chapter 13 Class 11
Derivative of Sin x Examples. Example 1: Find the derivative of sin (x+1), with respect to x, using the first principle. Solution: Assume that f(x) = sin (x+ 1). Now, we have to find the derivative of sin (x+1), using the 1st principle. Here are some important points to note from the differentiation of sin x. The derivative of sin x with respect to x is cos x. The derivative of sin u with respect to x is, cos u · du/dx. Sin x is maximum at x = π /2, 5π/2,.. and minimum at x = 3π/2, 7π/2,. At all these points, the derivative of sin x is 0.