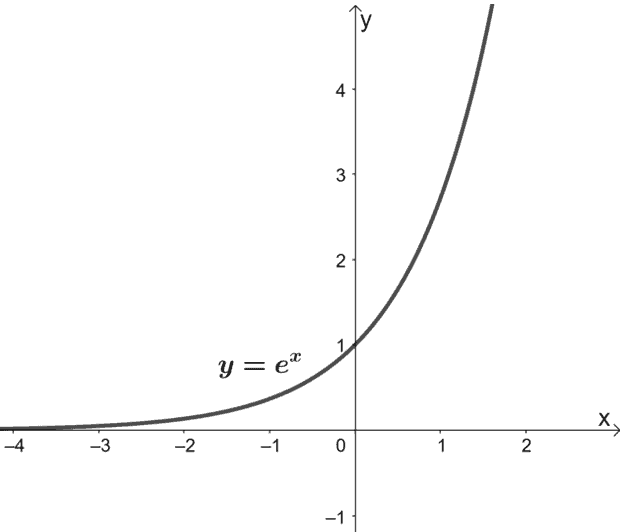
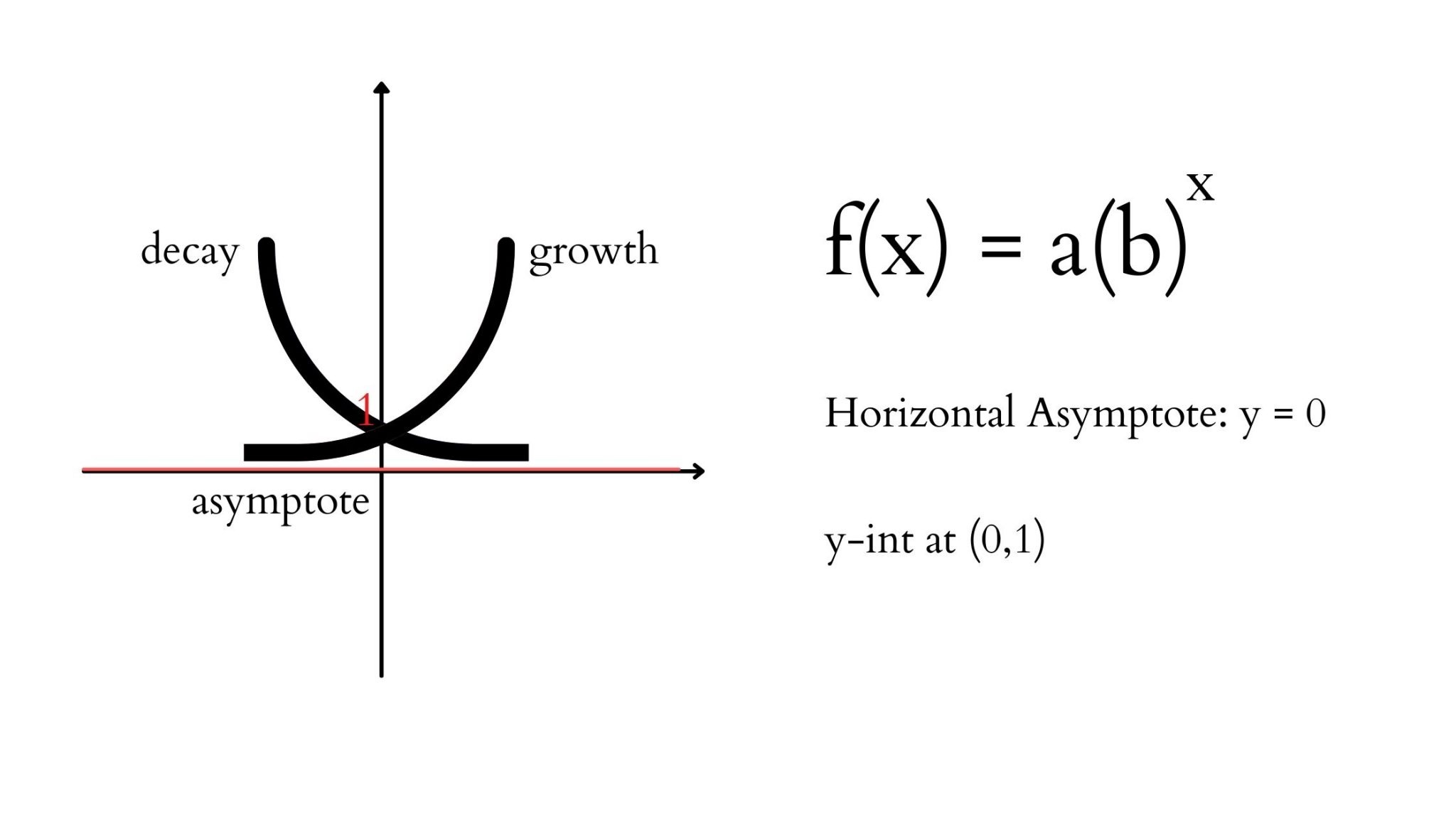
Exponential functions are one-to-one functions. • graph crosses the y -axis at (0,1) • when b > 1, the graph increases • when 0 < b < 1, the graph decreases • the domain is all real numbers • the range is all positive real numbers (never zero) • graph passes the vertical line test for functions This is a parent function for the exponential function. The "2" is called the base; an exponential function can have any number as its base.. Exponential functions do not have vertices, but they do have a horizontal asymptote: a horizontal line which the graph will get very, very close to. 3. Pay close attention to the key points: x- and y.
Parent Functions Types, Properties & Examples
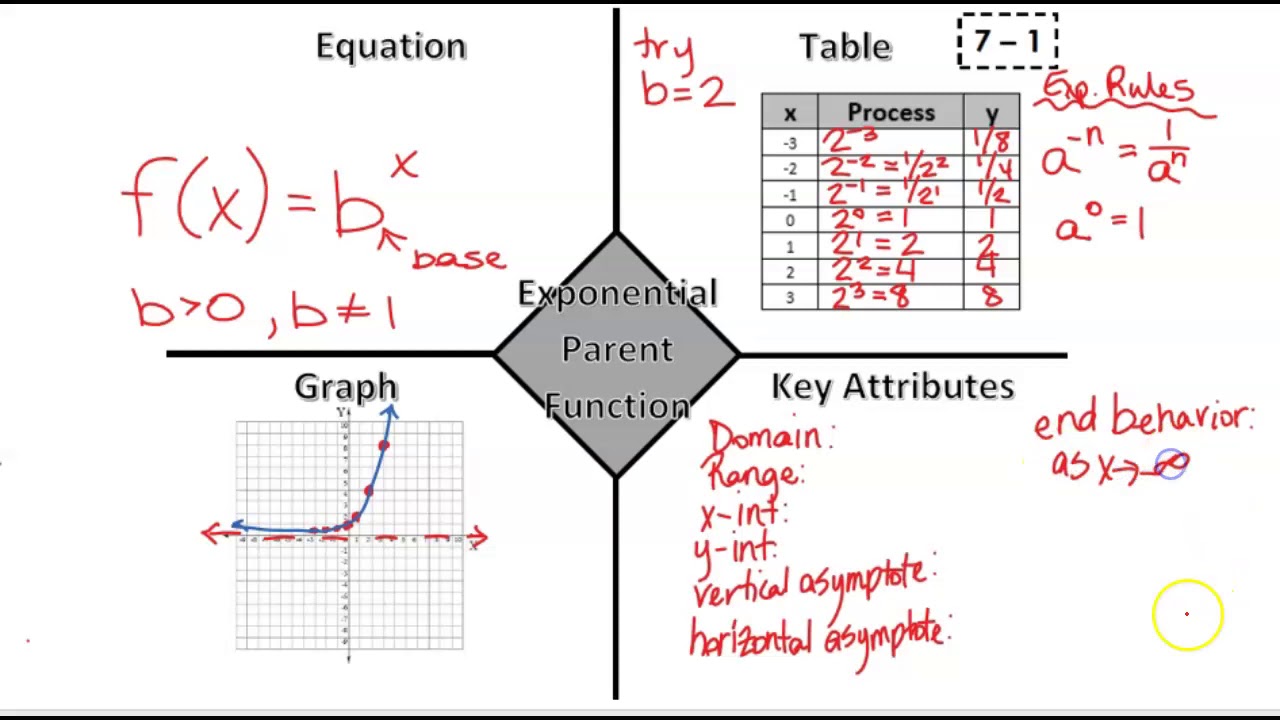
An exponential function represents the relationship between an input and output, where we use repeated multiplication on an initial value to get the output for any given input. Exponential functions can grow or decay very quickly. Graph Basic Exponential Functions. Exponential growth is modelled by functions of the form f(x) = bx where the base is greater than one. Exponential decay occurs when the base is between zero and one. We'll use the functions f(x) = 2x and g(x) = (1 2)x to get some insight into the behaviour of graphs that model exponential growth and decay. Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form f(x) = bx whose base is greater than one. We'll use the function f(x) = 2x . Observe how the output values in Table 4.3.1 change as the input increases by 1. Table 4.3.1. The domain of f(x) = 2x is all real numbers, the range is (0, ∞), and the horizontal asymptote is y = 0. To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form f(x) = bx whose base is between zero and one. We'll use the function g(x) = (1 2)x.
PPT Parent Functions PowerPoint Presentation, free download ID2576658
Unit 1 Polynomial arithmetic Unit 2 Complex numbers Unit 3 Polynomial factorization Unit 4 Polynomial division Unit 5 Polynomial graphs Unit 6 Rational exponents and radicals Unit 7 Exponential models Unit 8 Logarithms Unit 9 Transformations of functions Unit 10 Equations Unit 11 Trigonometry Unit 12 Modeling Course challenge Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Graphing exponential functions (parent functions) - YouTube © 2023 Google LLC We'll build a simple table of values and then graph y = 2^x and then y = (1/2)^2, which are the basic exponential.
71 Exponential Parent Function YouTube
A parent function represents a family of functions' simplest form. This definition perfectly summarizes what parent functions are. We use parent functions to guide us in graphing functions that are found in the same family. In this article, we will: Review all the unique parent functions (you might have already encountered some before). 8. Table 1. Each output value is the product of the previous output and the base, 2. We call the base 2 the constant ratio. In fact, for any exponential function with the form f (x) = ab is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output.
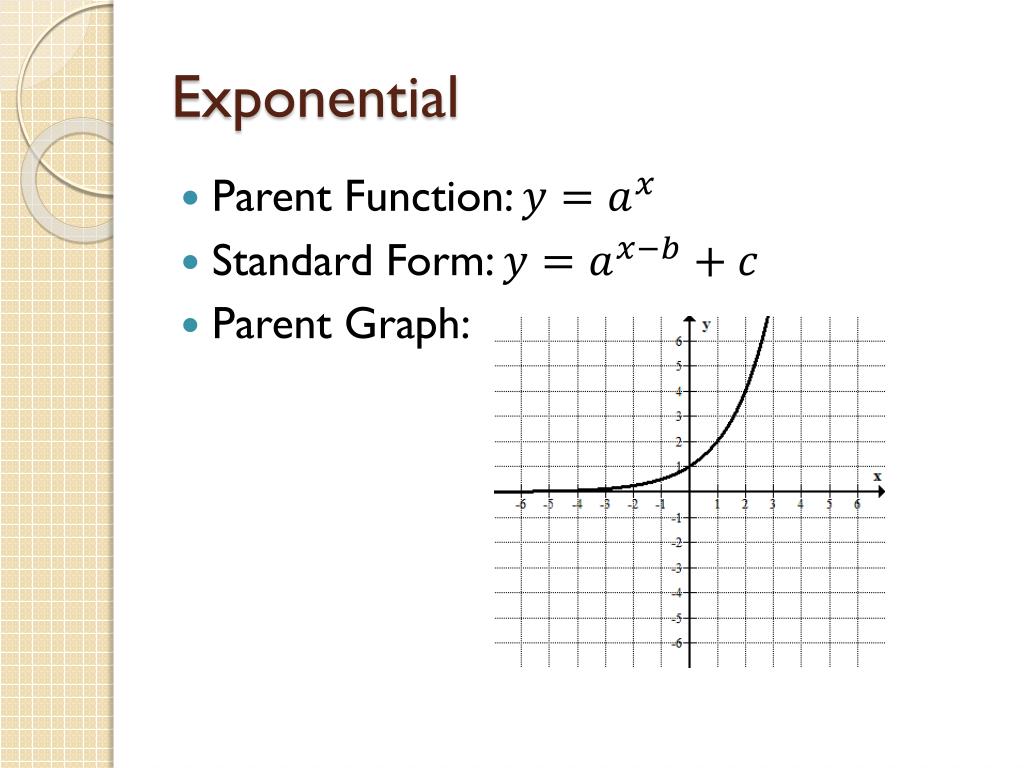
Definition: A parent function is the most basic function from which a family of similar functions is derived. By performing various operations like addition, subtraction, multiplication, etc. on a parent function you obtain a function that belongs to the same family. Parent function graphs are the graphs of the respective parent function. Custom Solutions Log In Exponential functions follow all the rules of functions. However, because they also make up their own unique family, they have their own subset of rules. The fo
Exponential Functions. Transformations and Applications IntoMath
What is a Parent Function? In mathematics, functions are defined as a relationship between input (independent variable such as x) and an output (dependent variable such as y). This relationship. Linear Parent Function Equation: y = x Domain: All real numbers Range: All real numbers Slope of the line: m = 1 Y-intercept: (0,0) 03 of 09 Quadratic Parent Function Equation: y = x 2 Domain: All real numbers




