1 Factoring Flow Chart Download 2 More Resources for Teaching Quadratics Today I'm sharing a factoring flow chart that has been really helpful to my students. Factoring finally clicked for my college algebra students. It was definitely a Hallelujah! moment. The lowest grade on the factoring test was a 95. The flow chart on the first page gives you a quick reference on approaching a factoring problem. Complex factoring problems can be solved using the chart as a general guide and applying the techniques that will be discussed below. As with any concept, the way to get good at factoring is to practice it a lot.
Factoring Polynomials (Flowchart with Examples)
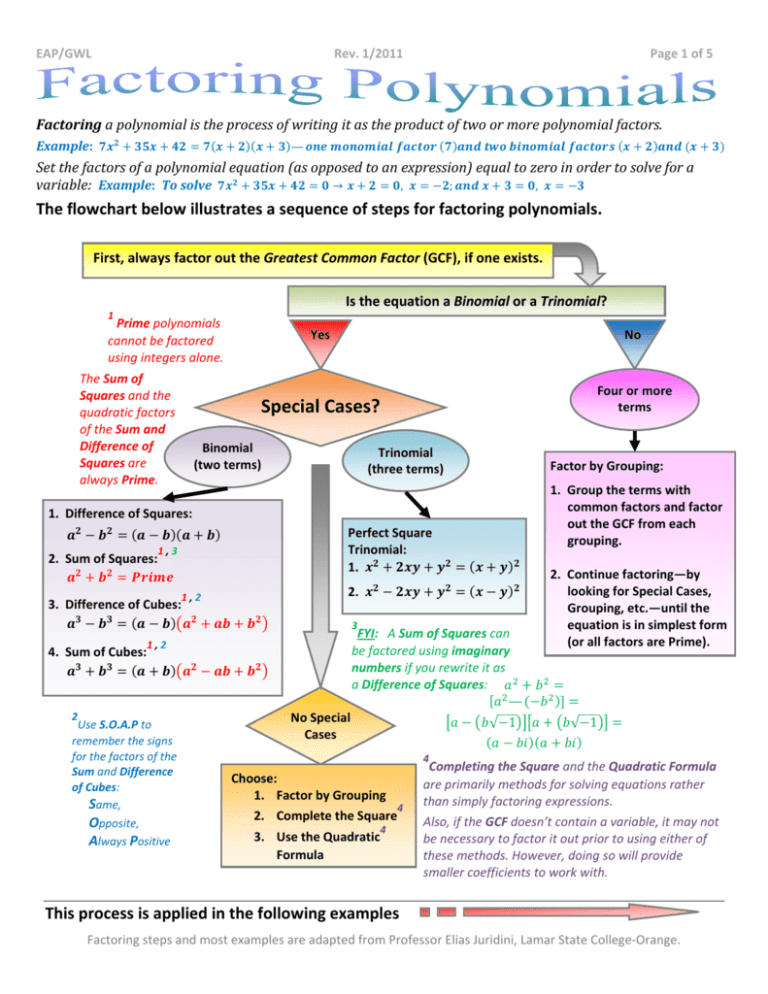
Start Is there a common factor? Yes How many terms are there? Factor out the GCF Three Factor into two Binomials ( )( Examples: 2 xx− 4 xx− 21 = (xx− 2 10 xx + 11 xx + 3 = (2 xx + Four Factor by Grouping Example: 3 = 2 aa(3 矎뇿 + 1) +3(3矎뇿 +1)矎뇿 By Difference of Squares +1)(2 aa +3) Here's a handy dandy flow chart to help you calculate limits. Key point #1: Direct substitution is the go-to method. Use other methods only when this fails, otherwise you're probably doing more work than you need to be. Factoring Flow Chart Factor out the Greatest Common Factor (GCF): Ex: 2 2 + 6 → GCF = 2 Once we factor out the GCF = 2 , we're left with ( + 3). 2 2 + 6 = 2 ( + 3) Start Here! How many terms 2 are in your polynomial? 3 Factor by Grouping: Group in groups of two terms Ex: → factor GCF Factoring Flowchart Start No Is there a common factor? Yes How many terms are there? Factor out the GCF Two Three Four Is it a Difference of Squares? 2 − 2 = ሺ⬚ ሻሺ⬚ሻ Examples: 2 − 4 10 2 − 11 − 21 = ሺ − 7ሻሺ + 3ሻ − 3 = ሺ2 − 1 ሻሺ5 + 3ሻ ሺ− ሻ ሺ + 2 − 25 = ሺ − 5ሻሺ + 5ሻ 9 2 − 64 = ሺ3 − 8 ሻሺ3 + 8ሻ By Difference of Squares Example: 2 − 10 + 25 − 2
Factoring Flow Chart
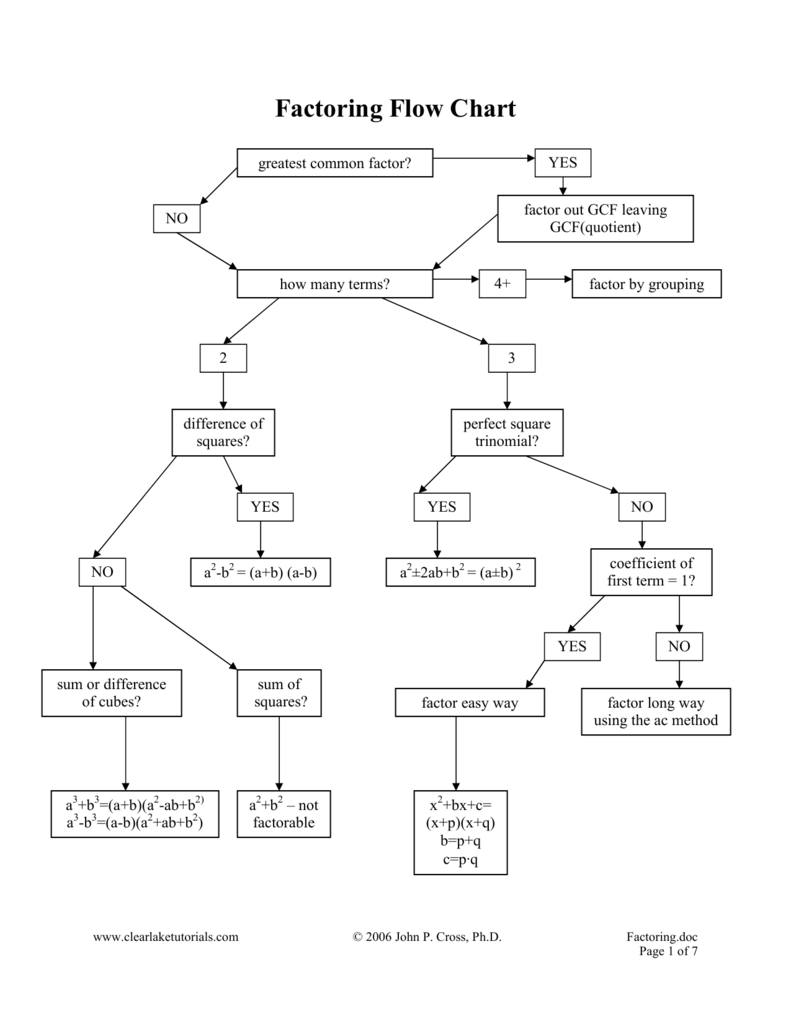
Factoring Flow Chart . M-F7. Perfect Square (See M-F3) (See M-F3) iiiiaa Binomial 2 Terms Perfect Cube Trinomial 3 Terms Polynomial With 4 Terms Factor by Grouping (See M-FI) Group the first two terms together and the last two terms together. Then factor the GCF out of each group. Example: 8x2- 12x+ IOx— 15 (8x2- 12x) + (lox - 15) Unit 1 Polynomial arithmetic Unit 2 Complex numbers Unit 3 Polynomial factorization Unit 4 Polynomial division Unit 5 Polynomial graphs Unit 6 Rational exponents and radicals Unit 7 Exponential models Unit 8 Logarithms Unit 9 Transformations of functions Unit 10 Equations Unit 11 Trigonometry Unit 12 Modeling Course challenge Factor out what is common. YES YES NO Are there 2, 3, or 4 terms in the expression? Is it a difference of squares a2 −b pattern? Factor according to the pattern ()( )a +b a −b. "the parentheses match, except one's a plus and one's a minus." 2 Is it a sum or cubes a3 +b3 or a3 −b3 pattern? NO Factor according to the pattern ()a+b. This video was created using #Keynote to provide students with an animated version of a static flow chart for factoring polynomials. Consider using both the.
Factoring Flow Chart Math = Love
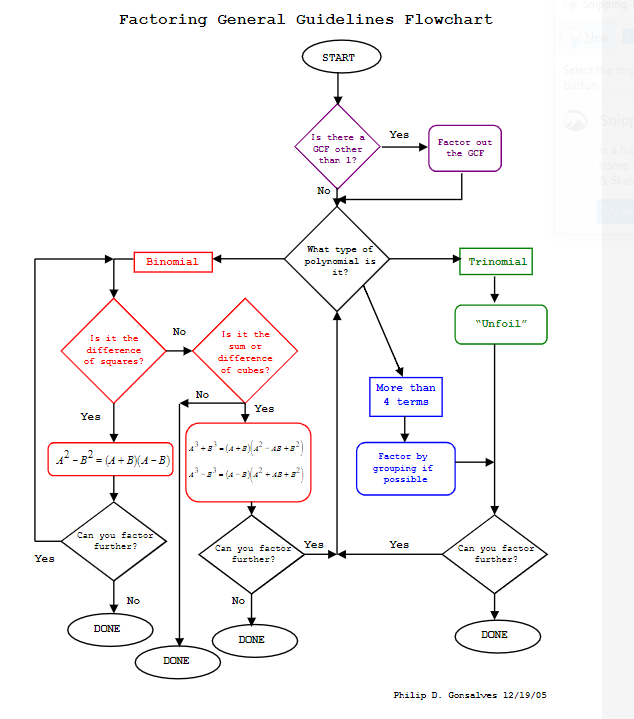
Factoring Flowchart Factoring Flowchart OR Trial and Error REMEMBER Always factor completely. After any step of factoring, look at each new factor to see if you can factor it any further. Check you answers. Multiplying your answers out using distribution. Factoring Flow Chart for: ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) Factoring Flow Chart for: Author: e127096 Created Date: 2/28/2013 7:53:12 PM
Factoring Flow Chart Quadratics: ax 2 bx c Start: Can you factor out a common term? yes Can you factor what is left? no DONE no yes DONE Is it a difference of squares? ( x 2 a 2 ) yes no Factor to ( x a )( x a ) . Is the coefficient on the x 2 term one? DONE yes no Find the factors of c that add up to b. Start Is there a GCF? Factor out The GCF No Two How many terms do you have? Four Which special type is it? Factor by grouping, Usually 2 by 2, Sometimes 3 by 1 Three What is the Value of in a a ≠ 1 Difference of Cubes A 3 − B 3 ( 2 A − B )( A + AB + 2 B ) Sum of Cubes ax 2 + bx + c ? 3 3 A + B Find factors of ac To the value of .
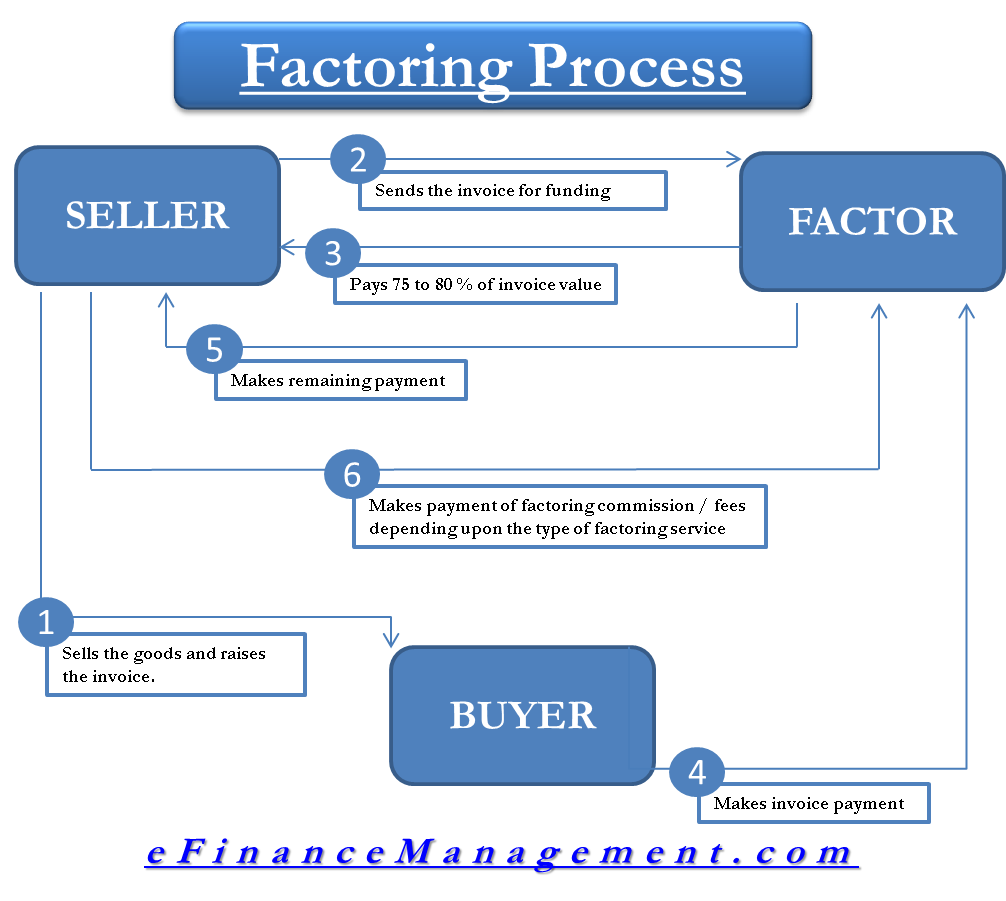
Factoring Definition, Concept, Types, Functions, Process, Pros and Cons
yes no Note: If you tried all the factor pairs, and none sum to b, it can't be factored! Difference of Squares a2 - b2 = (a-b)(a+b) Trinomial where a = 1 Find factors of c that add to b. Trinomial where a 1 Find factors of ac that add to b. Split the middle term and then factor by grouping. Use this handy flow chart when choosing the correct method when factoring a quadratic expression.




