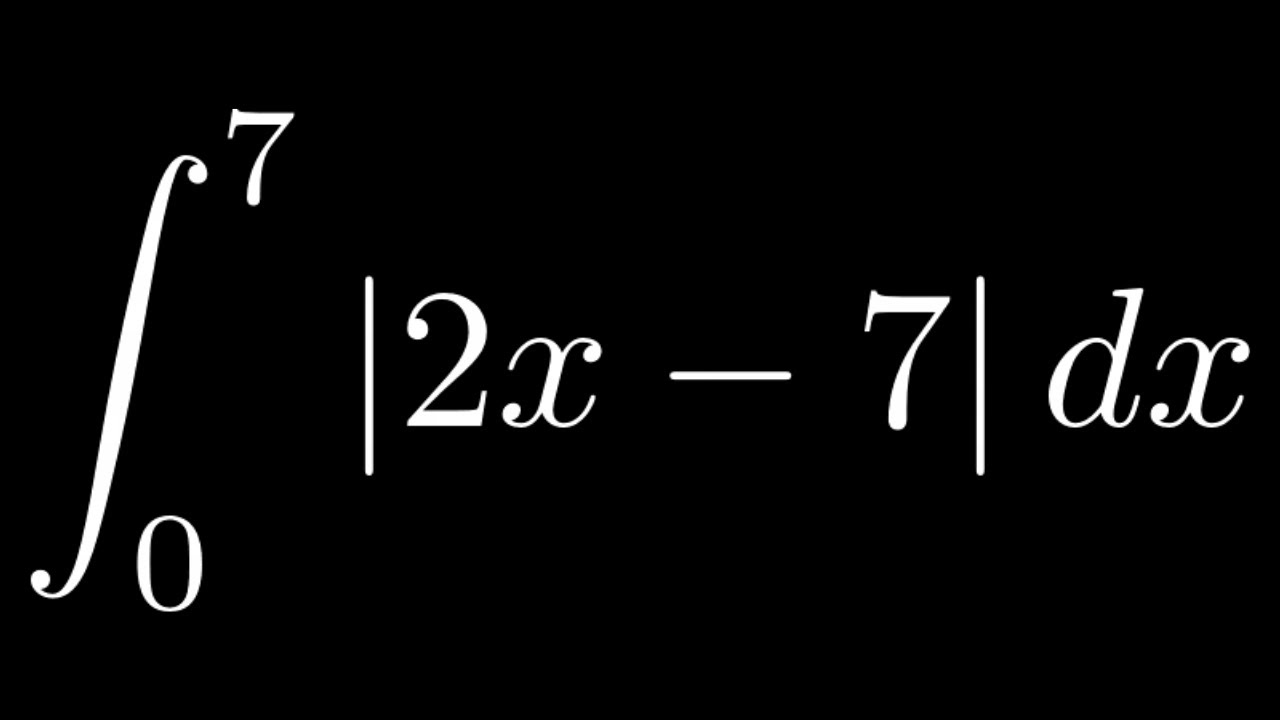Get thousands of teacher-crafted activities that sync up with the school year. Access the most comprehensive library of K-8 resources for learning at school and at home. Definite integral of absolute value function (video) | Khan Academy AP®︎/College Calculus AB Course: AP®︎/College Calculus AB > Unit 6 Lesson 10: Finding antiderivatives and indefinite integrals: basic rules and notation: definite integrals Definite integral involving natural log Definite integrals: common functions

Evaluating the integral of an absolute value function YouTube
The integral of an absolute value function is an integral where the integrand is an absolute value function. But what is an absolute value function? It's pretty simple: An absolute value function is a function in which the variable is inside the absolute value bars. Integrating an Absolute Value Z 4 jx3 5x2 + 6xj dx 0 There is no anti-derivative for an absolute value; however, we know it's de nition. jxj = x if x 0 x elsewise Thus we can split up our integral depending on where x3 5x2 + 6x is non-negative. x3 5x2 + 6x 0: x(x2 5x + 6) 0: x(x 2)(x 3) 0: After testing the intervals (1 ; Free integral calculator - solve indefinite, definite and multiple integrals with all the steps. Type in any integral to get the solution, steps and graph Integral of absolute value of x or abs (x) The Organic Chemistry Tutor 7.27M subscribers Subscribe Subscribed 185K views 5 years ago Basic Integration This calculus video tutorial explains how.

Find the Definite Integral of an Absolute Value Function Calculus YouTube
1 To expand on @davin's comment: Use the definition of the absolute value! The absolute value equals "the inside" when "the inside" is non-negative, and equals " (-) the inside" when "the inside is negative. Using the Fundamental Theorem of Calculus to evaluate this integral with the first anti-derivatives gives, ∫ 2 0 x2 +1dx = (1 3 x3 +x)∣∣ ∣2 0 = 1 3(2)3 +2 −( 1 3(0)3 +0) = 14 3 ∫ 0 2 x 2 + 1 d x = ( 1 3 x 3 + x) | 0 2 = 1 3 ( 2) 3 + 2 − ( 1 3 ( 0) 3 + 0) = 14 3 Much easier than using the definition wasn't it? Definite Integral with Absolute Value (Example) James Elliott 9.41K subscribers Subscribe Subscribed 51K views 2 years ago Various Integration Videos This video works through an example of. integral of absolute value function Natural Language Math Input Extended Keyboard Examples Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music…

Question Video Evaluating the Definite Integral of an Absolute Value
Keywords👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiati. Video Transcript. If 𝑓 of 𝑥 is equal to six times the absolute value of 𝑥, determine the integral from negative six to six of 𝑓 of 𝑥 with respect to 𝑥. In this question, we're asked to evaluate the definite integral of six times the absolute value of 𝑥. And we know a few different ways for evaluating a definite integral.
Video Transcript. Evaluate the definite integral between negative four and five of the absolute value of 𝑥 minus two with respect to 𝑥. For this question, we've been asked to evaluate the definite integral of a function, which we'll call lowercase 𝑓. This function is the absolute value or the modulus of 𝑥 minus two. Integrals of Absolute Value Functions Practice Problems 1) ∫3 0 |x − 2| dx Show Answer 2) ∫6 0 |2x − 4| dx Show Answer 3) ∫4 0 |x + 3| dx Show Answer 4) ∫4 0 |3x − 6| dx Show Answer 5) ∫4 −4 |x| dx Show Answer 6) ∫3 0 |x + 1| dx Show Answer 7) ∫4 −1 |3x − 5| dx Show Answer 8) ∫2 −1 |5 − x| dx Show Answer 9) ∫−3 −7 −|x + 5| dx Show Answer
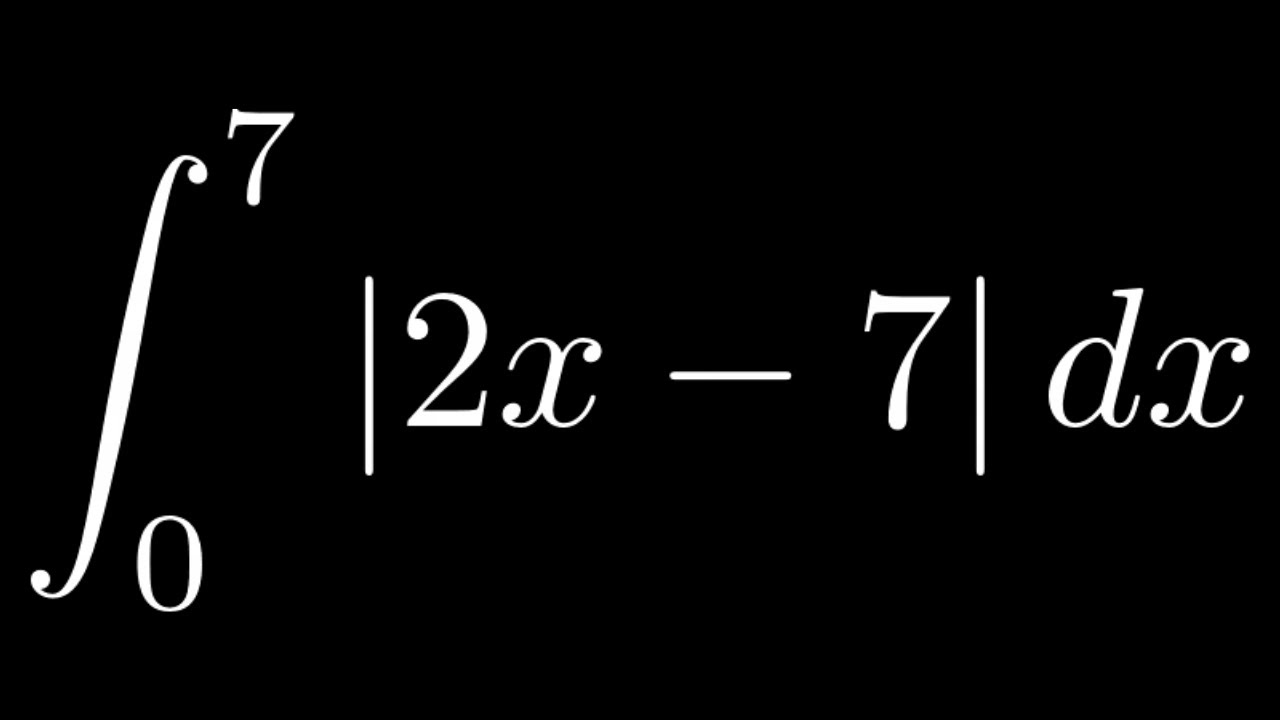
Definite Integral with Absolute Value 2x 7 from 0 to 7/2 YouTube
Step 1 : To evaluate the integral, we first equate the given function to zero and find x intercept. Step 2 : The modulus function will always have the shape of V. Draw the graph. Step 3 : With the given interval, divide the integral into parts, then integrate it. Problem 1 : Solution : Let y = 5x-3 put y = 0 5x-3 = 0 x = 3/5 In this video I explained how to integrate a function with argument containing absolute values.