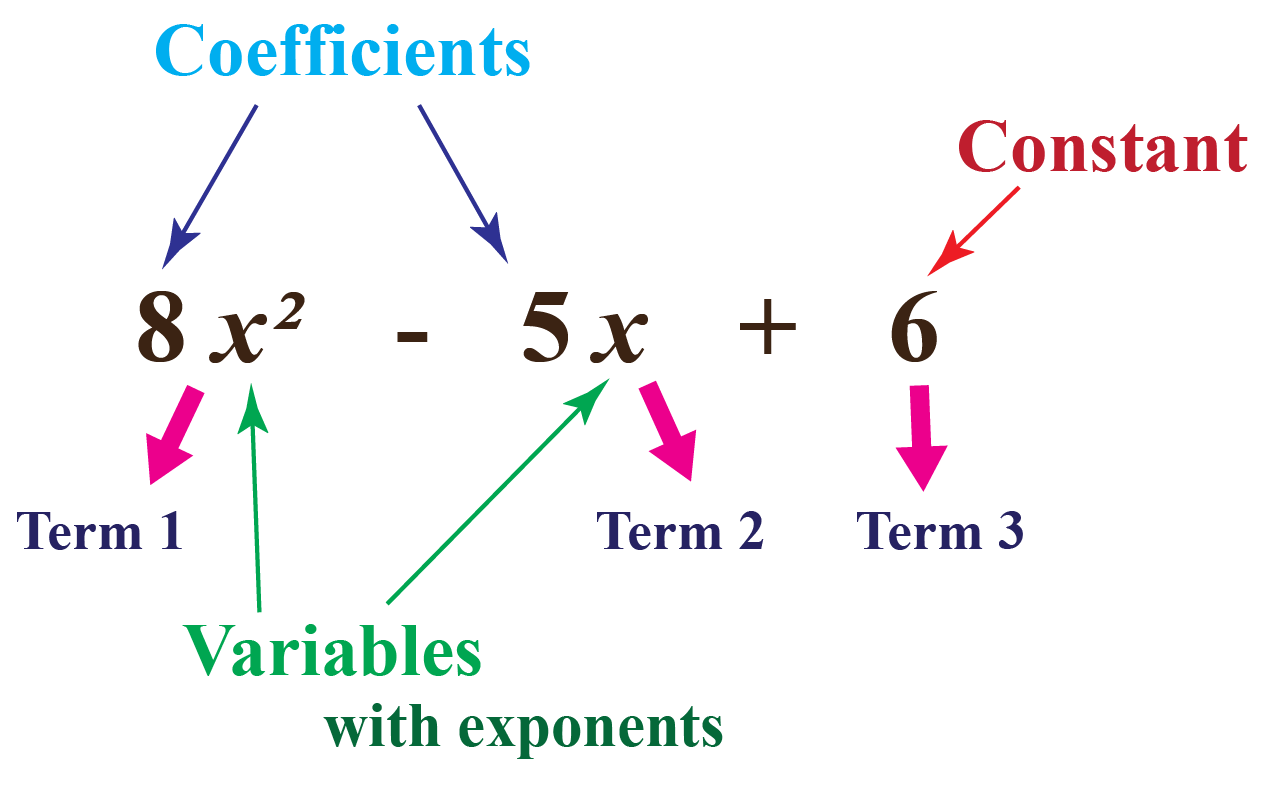The standard form of a polynomial is given by, f (x) = a n x n + a n-1 x n-1 + a n-2 x n-2 +. + a 1 x + a 0. Meaning of Polynomial in Standard Form A mathematical expression of one or more algebraic terms in which the variables involved have only non-negative integer powers is called a polynomial. A polynomial is an expression of two or more algebraic terms, often having different exponents. Adding polynomials. Read More. Save to Notebook! Sign in. Send us Feedback. Free Polynomial Standard Form Calculator - Reorder the polynomial function in standard form step-by-step.
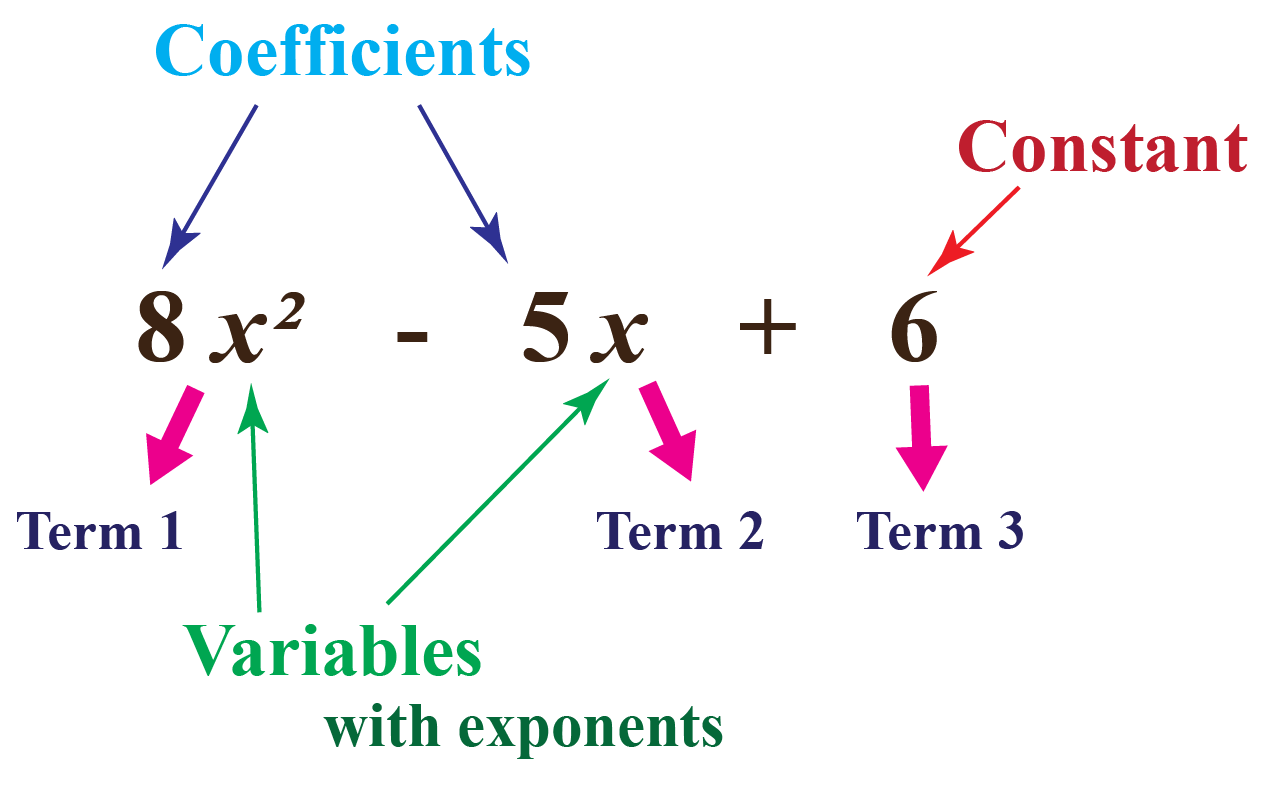
Standard Form Polynomial Cuemath
Standard form of a polynomial is a way of writing a polynomial where the terms are arranged in descending order of degree. A polynomial in standard form is a polynomial written such that its exponents are in descending order. The standard form of a polynomial with degree n is given by a n x n + a n − 1 x n − 1 + . . . + a 1 x + a 0 About Transcript This introduction to polynomials covers common terminology like terms, degree, standard form, monomial, binomial and trinomial. Polynomials are sums of terms of the form k⋅xⁿ, where k is any number and n is a positive integer. For example, 3x+2x-5 is a polynomial. Created by 1. Hello Fren. Questions Tips & Thanks To write a polynomial in standard form, you must do the following steps: Add (or subtract) the like terms of the polynomial. Write the term with the highest degree first. Write all the other terms in decreasing order of degree. Remember that a term with a variable but without an exponent is of degree 1. Answer: Refer to Explanation. Explanation: The degree of a polynomial is determined by the highest power of x in the polynomial e.g. f (x) = 2x5 − 3x2 + 4 The highest power of x in f (x) is 5. Hence, degree of f (x) = 5 A polynomial with only a constant, e.g. P (x) = 5 has a degree of 0 as 5 = 5x0 Untitled · 1 · May 4 2018

Polynomials in Standard Form YouTube
So: A polynomial can have constants, variables and exponents, but never division by a variable. Also they can have one or more terms, but not an infinite number of terms. Polynomial or Not? These are polynomials: 3x x − 2 −6y2 − ( 7 9 )x 3xyz + 3xy2z − 0.1xz − 200y + 0.5 512v5 + 99w5 5 1.41M subscribers 418K views 11 years ago End Behavior of Polynomial Functions 👉 Learn how to determine the end behavior of the graph of a polynomial function. To do this we will first need to. Solution: The first term is the one with the biggest power: \ (5x^2−9x^5+8x^3−11= −9x^5+8x^3+5x^2−11 \) Writing Polynomials in Standard Form - Example 3: Write this polynomial in standard form. \ (-12+3x^2-6x^4=\) Solution: The first term is the one with the biggest power: \ (-12+3x^2-6x^4=-6x^4+3x^2-12\) Writing Polynomials in Standard Form One way to write a polynomial is in standard form. In order to write any polynomial in standard form, you look at the degree of each term. You then write each term in order of degree, from highest to lowest, left to right. Let's look at an example. Write the expression 3 x − 8 + 4 x 5 in standard form.

PPT Introduction to Polynomials PowerPoint Presentation, free
This is called standard form. The following polynomials are in standard form: 4x4 − 3x3 + 2x2 − x + 1. a4b3 − 2a3b3 + 3a4b − 5ab2 + 2. The first term of a polynomial in standard form is called the leading term, and the coefficient of the leading term is called the leading coefficient. The "Standard Form" for writing down a polynomial is to put the terms with the highest degree first (like the "2" in x 2 if there is one variable). Example: Put this in Standard Form: 3 x2 − 7 + 4 x3 + x6 The highest degree is 6, so that goes first, then 3, 2 and then the constant last: x6 + 4 x3 + 3 x2 − 7 Standard Form of a Linear Equation
Evaluate the following statement: The degree of a polynomial in standard form is the exponent of the leading term. Explain why the statement is true or false. 2. Many times, multiplying two binomials with two variables results in a trinomial. This is not the case when there is a difference of two squares. 1) Write the term with the highest exponent first. 2) Write the terms with lower exponents in descending order. 3) Remember that a variable with no exponent has an understood exponent of 1. 4) A constant term (a number with no variable) always goes last. Here's a few examples: 1) 6y3+4y5-2y2-6y+8y4+7. The highest exponent is the 5, so that.

Standard form of a polynomial Standard form, Polynomials, Combining
Solution: The third expression (-21x 5 + 3x 3 - 99) is in standard form because it is written in order of degree, Example question #2: Write the following polynomial in standard form and classify the expression by degree: 3x 2 - 7x 4 + 38 + 4x. Solution: Step 1: Write the degree of each term: 3x 2 = 2nd degree. - 7x 4 = 4th degree. Standard Form of a Polynomial The general form to represent the polynomial is as follows: \ (\begin {array} {l}F (x)= a_ {n}x^ {n} + a_ {n-1}x^ {n-1} + a_ {n-2}x^ {n-2} +.+a_ {1}x+a_ {0}\end {array} \) Here, a 0 ,….a n is a constant x is a variable Types of Polynomial The different types of polynomial expressions are: