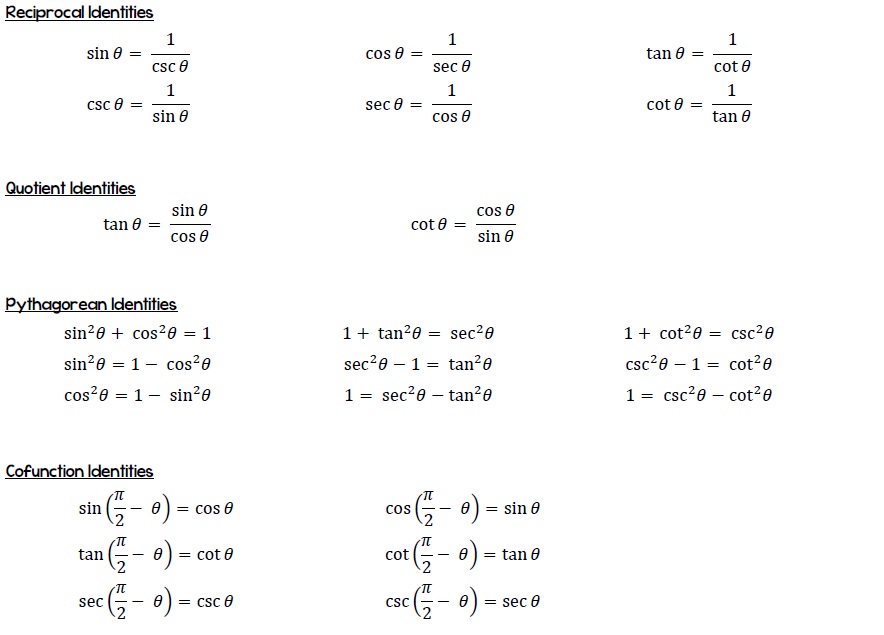21 Trig Identities Every Calculus Student Should Know! { 6. sin 1 = csc 2 1 csc cos 1 = sin . p 3 = sec Two Special Triangles sec = cos tan 7.{ 8. sin = cos cot 9. sin2 + cos2 10. 11. 12. sin( cos = sin 1 = cot 2 1 = tan = 1 (Pythagorean Identity) . 1 tan2 + 1 = sec2 cot2 1 = csc2 ) = sin 13. 14. sin( cos( cos Trigonometric identities like sin²θ+cos²θ=1 can be used to rewrite expressions in a different, more convenient way. For example, (1-sin²θ) (cos²θ) can be rewritten as (cos²θ) (cos²θ), and then as cos⁴θ. Created by Sal Khan. Questions Tips & Thanks Want to join the conversation? Sort by: Top Voted E Man 9 years ago
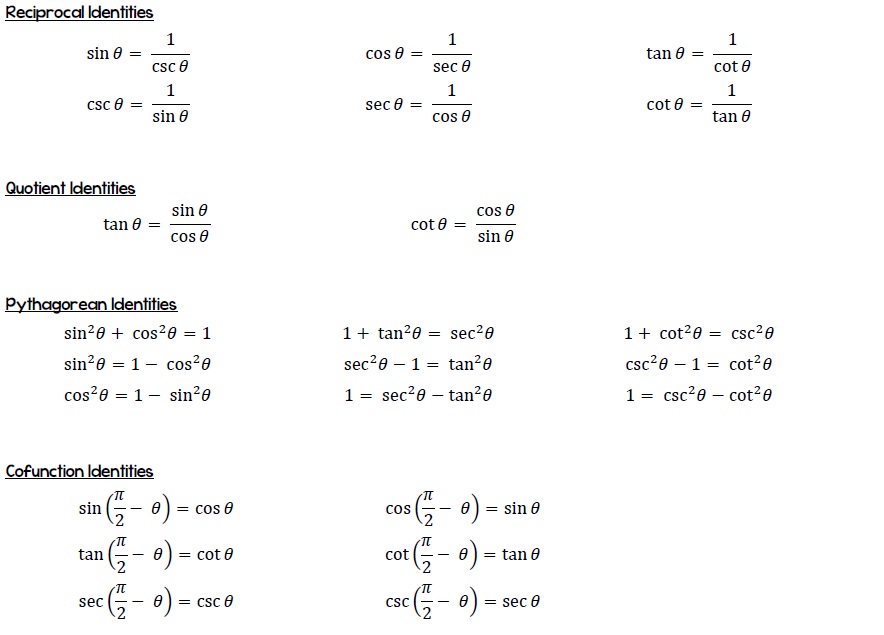
Trig Identities AP Calculus AB & BC
From this right triangle we get the following definitions of the six trig functions. Remembering both the relationship between all six of the trig functions and their right triangle definitions will be useful in this course on occasion. Next, we need to touch on radians. 7 years ago. The easiest way is to see that cos 2φ = cos²φ - sin²φ = 2 cos²φ - 1 or 1 - 2sin²φ by the cosine double angle formula and the Pythagorean identity. Now substitute 2φ = θ into those last two equations and solve for sin θ/2 and cos θ/2. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. Trigonometric Identities Purplemath What is an identity? In mathematics, an "identity" is an equation which is always true, regardless of the specific value of a given variable. An identity can be "trivially" true, such as the equation x = x or an identity can be usefully true, such as the Pythagorean Theorem's a2 + b2 = c2 MathHelp.com

The Pythagorean Identities for Trigonometric Functions YouTube
You'll learn how to use trigonometric functions, their inverses, and various identities to solve and check equations and inequalities, and to model and analyze problems involving periodic motion, sound, light, and more. Inverse trigonometric functions Learn Intro to arcsine Intro to arctangent Intro to arccosine Write the basic trigonometric identities Radian Measure To use trigonometric functions, we first must understand how to measure the angles. Although we can use both radians and degrees, radians are a more natural measurement because they are related directly to the unit circle, a circle with radius 1. In our example of equation (1) we might begin with the expression tan2(x) + 1 tan 2 ( x) + 1. Example 4.1.1 4.1. 1: Verifying a Trigonometric Identity. To verify that equation (1) is an identity, we work with the expression tan2(x) + 1 tan 2 ( x) + 1. It can often be a good idea to write all of the trigonometric functions in terms of the cosine. To sum up, only two of the trigonometric functions, cosine and secant, are even. The other four functions are odd, verifying the even-odd identities. The next set of fundamental identities is the set of reciprocal identities, which, as their name implies, relate trigonometric functions that are reciprocals of each other. (Table \(\PageIndex{3}\)).

Trig Identities Study Sheet
The Essential Trigonometric Identities. Fortunately, you do not have to remember absolutely every identity from Trig class. Below is a list of what I would consider the essential identities. 1. Quotient Identities. The quotient identities are useful for re-expressing the trig functions in terms of sin and/or cos. 2. Trig identities are trigonometry equations that are always true, and they're often used to solve trigonometry and geometry problems and understand various mathematical properties. Knowing key trig identities helps you remember and understand important mathematical principles and solve numerous math problems. The 25 Most Important Trig Identities
TrigFormulas.dvi MATH 10560: CALCULUS II TRIGONOMETRIC FORMULAS Basic Identities The functions cos(θ) and sin(θ) are defined to be the x and y coordinates of the point at an angle of θ on the unit circle. Therefore, sin(−θ) = − sin(θ), cos(−θ) = cos(θ), and sin2(θ) + cos2(θ) = 1. Note that the three identities above all involve squaring and the number . You can see the Pythagorean-Thereom relationship clearly if you consider , where the angle is , the "opposite" side is the "adjacent" side is , and the hypotenuse is. We have additional identities related to the functional status of the trig ratios: Notice in particular.

Trig Identities All List of Trigonometric Identities Learn
What are Trigonometric Identities? Trigonometric Identities are the equalities that involve trigonometry functions and holds true for all the values of variables given in the equation. There are various distinct trigonometric identities involving the side length as well as the angle of a triangle. Algebra (all content) 20 units · 412 skills. Unit 1 Introduction to algebra. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs. Unit 4 Sequences. Unit 5 System of equations. Unit 6 Two-variable inequalities. Unit 7 Functions. Unit 8 Absolute value equations, functions, & inequalities.