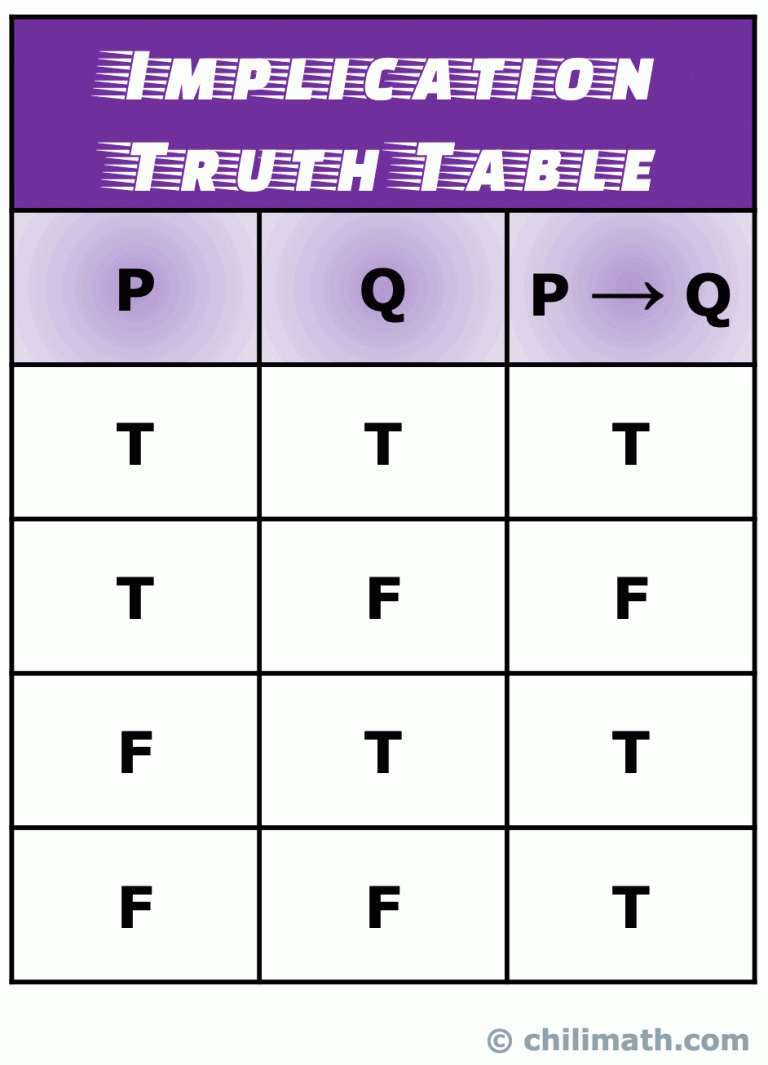
What this truth table represents is the fact that if you have a data set (or situations) that results in a false value of (~A V B) then your assumption that A implies B is violated (or is not correct). In simpler words, the true values in the truth table are for the statement A implies B. Truth Tables of Five Common Logical Connectives or Operators In this lesson, we are going to construct the truth tables of the five (5) common logical connectives or operators. They are considered common logical connectives because they are very popular, useful and always taught together.
Truth Tables of Five Common Logical Connectives or Operators ChiliMath
For each truth table below, we have two propositions: p and q. They can either both be true (first row), both be false (last row), or have one true and the other false (middle two rows). Writing this out is the first step of any truth table. The conditional - "p implies q" or "if p, then q" A biconditional is written as p ↔ q and is translated as " p if and only if q′′. Because a biconditional statement p ↔ q is equivalent to (p → q) ∧ (q → p), we may think of it as a conditional statement combined with its converse: if p, then q and if q, then p. The double-headed arrow shows that the conditional statement goes from. A truth table is a structured representation that presents all possible combinations of truth values for the input variables of a Boolean function and their corresponding output values. A function f from A to F is a special relation, a subset of A×F, which simply means that f can be listed as a list of input-output pairs. A truth table is a table whose columns are statements, and whose rows are possible scenarios. The table contains every possible scenario and the truth values that would occur. One of the simplest truth tables records the truth values for a statement and its negation. Figure %: The truth table for p, âàüp

Implication Truth Table Logical Connectives Stock Vector (Royalty Free
An implication is an "if-then" statement, where the if part is known as the antecedent, and the then pa. Learn how to create a truth table for an implication. Disjunction (OR) Negation Conditional or Implication Statements A Family of Seven Biconditional Logic Logic Gates Combining Arguments (in progress) See Also Conjunction (AND) Two simple statements can be converted by the word "and" to form a compound statement called the conjunction of the original statements. 1 The discussion is about why the statement ⊥ → ⊥ ⊥ → ⊥ is considered "true" rather than "false". That is, why the truth table of the conditional connective is defined as it is. An argument is considered valid if, it guarantees the conclusion is true when all the premises are true. Truth Table for Implication p q p → q F F T T F F T T The implication is only false if p is true and q isn't. It's true otherwise. The implication is only false if p is true and q isn't. It's true otherwise. You will need to commit this table to memory. We're going to be using it a lot over the rest of the week. You will need to.

Logical Implication Truth Table Explained Elcho Table
Truth Table for Implication p q p → q F F T T F F T T The implication is only false if p is true and q isn't. It's true otherwise. The implication is only false if p is true and q isn't. It's true otherwise. You will need to commit this table to memory. (Consider a tattoo on your forearm.) We're going to be using it a lot over the. A truth table is one of those things in mathematics that is much easier to understand when you see how it looks and how it works, than learning through its definition. Anyway, we will attempt to define it in order to have a baseline or basic understanding of what it is.. Implication or Conditional. Symbol: [latex]\Rightarrow[/latex] is read.
This tool generates truth tables for propositional logic formulas. You can enter logical operators in several different formats. For example, the propositional formula p ∧ q → ¬r could be written as p /\ q -> ~r , as p and q => not r, or as p && q -> !r . The connectives ⊤ and ⊥ can be entered as T and F . Solution. This is a complex statement made of two simpler conditions: "is a sectional", and "has a chaise". For simplicity, let's use S to designate "is a sectional", and C to designate "has a chaise". The condition S is true if the couch is a sectional. A truth table for this would look like this: S. C.
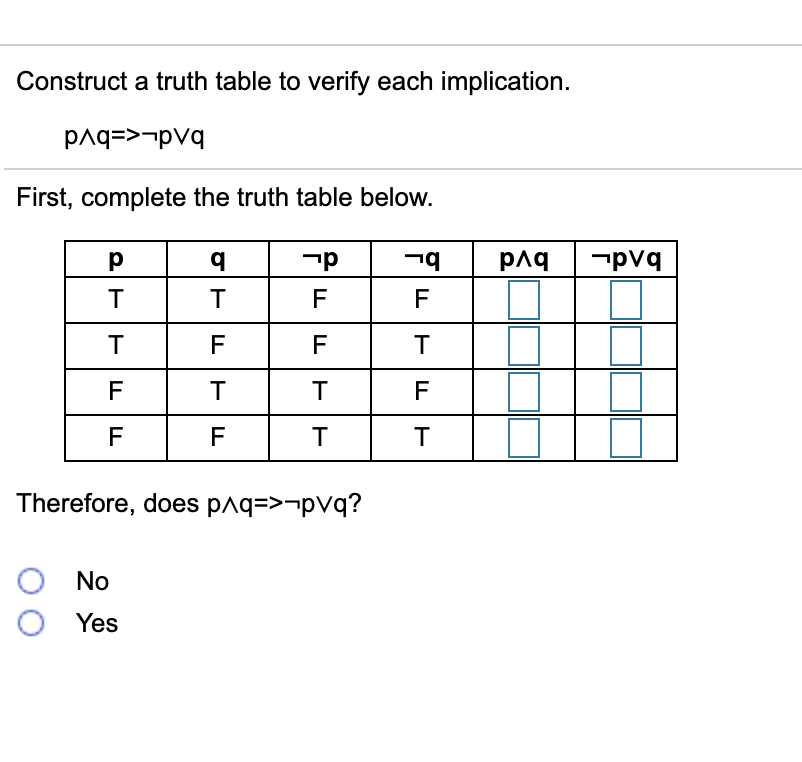
Solved Construct a truth table to verify each implication
Use a truth table to interpret complex statements or conditionals. Write truth tables given a logical implication, and its related statements. Determine whether two statements are logically equivalent. Because complex Boolean statements can get tricky to think about, we can create a truth table to break the complex statement into simple. Create a truth table for the statement A ⋀ ~(B ⋁ C) It helps to work from the inside out when creating truth tables, and create tables for intermediate operations. We start by listing all the possible truth value combinations for A, B, and C. Notice how the first column contains 4 Ts followed by 4 Fs, the second column contains 2 Ts, 2 Fs.




