Quadratische Funktionen haben eine quadrierte Variable (x²). Die einfachste (tschiraquade) Funktion hat die Gleichung y = x². Ihr Graph heißt (paraNormablle). Die Normalparabel verläuft symmetrisch zu der Achse, durch die das (Minumim) verläuft. Sie ist nach (bone) hin geöffnet. Übungsblatt mit Musterlösung zu Quadratische Funktionen, Parabeln; Quadratische Funktionen; Station 1 bis 5.
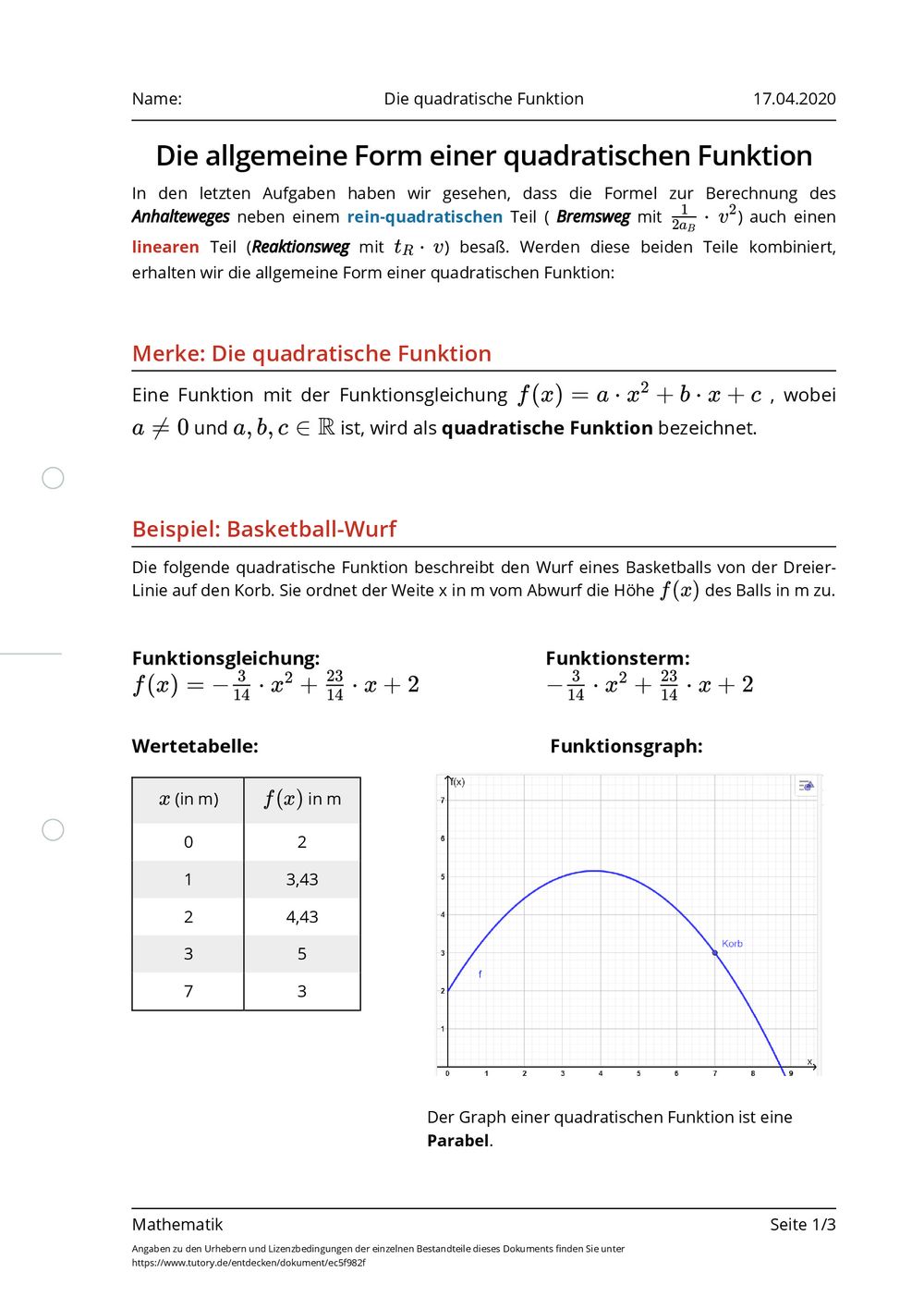
Arbeitsblatt Die quadratische Funktion Mathematik tutory.de
Aufgaben zu quadratischen Funktionen 1 Bestimme jeweils die Scheitelform der unten abgebildeten Parabeln. Lösung anzeigen 2 Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen. Der Graph der Funktion verläuft durch die Punkte A (1|1), B (3|4), C (5|-1) Lösung anzeigen Hier bist du richtig! Wir erklären dir alles, was du für Aufgaben zu diesem Thema beherrschen solltest: quadratische Funktionen zeichnen, Funktionsterme aufstellen, Nullstellen von quadratischen Funktionen berechnen und Anwendungsaufgaben lösen. Diese Aufgabentypen begegnen dir, sobald du es mit quadratischen Funktionen zu tun bekommst. Quadratische Funktionen - Mathe-Aufgaben und Online-Übungen | Mathegym Quadratische Funktionen - Matheaufgaben - Lehrplan für 8.-9. Jgst Aufgaben rechnen Stoff ansehen (+Video) Level 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Welche Funktionsgleichung beschreibt den Graph? y = x 2 + 3 y = x + 3 2 y 5 Wandle die Funktionsterme der in allgemeiner Form (Polynomform) gegebenen quadratischen Funktionen in die Scheitelpunktform um. a) f(x) = 2x2 − 16x + 35 d) f(x) = 5x2 + 10x + 9 b) f(x) = −0,5x2 + 2x − 1 e) f(x) = 5x2 + 3 c) f(x) = −2x2 − 12x + 21
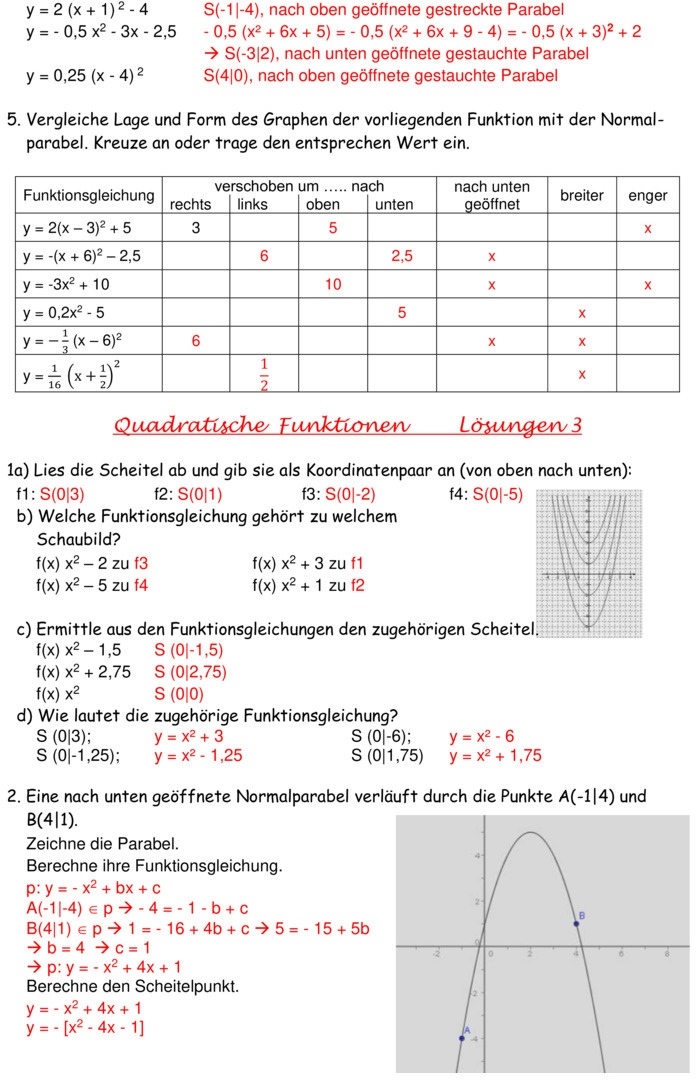
Übungsblatt zu Quadratische Funktionen
Hier findest du gemischte Aufgaben zum Thema quadratischen Funktionen. Schaffst du sie alle? 1 Welche Werte kann der Parameter t annehmen, so dass die folgenden Aussagen richtig sind? Der Graph der Funktion f mit f\left (x\right)=x^2+tx+1 f (x) = x2 + tx +1 verläuft vollständig oberhalb der x-Achse. Lösung anzeigen Online-Übungen zum Thema "quadratische Funktionen", die du direkt im Browser bearbeiten und lösen kannst. Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen. 33 Aufgaben, 7 Levels Quadratische Funktionen - Darstellungsformen Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen. Der Graph der Funktion verläuft durch die Punkte A (1|1), B (3|4), C (5|-1) Lösung anzeigen. Die Funktion besitzt eine doppelte Nullstelle bei x=3 und geht durch den Punkt P (2|0,3). Lösung anzeigen. Hier erklären wir dir alles, was du wissen musst! Inhaltsübersicht Quadratische Funktionen einfach erklärt zur Stelle im Video springen (00:18) Eine quadratische Funktion erkennst du daran, dass ein x2 vorkommt, aber kein x 3, x 4, x 5, usw… Der Graph einer quadratischen Funktion ist eine Parabel .

quadratische Funktionen.html
Einfach Mathe üben? Na, klar! Mit der Mathe Trainer App von Cornelsen Startseite > 9. Klasse > Quadratische Funktionen Quadratische Funktionen 12 Aufgaben: Zeichnen quadratischer Funktionen 8 Aufgaben: Zeichnen quadratischer Funktionen 12 Aufgaben: Bestimmung des Scheitelpunkts 12 Aufgaben: Bestimmung des Scheitelpunkts Jetzt gratis testen Quadratische Funktionen - Lösungen der Aufgaben a) Wie hoch ist die Brücke (von der Straße aus gemessen)? Die Höhe der Brücke von der Straße aus gemessen ist gesucht. Der höchste Punkt der Hängebrücke ist der Scheitelpunkt der Funktion. → S ist gesucht.
f ( x) = a x 2 + b x + c. heißt quadratische Funktion. Wegen y = f ( x) können wir statt f ( x) = a x 2 + b x + c auch y = a x 2 + b x + c schreiben. Charakteristische Eigenschaft. Im Funktionsterm quadratischer Funktionen kommt x in der 2. Potenz, aber keiner höheren Potenz vor. Bezeichnung. Aufgabensammlung, Funktionen, Ganzrationale Funktionen, Mathematik. Hier findest du Textaufgaben und Anwendungsaufgaben zu quadratischen Funktionen Teil I. 1. Eine Tordurchfahrt hat die Form einer Parabel. Sie ist 6 m hoch und 4 m breit. Ein Fahrzeug ist 3 m breit und 2,20 m hoch.

Quadratische Funktionen "Prototyp" und "Verwandte" Unterrichtsmaterial im Fach Mathematik
Quadratische Funktionen erkunden Cookies helfen uns bei der Bereitstellung von ZUM-Unterrichten. Durch die Nutzung von ZUM-Unterrichten erklärst du dich damit einverstanden, dass wir Cookies speichern. mit quadratischen Funktionen zu wiederholen und intensiv zu üben. Bevor du anfängst zu üben, solltest du eine spontane Selbsteinschätzung in Form einer Schulnote von 1 bis 6 abgeben. Anschließend kannst du die Testaufgaben bearbeiten und mit- hilfe der ausführlichen Musterlösungen auswerten. Nun kannst du gezielt üben. Selbsteinschätzung. II Quadratische Funktionen und Gleichungen 17.




