Binomische Formeln - Übersicht. Lesezeit: 1 min. Die drei binomischen Formeln muss man auswendig können, da man sie oft beim Rechnen benötigt. 1. Binomische Formel. ( a + b )· ( a + b) = a ² + 2· a · b + b ². 2. Binomische Formel. ( a − b )· ( a − b) = a ² − 2· a · b + b ². Als binomische Formeln werden üblicherweise die folgenden drei Umformungen mit dem Exponenten 2 bezeichnet: erste binomische Formel (Plus-Formel) zweite binomische Formel (Minus-Formel) dritte binomische Formel (Plus-Minus-Formel) Die Gültigkeit der Formeln ist durch Ausmultiplizieren einzusehen: Die binomischen Formeln hoch 3 lauten wie folgt:

Binomische Formeln MatheGuru
Folgende Inhalte werden angeboten: Eine Erklärung, was die Binomischen Formeln sind und wozu man diese braucht. Viele Beispiele zum Einsatz der Binomischen Formeln, vorwärts wie rückwärts. Aufgaben und Übungen mit denen ihr selbst üben könnt. Mit Musterlösungen für alle Übungsaufgaben. 1. Binomische Formel (Plus-Formel) $(a + b)^2 = a^2 + 2ab + b^2$ 2. Binomische Formel (Minus-Formel) $(a - b)^2 = a^2 - 2ab + b^2$ 3. Binomische Formel (Plus-Minus-Formel) $(a + b) \cdot (a - b) = a^2 - b^2$ Hier zeigen wir dir alle drei binomischen Formeln, jeweils erklärt mit vielen Beispielen. Du willst dich beim Lernen lieber zurücklehnen? Dann schau dir unser Video an! Inhaltsübersicht. Binomische Formeln einfach erklärt Erste binomische Formel Zweite binomische Formel Dritte binomische Formel Binomische Formeln hoch 3 Für alle, die Klammern ausmultiplizieren können, ist die erste binomische Formel eigentlich nichts neues, auch wenn sie auf den ersten Blick abschreckend wirkt. Denn diese lautet: 1. Binomische Formel: ( a + b )2 = a2 + 2ab + b2 Herleitung: ( a + b ) 2 = ( a + b ) · ( a + b ) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2

Binomische Formeln • einfach erklärt · [mit Video]
Es gibt drei binomische Formeln, die erste (Plus-Formel), die zweite (Minus-Formel) und die dritte (Plus-Minus-Formel) Alle drei kommen oft vor und sind wichtige Hilfsmittel zum Rechnen. 1. binomische Formel \displaystyle (a+b)^2=a^2+2ab+b_ { }^2 (a+ b)2 = a2 + 2ab +b2 Beispiel: Hier geben wir einen Überblick über die drei Formeln und zeigen, wie sie genutzt werden. In den kommenden Videos werden wir jede einzelne Formel genauer durchgehen. 1. Binomische Formel (a + b)² 2. Binomische Formel (a - b)² 3. Binomische Formel (a + b)* (a - b) Das Video erklärt euch alle drei Formeln und es zeigt euch zu jeder Formel Beispiele. Es gibt drei binomische Formeln. Diese sind ein wichtiges Hilfsmittel zur Vereinfachung von Termen und können in beiden Richtungen angewendet werden. Das bedeutet, dass sie sowohl zum Ausklammern, als auch zum Faktorisieren verwendet werden können. Was dich auf dieser Seite erwartet: Wie lauten die drei binomischen Formeln? Erste binomische Formel
Binomische Formeln Leicht erklärt, Übungen + Beispiele
Natürlich kann man die binomische Formel auch andersrum anwenden. Mit der binomischen Formel kann man zum Beispiel folgenden Ausdruck zusammenfassen: Wir müssen hierbei ein bisschen Aufpassen, da man nicht alle Terme dieser Art zusammenfassen kann. Wir müssen zunächst prüfen ob es sich tatsächlich um die erste binomische Formel handelt. Wir erklären dir was die binomischen Formeln sind, wo sie herkommen und wozu man die binomischen Formeln braucht
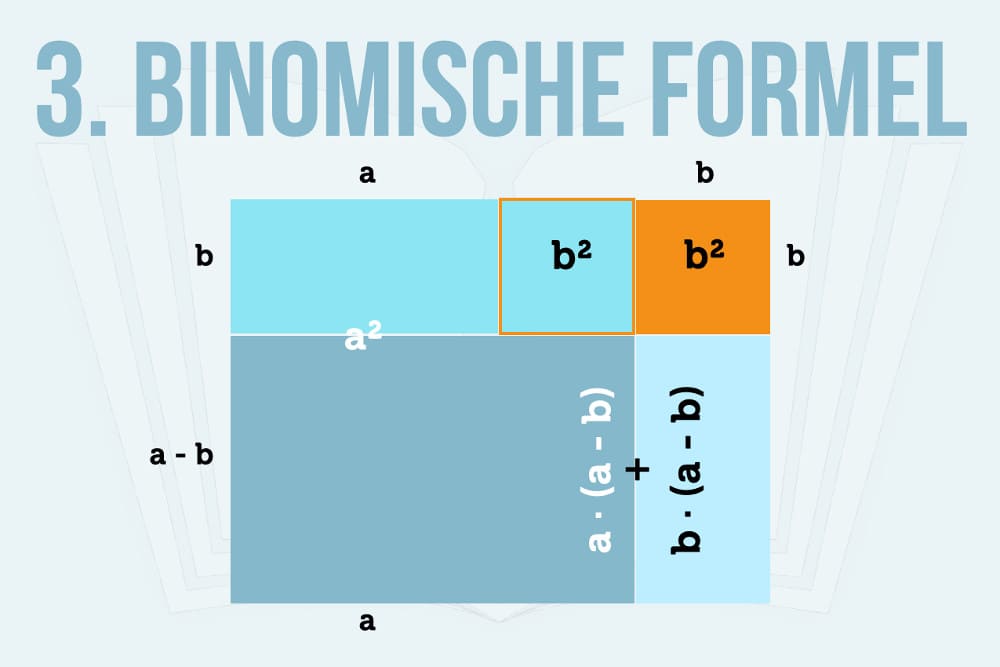
Es gibt drei binomische Formeln. Die drei binomischen Formeln lassen sich geometrisch herleiten. Binomische Formeln - Einführung Zunächst geben wir eine Übersicht über alle drei binomischen Formeln, bevor wir die Herleitung der binomischen Formeln erklären und uns Beispiele zum Rechnen mit den binomischen Formeln anschauen. Binomische Formeln helfen dir dabei, sogenannte Binome zu berechnen. Ein Binom ist ein Polynom mit zwei Gliedern. Da jedes Polynom wie folgt aufgebaut ist a 0 + a 1 x + a 2 x 2 +. + a n x n, n ≥ 0, kann man ein Binom als a n + b m schreiben.. Für bestimmte Binome kann man über die verschiedenen Rechengesetze Umformulierungen vornehmen, die das Rechnen erleichtern.

Binomische Formeln Leicht erklärt, Übungen + Beispiele
Binomische Formeln Übungen: Binomische Formeln Aufgaben mit Lösungen Erste, zweite und dritte binomische Formel Auflösen mit kostenlosem Video Alle binomischen Formeln ergeben sich aus den normalen Regeln zum Auflösen von Klammern in Gleichungen und sind somit nicht unbedingt notwendig, wenn man diese beherrscht. Allerdings erleichtern dir die binomischen Formeln das Rechnen und führen schneller zu einer Lösung. Was sind Binome?




