Energieerhaltungssatz Arbeitsblätter mit Übungen und Aufgaben zum Energieerhaltungssatz für Physik in der 8. Klasse am Gymnasium - mit Lösungen! Was bedeutet Energieerhaltung? Bei Energieumwandlungen sind verschiedene Energieformen beteiligt. Die Gesamtenergie eines geschlossenen Systems bleibt immer gleich. Physik * Jahrgangsstufe 9 * Aufgaben zum Energieerhaltungssatz 1. Die Kugel des abgebildeten Pendels wird ausgelenkt und dabei die Höhe h = 12cm angehoben. a) Mit welcher Geschwindigkeit schwingt die Kugel durch die Ruhelage? b) Wie hoch müsste man die Kugel aus- lenken, damit die Geschwindigkeit doppelt so groß wie bei Aufgabe a) ist? 2.

Energieerhaltungssatz einfach erklärt 1a Technikermathe.de
Energieerhaltungssatz Aufgaben mit Lösungen. Anbei eine Aufführung von verschiedenen Aufgaben zum Energieerhaltungssatz, die zum größten Teil auch Lösungen haben. Wir verlinken dabei auf die Aufgaben, sie sind kein Teil von www.physik-grundlagen.de ! Übungsaufgaben zur Energieerhaltung Vorbereitung - Lerne folgende Formeln auswendig! E 1 = mv2 kin 2 F = mg = G G E pot = mgh m2 1J =1Nm =1kg 1 E = Ds2 Spann 2 N s2 g = 9,81 kg Aufgaben 1. Rechne jeweils in die in Klammern angegebenen Einheiten um! % 1,8m a) km b) 63km h m s h s c) 15 cm m min h d) 1,7 g kg % 46Euro e) ct % mN N % cm3 m3 kg g Mathematisch kannst du die Energieerhaltung ausdrücken als E g e s = E k i n + E p o t + E s p a n n = k o n s t a n t. Dabei können sich die einzelnen Anteile der drei Energieformen fortlaufend ändern, wie z.B. bei einem Skater in der Halfpipe. Aufgaben Vorlesen Zwei Energieformen in der Halfpipe Energieformen 1 a 1 13: Energieerhaltung Ekin' = 2 Ekin ⇔ v'2 = 2v2 ⇒ v' = 2 v ≈ 113,1 km/h Aufgabe 14: Energieerhaltung a) Der Faden ist gerade nicht mehr gespannt, wenn die Zentripetalkraft Fz gerade gleich der Gewichtskraft Fg ist: Fz = Fg ⇔ mv 2 1 a 1 = mg ⇔ va = g r ≈ 2,83 m/s und Ekina = mva 2 = r∙m∙g = 0,4 J r 2 2
Energieerhaltungssatz Erklärung, Spezialfälle und Beispiel · [mit Video]
Zur Lösung verwendet man den Energiesatz (als Höhenbezugspunkt wählt man den tiefsten Punkt): Die Gesamtenergie in Punkt 1 (größte Auslenkung) ist gleich der Gesamtenergie im Punkt 2 (tiefster Punkt). Da in diesem Fall keine Spannenergie beteiligt ist, gilt somit \[E_{pot,1}+E_{kin,1}=E_{pot,2}+E_{kin,2}\] Energie und Energieerhaltungssatz In einem abgeschlossenen System bleibt bei Reibungsfreiheit die gesamte mechanische Energie erhalten. Verschiedenen Energieformen können lediglich ineinander umgewandelt werden (z.B. potentielle Energie, kinetische Energie, Spannenergie). Grundwissen Aufgaben Arbeit als Energietransfer Grundwissen Aufgaben Lösen Sie die folgenden Aufgaben nur mit Hilfe des Energieerhaltungssatzes. a) Mit welcher Geschwindigkeit v2 prallt die Masse m2 am Boden auf? Geben Sie v2 in Abhängigkeit von m1 , h und g = 9,81 m/s2 an. b) Bestimmen Sie v2 für h = 1,5m und m1 = 2,0 kg. c) Bestimmen Sie h so, dass v2 = 5,0 m/s gilt. y 0 a) Schnecke ( 35 g ) kriecht mit 12 cm min b) Schiff ( 145 t ) fährt mit 3,5 Knoten ( 1 Knoten = 1Seemeile) Stunde = 1,852 km h Aufgaben zum Energieerhaltungssatz: Lerne folgende Formeln auswendig lernen! W = F s E kin = E pot = mgh E spann = F G = mg 1 2 mv2 1 2 Ds 2 1 J = 1 Nm 1 J = 1 kg m g = 9,8 2 s2 N kg 3.
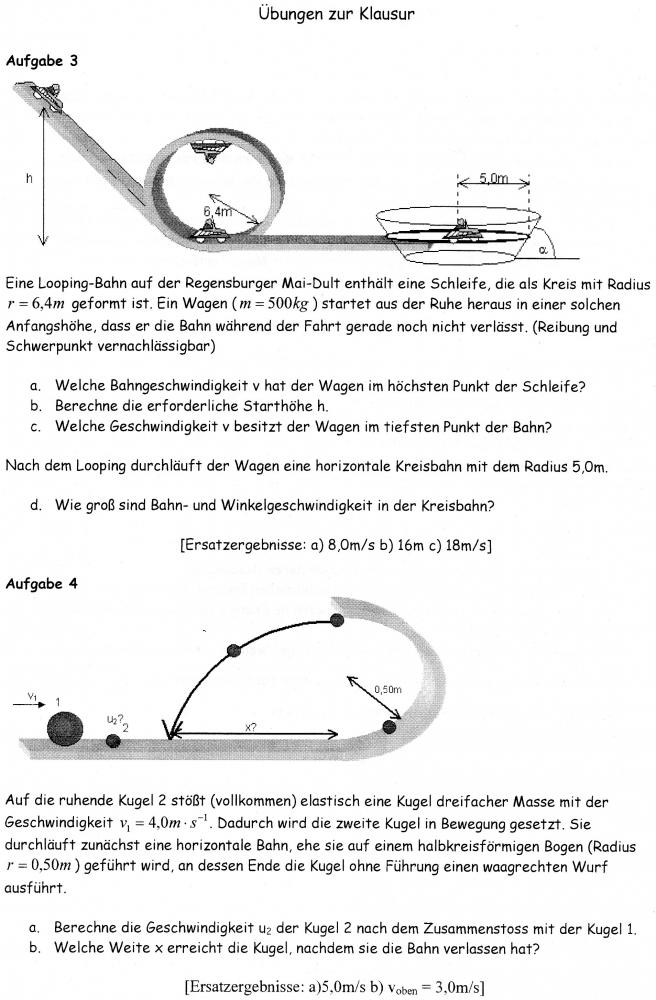
Übung zur Klausur Physik Looping aufgabe (klasse 11, Energieerhaltung, waagerechterwurf)
Energieerhaltung beim freien Fall. Schwierigkeitsgrad: leichte Aufgabe. Vorlesen. Abb. 1 Skizze zur Aufgabe. In Abb. 1 siehst du einen Körper der Masse m, der aus einer Höhe s losgelassen werden soll und dann frei (d.h. ohne Luftwiderstand) zu Boden fällt. Es sei m = 48 k g und s = 2, 0 m. Rechne mit g = 10 m s 2. a) Aufgabe 1: In diesem Abschnitt findet Ihr Rechenaufgaben und Fragen zur Energieerhaltung und Energieerhaltungsgesetz. Wer eine Frage oder Aufgabe nicht mag, der kann diese mit dem Button "Überspringen" übergehen. Zur ersten Frage: In welcher Einheit wird die Menge an Energie angegeben?
Aufgaben zur Energieerhaltung (Lösung) Aufgabe 1: Ein Ball (m = 0,2kg) wird mit der Anfangsgeschwindigkeit v0 = 10m/s nach oben geworfen. a) Welche Höhe erreicht er? Die Bewegungsenergie wird vollständig in Lageenergie umge-wandelt: 1⁄2 m v0 2 = mgh ↔ h=v02/(2g)=5,1m b) Welche Geschwindigkeit hat er in 1,8m Höhe? Der Energieerhaltungssatz besagt, dass in einem abgeschlossenen, reibungsfreien System die Summe aller Energien immer gleich bleibt. Bei der Energie handelt es sich also um eine Erhaltungsgröße. Ein abgeschlossenes System kannst du dir als einen Kasten vorstellen, der keine Energie hinein oder hinaus lässt.

Energieerhaltungssatz Zwei Aufgaben auf S.127 A2 und A5 YouTube
Der allgemeine Energieerhaltungssatz besagt, dass der Energieaustausch eines Systems mit seiner Umgebung gleich dem Energiefluss durch die Grenzflächen des Systems ist. Findet kein solcher Austausch statt, so gibt es auch keinen Energiefluss. Die Gesamtenergie des Systems ist also konstant. Nutze die Formel für Energieerhaltung: \[ W ~=~ W_{\text{kin}} ~+~ W_{\text{pot}} \] Gravitationsbeschleunigung beträgt: \( g ~=~ 9.8 \, \frac{\text m}{\text{s}^2} \) Lösung. Der Ball bekommt beim Hochwerfen eine Bewegungsenergie \(W_{\text{kin}}\). Ihr Wert ist abhängig von der Geschwindigkeit und der Masse des Balls.




