1 Bestimme den maximal möglichen Definitionsbereich folgender gebrochenrationaler Funktionen: f (x)=\frac {7x-3} {8x-5} f (x) = 8x−57x−3 Lösung anzeigen f (x)=\frac {x^3} {\left (x-1\right)^2}+7x f (x) = (x−1)2x3 +7x Lösung anzeigen f (x)=\frac1 {x (x-5)} f (x) = x(x−5)1 Lösung anzeigen 2 Teste dein Wissen! Hier findest du Aufgaben zur Kurvendiskussion gebrochen-rationaler Funktionen. 1 Führe bei den folgenden Funktionen eine Kurvendiskussion durch. (Definitionsbereich, Nullstellen, Verhalten an den Rändern des Definitionsbereichs, Asymptoten, Extrempunkte) Skizziere dann die Graphen.

Abitur Übungsaufgaben Gebrochen Rationale Funktionen
Funktionen, deren Funktionsterm ein Bruchterm ist, nennt man gebrochen rationale Funktionen. Bruchterme sind Terme, bei denen eine Variable im Nenner auftritt, wie zum Beispiel 1/x, 3/x+2, 2+z/z². In Bruchterme darf man nur solche Zahlen einsetzen, für die der Nenner nicht 0 wird, da man sonst durch 0 dividieren würde. Aufgaben zu einfachen gebrochen-rationalen Funktionen In diesem Aufgabenordner werden nur Funktionen der Form \displaystyle f (x)=\frac {a} {x+b}+c f (x) = x + ba +c ( a\in\mathbb {R}\setminus\ {0\} a ∈ R∖{0}, b\in\mathbb {R} b ∈ R, c\in \mathbb {R} c ∈ R) betrachtet. 1 Eine gebrochenrationale Funktion ist eine Funktion, bei der sich sowohl im Zähler als auch im Nenner eines Bruchs eine ganzrationale Funktion befindet. Zu den ganzrationalen Funktionen zählen u. a. lineare Funktionen und quadratische Funktionen. Beispiel 1 f ( x) = x 4 x − 1 Beispiel 2 Gebrochenrationale Funktionen haben die obige allgemeine Funktionsgleichung, aus der du bereits viele Eigenschaften ablesen kannst. Am wichtigsten ist dabei die Klassifizierung nach Zählergrad und Nennergrad. Der Zählergrad ist die höchste Potenz, die im Zähler vorkommt, als Nennergrad bezeichnet man die höchste Potenz des Nenners.
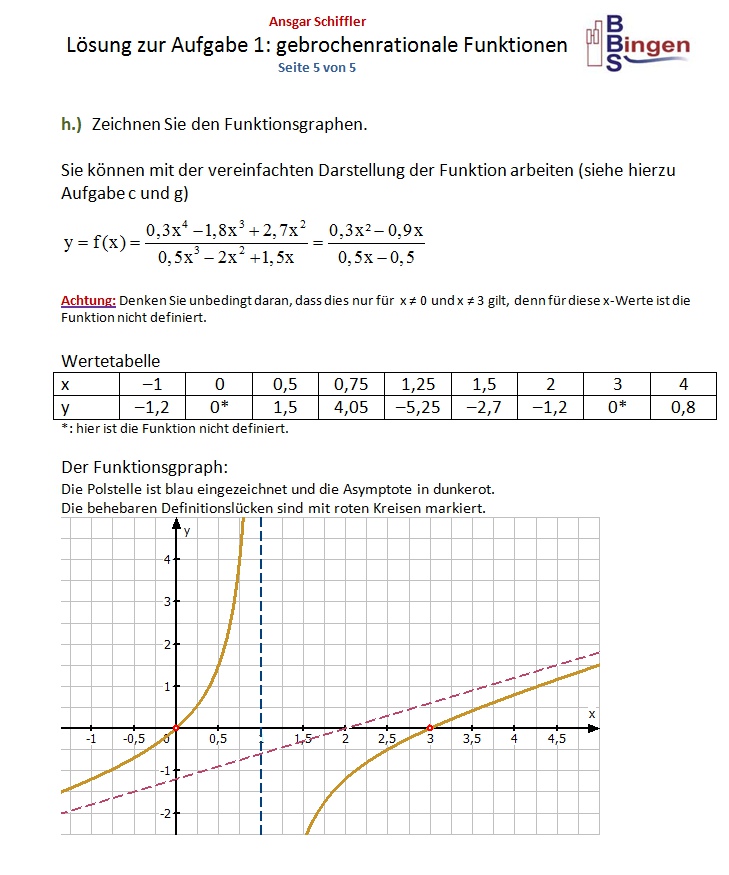
Gebrochenrationale Funktionen, Lösung zur Aufgabe 1
Teste dein Wissen zu gebrochen-rationalen Funktionen mit diesen Anwendungsaufgaben! 1 Anwendungsbeispiele: Zur Bestimmung der Schwerkraft y (in N) auf einen Körper der Masse 1kg in der Entfernung x von der Erdoberfläche (in km) gilt die Formel y=\frac {4\cdot10^8} {\left (6370+x\right)^2} y = (6370+x)24⋅108 . Was erhält man für x=0? Gebrochenrationale Funktionen einfach erklärt Viele Mathematik-Themen Üben für Gebrochenrationale Funktionen mit interaktiven Aufgaben, Übungen & Lösungen. 01 Elementare gebrochen-rationale Funktionen. 4 Aufgabe 1: Gegeben sind im Folgenden die auf ihrem maximalen Definitionsbereich gegebe-. Klicke hier oder verwende den QR-Code, um die Aufgaben 1 und 2 zu überprüfen. 02 Wertemenge einer Funktion bestimmen: Übungen : 8 : gebrochen-rationale Funktionen › Mathe-Aufgaben Online-Übungen zum Thema "gebrochen-rationale Funktionen", die du direkt im Browser bearbeiten und lösen kannst. Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen. 51 Aufgaben, 10 Levels Elementare gebrochen-rationale Funktionen

Gebrochen rationale Funktionen Übungen und Aufgaben mit Lösungen
Gebrochen rationale Funktion Zählergrad < Nennergrad Wendepunkte und das Krümmungsverhalten Im Wendepunkt und im Flachpunkt ist das Krümmungsver-halten gleich Null. Erklärung Was ist eine gebrochenrationale Funktion? Die Standardform einer gebrochenrationalen Funktion ist gegeben durch: Dabei sind und ganzrationale Funktionen. Eine Stelle ist Nullstelle der Funktion , falls und gleichzeitig gilt. Ist , so ist eine Definitionslücke von . Gilt und , so ist die Definitionslücke eine Polstelle von .
Gebrochen-rationale Funktionen - Matheaufgaben. Definitionslücken und Verhalten der Funktion in deren Umgebung, Erkennen waagrechter und senkrechter Asymptoten, Grafen ohne Wertetabelle skizzieren - Lehrplan G8 (12. Klasse) Aufgaben rechnen. Stoff ansehen. Q11 * Mathematik * Gebrochen rationale Funktionen * Aufgaben 1. Geben Sie den maximal möglichen Definitionsbereich an und untersuchen Sie das Verhalten des Graphen an den Definitionslücken sowie für x o r f. Skizzieren Sie den Graphen und prüfen Sie Ihre Skizze mit Hilfe eines Funktionsplotters. a) 2 2x f(x) 0,2x 1 b) 2 0,5x 2 g(x) 1x c) 2 2x

Gebrochenrationale Funktionen Level 1 Grundlagen Blatt 2
1,994. f (x) Lösung anzeigen. Mathe-Aufgaben online lösen - Gebrochen-rationale Funktionen / Bestimmung und Klassifizierung von Polstellen; Erkennen behebbarer Definitionslücken, senkrechter, waagrechter und schräger Asymptoten; Zeichnung des Graphen; Ermittlung gebrochen-rationaler Funktionen aufgrund vorgegebener Eigenschaften. Gebrochen rationale Funktionen1 Übungsaufgaben zu gebrochen rationalen Funktionen Bestimme den maximalen Definitionsbereich und bilde die erste Ableitung: 1 1 + x f(x) = b) f(x) = 4x3 + c) f(x) = 2 x x 1 − x 1 − x d) f(x) = 1 + x g) f(x) = 2 x − a ; a∈ 3 x 2 x − 2 j) f(x) = 2 x + 4 2x − 4 e) f(x) = 1 − x h) f(x) = 1 (x + 1) 2




