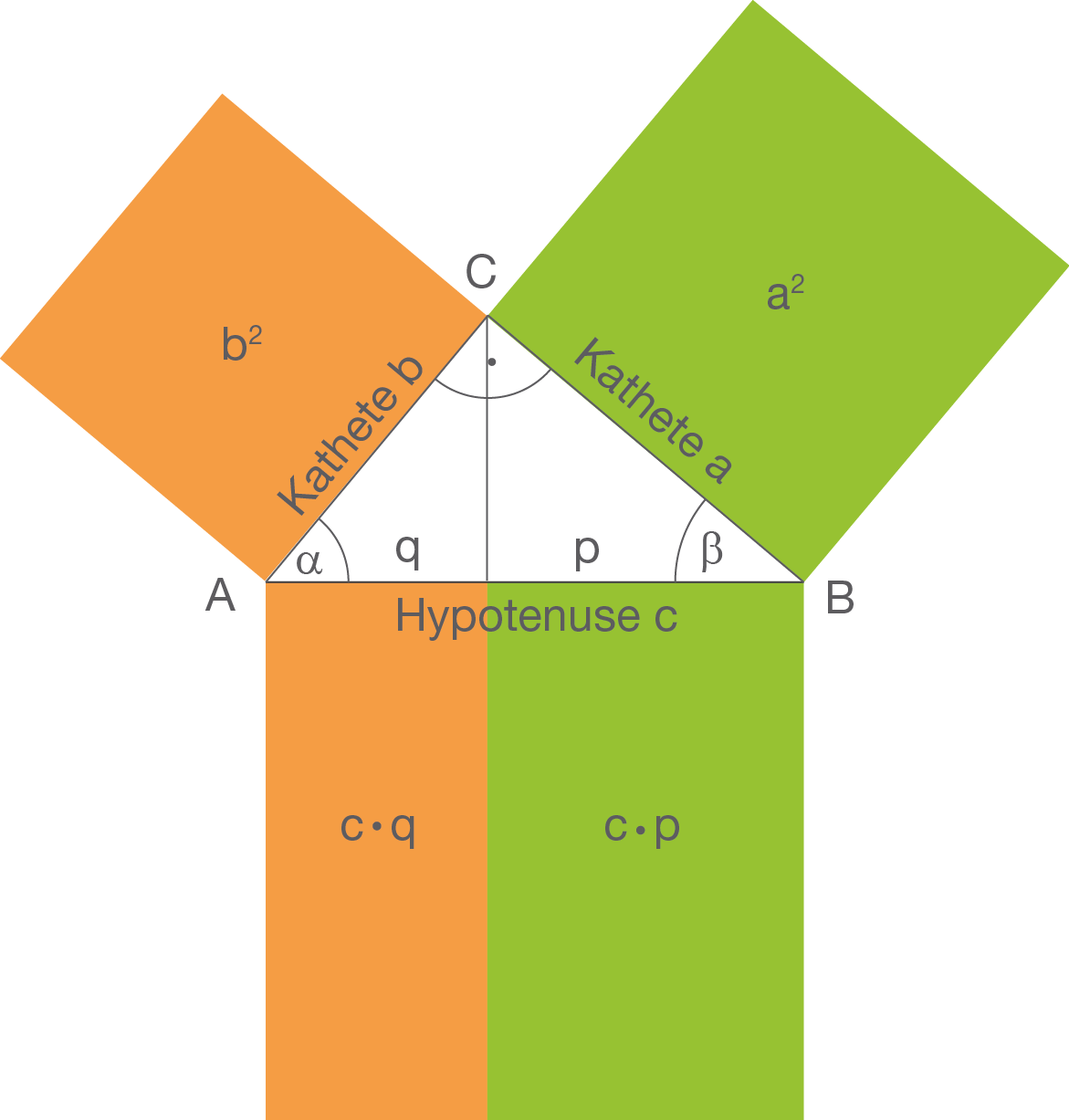
Durch die Höhe h h h wird die Hypotenuse in die Abschnitte p p p und q q q geteilt. Der. Höhen- und Kathetensatz. a und b sind die Katheten des Dreiecks. c ist die Hypotenuse und besteht aus zwei Abschnitten . h ist die Höhe im rechtwinkligen Dreieck. Der Höhensatz des Euklid macht dann eine Aussage über die Höhe h im Dreieck. Der Kathetensatz des Euklid kann auf beide Katheten angewendet werden.

Höhensatz und Kathetensatz Learnattack
Kathetensatz und Höhensatz Kathetensatz (A 1 - A 7) Höhensatz (A 8 - A 14) Kathetensatz Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete genauso groß wie das Rechteck aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt, der durch die Höhe markiert ist. Die neuen beiden Sätze, die du jetzt lernst, sind der Höhensatz und der Kathetensatz. Es ist egal, wo die Hypotenuse liegt. Jede Höhe auf einer Hypotenuse teilt das Dreieck in 2 weitere rechtwinklige Dreiecke. Erklärung der Konstruktion: Zeichne die Normale zum Eckpunkt C ein (das ist auch die Höhe h). Die Seitenlänge c wird somit in zwei Teile geteilt, die wir p und q nennen. Es gilt, dass h2 = p ⋅ q . Veranschaulichung des Kathetensatzes: 0,0 Kathetensatz: p q c a b Höhensatz & Kathetensatz des Euklid einfach erklärt - Erklärung, Beispiel, Anwendung. Dieser Satz ist nur bei rechtwinkligen Dreiecken anwendbar. Dabei teilt die Höhe h die Hypotenuse c in.
Kathetensatz Geometrie in der Ebene Mathe Digitales Schulbuch Skripte SchulLV.de
Es gelten der Höhen- und der Kathetensatz: Höhe 2 = Produkt der Hypotenusenabschnitte Kathete 2 = Hypotenuse · anliegender Abschnitt Beispiel 1 Bestimme in den skizzierten Dreiecken jeweils x. Lösung anzeigen (+Video) Beispiel 2 Konstruiere 24 mit Hilfe des Höhensatzes mit Hilfe des Kathetensatzes mit Hilfe des Satzes von Pythagoras Höhensatz und Kathetensatz In einem rechtwinkligen Dreieck teilt die Höhe die Hypotenuse c in 2 Abschnitte. Diese 2 Abschnitte (p und q) werden als Hypotenusenabschnitte bezeichnet. Hier erfahrt ihr alles zum Höhensatz und Kathetensatz, mit welchen ihr in rechtwinkligen Dreiecken rechnen könnt. Höhensatz Der Höhensatz besagt, dass das Quadrat der Höhe dasselbe ist, wie die beiden Teile der Hypotenuse, welche durch die Höhe geteilt werde, miteinander multipliziert. Alle akzeptieren und schließen Höhensatz und Kathetensatz leicht und verständlich erklärt inkl. Übungen und Klassenarbeiten. Nie wieder schlechte Noten!
Höhen und Kathetensatz? (Geometrie, Trigonometrie, Dreieck)
Dreieck Dreiecksarten Rechtwinkliges Dreieck Kathetensatz Kathetensatz In diesem Kapitel besprechen wir den Kathetensatz. Inhaltsverzeichnis Wiederholung: Rechtwinkliges Dreieck Der Satz Veranschaulichung Anwendungen Katheten gesucht Handelt es sich um ein rechtwinkliges Dreieck? Erforderliches Vorwissen Rechtwinkliges Dreieck Was ist der Kathetensatz des Euklid? Was sagt er aus? Wofür braucht man das? Was macht man damit? Ich erkläre es Dir!Moin,ich hoffe, dass Dir dieses Video ge.
Jede Basisgruppe besteht aus zwei Kathetensatz-Experten und einem Höhensatz-Experten. Gemeinsam hat jede Basisgruppe den Höhensatz sowie die beiden Bestandteile des Kathetensatzes gefunden. Die beiden Kathetensatz-Experten vergleichen und ergänzen zunächst ihre Ergebnisse und erklären sie dann dem Höhensatz-Experten. In diesem Video geht es um den Kathetensatz und Höhensatz von Euklid. Dies erkläre ich an jeweils einem Beispiel. Bevor ihr euch dieses Video anschaut, sollt.

Voraussetzungen Satz des Pythagoras, Höhenund Kathetensatz.Aufgaben und Anwendungen auf drei
Der Kathetensatz sagt dir, dass das Quadrat einer Kathete gleich dem Produkt des zugehörigen Hypotenusenabschnitts und der Hypotenuse ist. Kathetensatz Beispiel zur Stelle im Video springen (01:02) Schau dir gleich an, wie du den Kathetensatz (auch: Kathetensatz des Euklid) anwenden kannst. Was kann man mit a, b, c und h c berechnen ? Es kann der Flächeninhalt A des Dreiecks bestimmt werden. A = a · b /2 ; A = h c · c/2 → a · b/2 = h c · c/2 → h c = (a · b )/ c Die Höhe teilt die Hypotenuse in zwei Abschnitte p und q. Wie lang ist q ? Abb. 2 . q 2 + h c 2 = b 2 → q 2 = b 2 - h c 2




