Aufgaben zur Lagebeziehung von Geraden und Ebenen Lerne mit diesen Übungsaufgaben die Lagebeziehung von Geraden und Ebenen zu untersuchen. Schaffst du sie alle? 1 Bestimme jeweils die Schnittmenge von Ebene und Gerade. {\mathrm E}_1:\; {\mathrm x}_1+ {\mathrm x}_2-2\cdot {\mathrm x}_3=-3 E1 : x1 + x2 − 2⋅ x3 = −3 und Lagebeziehung Gerade Ebene: Aufgaben | StudySmarter Mathe Geometrie Lagebeziehung Gerade Ebene Lagebeziehung Gerade Ebene Algebra 2x2 Matrix Determinante Addition Additionstheoreme Additionsverfahren Antiproportionale Zuordnung Arten von Gleichungen Assoziativgesetz Ausklammern und Ausmultiplizieren Besondere Matrizen Betrag und Gegenzahl
Lagebeziehung Von Geraden Aufgaben Lagebeziehung Gerade Gerade Aufgaben Mit Lösungen Pdf
Lagebeziehungen von Geraden und Ebenen gehören zu dem übergeordneten Thema der Vektorrechnung und wird dir früher oder später in der Schule begegnen. Wir haben für dich alle Informationen rund um das Thema Lagebeziehungen in leicht verständlicher Sprache aufbereitet und mit Lernvideos ergänzt. Inhaltsverzeichnis Grundlagen Lagebeziehungen Lösungen - Abstand Punkt / Ebene. Aufgaben-Abstand_Punkt_Ebene-Lösungen.pd. Adobe Acrobat Dokument 48.6 KB. Download. Hier findet man erklärende Texte und Aufgaben mit Lösungen zum Thema Geraden und Ebenen in der Analytischen Geometrie. Liegen die Gleichung beider Ebenen E und F in der Parameterform vor, ermittelt man zunächst mithilfe des Vektorprodukts der Richtungsvektoren einer Ebenengleichung mindestens einen Normalenvektor n → E bzw. n → F (vgl. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform ). Untersuchung der Lagebeziehung zweier Ebenen Hier findest du Aufgaben zur Lagebeziehung zweier Ebenen. Lerne, die Lagebeziehung zu untersuchen und lineare Gleichungssysteme zu lösen! 1 Untersuche die gegenseitige Lage der gegebenen Ebenen in Koordinatenform. Bestimme die Schnittgerade, falls sich die Ebenen schneiden. {\mathrm E}_1:\;- {\mathrm x}_1+2\cdot {\mathrm x}_2+ {\mathrm x}_3=1 E1

Gegenseitige Lage von Geraden GeoGebra
Aufgaben zur Lagebeziehung zweier Geraden Lerne mit diesen Aufgaben die Lagebeziehungen von Geraden zu untersuchen. Schaffst du sie alle? 1 Bestimme die Lage der Geraden zueinander und berechne ihren Schnittpunkt wenn er exisitiert. Ebenen (02.04.2020) H. Wuschke Aufgabe 1 (8 BE) 0 5 1 0 2 1 Eine Gerade g ist gegeben durch g : #x = @ 3 A + t @ 1 A ; t 2 R 1 4 a) Geben Sie eine zweite zu g identische Gerade h an. 0 3 1 0 4 1 z.B. h : #x = @ 4 A + s @ 2 A ; s 2 R 3 8 b) Geben Sie Lagebeziehung Ebene-Ebene. In diesem Abschnitt lernst du, wie du die Lagebeziehung zwischen einer Gerade und einer Ebene in Koordinatenform bestimmen kannst. Wenn die Ebene in Parameterdarstellung vorliegt, kannst du sie - wie im Abschnitt Umwandlung Parameterform zu Koordinatenform beschrieben - in Koordinatenform umwandléln. Abituraufgaben zum Thema: Lagebeziehung Gerade und Ebene In vielen Abituraufgaben im Fach Mathematik wiederholen sich häufig die Themen und Aufgabenstellungen. Mit Hilfe dieser Zusammenstellung kannst Du dich Thema für Thema auf die Abiturprüfung vorbereiten. Eine Übersicht der Themenbereiche findet man unter Übersicht Themen in Abituraufgaben

Lage von Gerade zu Ebene Gymnasium Geraden und Ebenen StrandMathe Übung 1 YouTube
2.3.4 Lotgeraden und orthogonale Ebenen. Kategorie: 2.3 Lagebeziehungen von Geraden und Ebenen. Skalarprodukt. Normalenvektor. Ebenengleichung in Normalenform. Vektorprodukt. Extremwertaufgabe. Orthogonalität zweier Vektoren. Schnittpunkt einer Gerade mit einer Ebene. Abiturskript - 2.2.4 Umwandlung: Parameterform - Normalenform ). Untersuchung der Lagebeziehung zwischen Gerade und Ebene. Man überprüft zuerst die Gültigkeit der Gleichung u → ∘ n → E = 0. Gilt u → ∘ n → E = 0 sind der Richtungsvektor u → der Gerade g und der Normalenvektor n → E der Ebene E zueinander senkrecht.
Einleitung. Lagebeziehungen zwischen zwei geometrischen Objekten im dreidimensionalen Raum machen eine Aussage darüber, wie diese im Raum zueinander liegen. Es sind zu unterscheiden. Lagebeziehung Punkt-Gerade. Lagebeziehung Punkt-Ebene. Lagebeziehung Gerade-Gerade. Lagebeziehung Gerade-Ebene. Löse dann die Aufgaben. Kontrolliere anschließend die Ergebnisse. Notiere zum Schluss die Anzahl der richtigen Aufgaben. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnitt-punkt. : r æ ç = ç ç è ö ÷ 0 ÷ + 0 ÷ ø æ - 1 ö ç ÷ r × ç- 4 ÷ ç è 7 ÷ ø ; E : 2) æ ç :x = ç ç è 2 ÷ ö ç æ 1 r × ç- 1 ç è 1 ö ÷ 2 ÷ +
Mathematik 12/Lagebeziehung EbeneGerade RMGWiki
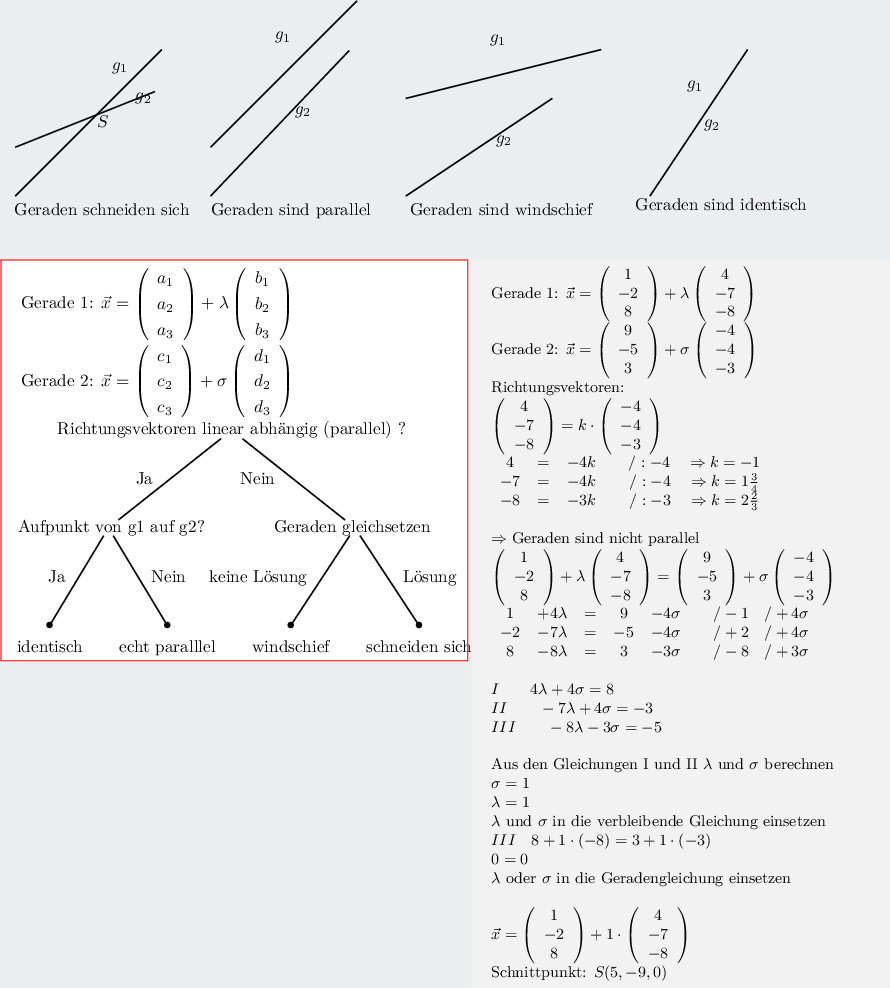
Genaue Lagebeziehung bestimmen: 2.1. Punkt einsetzen: Sind die Richtungsvektoren linear abhängig, dann sind die Geraden g und h entweder identisch oder parallel. Um das herauszufinden, setzt du einen Punkt der Gerade g in die Gerade h ein. → Liegt der Punkt auf der Gerade h, dann sind die Geraden identisch. 17 Ebenen Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0. → Was bedeutet das? Bestimme die Lage der Geraden zueinander und berechne ihren Schnittpunkt wenn er exisitiert.Weitere Aufgaben zu diesem Thema




