0:00 / 6:45 Gleichungssystem lösen mit Parameter, Gauß-Algorithmus | Mathe by Daniel Jung Mathe by Daniel Jung 914K subscribers Subscribe Subscribed 1.6K 260K views 9 years ago. Lineare Gleichungssysteme mit Parametern Ein Beispiel eines linearen Gleichungssystems mit Parameter ist das folgende: 3x1 2x2 + x3 = 2r 5x1 4x2 x3 x1 + 3x2 2x3 = 2 = 2r + 6 Benutzt man zur Losung die Methode des Kreuzprodukts, so schreibt man zuerst das LGS in Vektorform: 3 x1 5 + x2 1 4 + x3 1 = 3 2 2r 2 : 2r+6

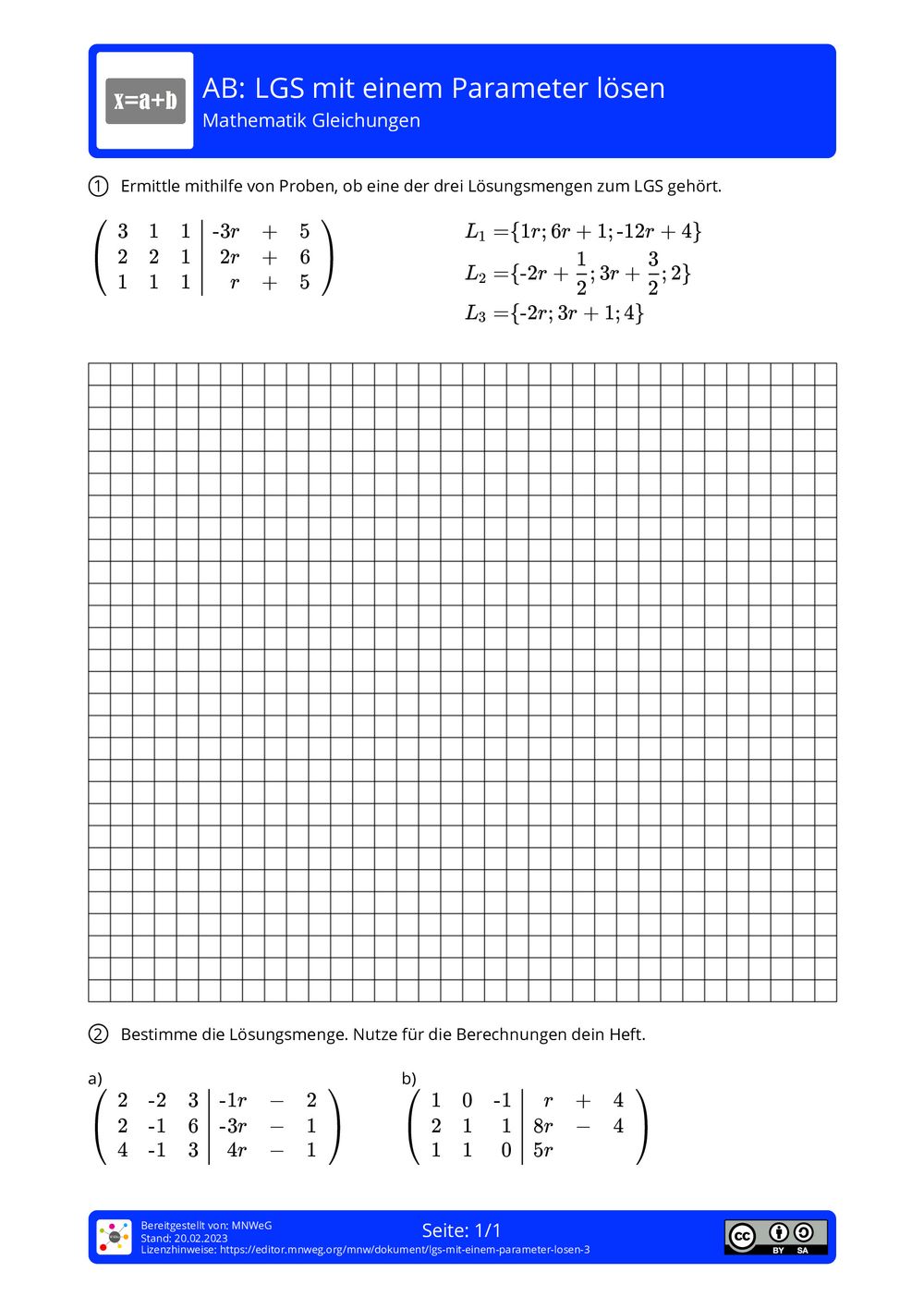
Arbeitsblatt LGS mit einem Parameter lösen Mathematik Gleichungen
Gauß Algorithmus mit Parameter In diesem Mathe Lernvideo erkläre ich (Susanne) wie man ein Gleichungssystem mit Parametern lösen kann. Wir schreiben das LGS in die Matrixschreibweise um. Auch mit Parametern gelten alle dir bekannten Regeln zum Lösen von Gleichungen. Erinnere dich zum Beispiel an das Waagemodell um die Gleichung zu lösen. Bei Parametergleichungen bringst du alle Elemente mit x auf die eine Seite der Gleichung. Beispiel: x + a = 2a - 3x ∣ - x a = 2a - 4x ∣ - 2a - a = - 4x ∣: ( - 4) a 4 = x Um die Lösbarkeit von Linearen Gleichungssystemen (LGS) zu bestimmen, gibt es mehrere Möglichkeiten. Eine Methode, die immer funktioniert, ist der Gauß Algor. Aufgaben: Aufgabe 20: Lösbarkeit eines linearen Gleichungssystems mit Parameter (3x3) Aufgabe 552: Lösungsmenge eines linearen Gleichungssystems mit Parameter (3x4) Aufgabe 753: Diskrete Fourier-Transformation eines tridiagonalen, zyklischen Gleichungssystems. Aufgabe 1516: Fehlerverhältnis bei linearen Gleichungssystemen.
Arbeitsblatt LGS mit einem Parameter lösen Mathematik Gleichungen
Dies ist das dritte Übungsvideo zum Lösen von Linearen Gleichungssystemen (LGS) mit Parameter. Bei dieser Aufgabe kommt der Parameter auf der Ergebnisseite vor, ist aber auch Bestandteil des. Solves a linear equation system with 2 equations and 2 variables. Send feedback | Visit Wolfram|Alpha Get the free "Gleichungssystem mit 2 Unbekannten" widget for your website, blog, Wordpress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha. In diesem Übungsvideo geht es um das Lösen eines Linearen Gleichungssystems (LGS), das neben den Variablen auf der Ergebnisseite auch einen Parameter r enthä. einem 3x3 LGS" im Unterrichtsgang evtl. nützlich sein. Weitere Anwendungen der linearen Gleichungssysteme finden sich im Basisfach bei der Berech-nung des Schnittpunkts zweier Geraden und eventuell beim Schnitt Gerade - Ebene in Parameter-form, die Schnittgebilde von Ebenen werden nicht berechnet. Darüber hinaus spielen lineare Glei-

GaußAlgorithmus III LGS mit PARAMETER lösen YouTube
IQB Pool: LGS mit Parameter links | Mathematik vom Mathe Schmid Schmid happens 353 subscribers Subscribe 36 views 8 months ago IQB Pool: LGS mit Parameter links Aufgabe 970 LGS IQB aus Hurra. Einleitung. Ein lineares Gleichungssystem (kurz LGS) ist in der linearen Algebra eine Menge linearer Gleichungen mit einer oder mehreren Unbekannten. Eine Lösung eines LGS muss alle Gleichungen gleichzeitig erfüllen. In diesem Abschnitt werden LGS mit drei Gleichungen und drei Unbekannten behandelt, und du lernst hier, wie du es lösen kannst.
Dies ist das zweite Übungsvideo zum Lösen eines Linearen Gleichungssystems (LGS) mit Parameter. Hier wird sich ergeben, dass vom Parameter abhängt, ob das LG. LGS mit Parameteren zu diskutieren, den Rang eines LGS bestimmen und die Lösungen konkret nach dem Satz von Rouché-Capelli zu klassifizieren, LGS auf beliebigen Körpern ( \ (\mathbb {R}\), \ (\mathbb {Q}\), \ (\mathbb {C}\), \ (\mathbb {Z}_2\), \ (\mathbb {Z}_3\), ⋯) zu lösen,

Gleichungssystem lösen mit Parameter, GaußAlgorithmus Mathe by Daniel Jung YouTube
Übungen zu LGS mit Parameter Bestimmen Sie den Wert des Parameters a so, dass das LGS keine eindeutige Lösung hat. 1 x x 2 x 2 ax x 2 x 3 2 x 2 3 2 3 x 1 b. 2 x x 1 2 x 2 x ax 3 x 2 x 3 2 2 1 2. Bestimmen Sie die Lösungen der folgenden LGS in Abhängigkeit von a; führen Sie dabei eine Fallunterscheidung durch. ax 1 4 x Diese Seite soll Ihnen helfen ein lineares Gleichungssystem auf seine Kompatibilität zu analysieren (durch Anwendung des Rouché-Capelli theorem ), die Anzahl der Lösungen zu bestimmen, ein lineares Gleichungssystem (LGS) mit dem Gauß-Verfahren, mithilfe der Kehrmatrix oder dem Cramer-Verfahren zu lösen, sowie die Gesamtlösung, partikuläre Lösung.




