Kurze Videos erklären dir schnell & einfach das ganze Thema. Jetzt kostenlos ausprobieren! Immer perfekt vorbereitet - dank Lernvideos, Übungen, Arbeitsblättern & Lehrer-Chat. Unsere Arbeitshefte eignen sich perfekt für Vertiefungen der Lerninhalte. Sie motivieren zum Lernen, machen Mut und schaffen Vertrauen in die eigenen Fähigkeiten.
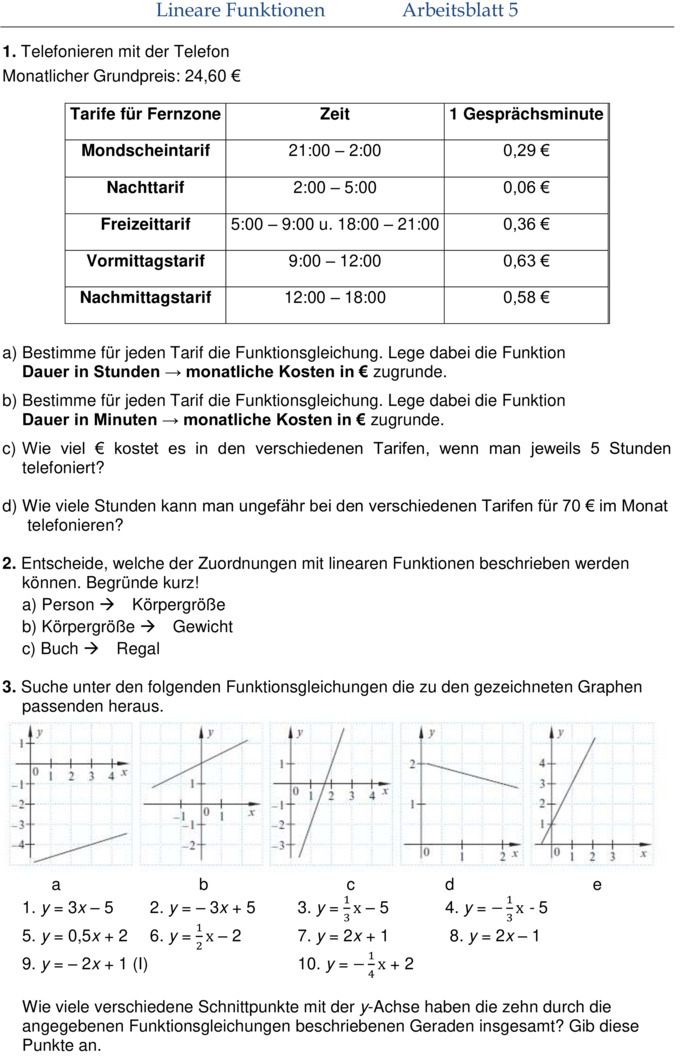
Lineare Funktionen Aufgaben Pdf
Dies ist Teil 3 der Übungsreihe "Lineare Funktionen". Inhalte: * Bestimmen von Funktionsgleichungen linearer Funktionen bei gegebenem Steigungsfaktor und y-Abschnitt * Abstand zweier Punkte * Parallele Geraden * Umformen von Funktionsgleichungen in die Normalform. Vorschau | Download PDF | Download Lösung. Aufgabe 1: Ablesen von linearen Funktionen Welche (linearen) Funktionen gehören zu den folgenden Funktionsgraphen? Aufgabe 2: Zeichnen von linearen Funktionen Zeichnen Sie die folgenden linearen Funktionen in ein Koordinatensystem : 3 1( ) = 4 1( ) = + 1 h1( ) = − + 3 2( ) = −2 2( ) = 5 − 4 4 h2( ) = − 5 − 1,5 3( ) = 0,5 2 Bemerkung: Die 378 Arbeitsblätter zum Thema "Lineare Funktionen" bieten 1512 Aufgaben in denen Graphen gezeichnet oder Funktionsgleichung ermittelt werden müssen. Dabei dienen Wertetabellen (inklusive Brüchen und Dezimalzahlen), Steigungsdreiecke oder auch vorgegebene Punkte als Lösungsansatz. Eine lineare Funktion ist eine Funktion f mit f (x) = m · x + b. Ihr Graph ist eine Gerade mit der Gleichung y = m · x + b. Dabei ist m die Steigung, b der y-Achsenabschnitt. Für den Steigungswinkel α der Geraden gilt: m = tan (α). Beispiel: f (x) = _ 2 x + _ 3 2 ist eine lineare Funktion.

Mathe (Lineare Funktionen) PDF
1. Gegeben sind die beiden Funktionen. (b) Zeichne die Graphen der beiden Funktionen in das Koordinatensystem. aus dem Graphen ablesen kann. Achsenabschnitts. (e) Erläre die Bedeutung der Steigung. 2.Wir sehen die Graphen von f (x) = x +1, g(x) = 1 3x, h(x) = 1 3x +3, i(x) = 4x 4 und j(x) = 4. 2 Bestimme die Funktionsgleichungen der abgebildeten linearen Funktionen. 3 Bestimme eine lineare Funktion, deren Graph durch die vorgegebenen Punkte verläuft. a) (1 |3), (3 |7) b) (0 |1), (5 |0) c) (−3 |1), (4 |−2) d) (−7 |−4), (−3 |−5) e) (0,5 |0,3), (1,3 |0,9) f) (4 |2), (−3 |2) g) (320 |16), (650 |24) h) 5 3 | 2 5, 3 4 | 5 2. Lineare Funktionen: Übungsblätter für die Klassenarbeit Funktionsgleichung bestimmen o Ein Punkt und die Steigung m sind bekannt o Ein Punkt und der Achsenabschnitt b sind bekannt o Zwei Punkte sind bekannt 9. Aufgabe Bestimmen Sie die Gleichung der Geraden [f(x) = mx + b]. 1 ; b) y 1 ( x 1) 2 c) 2 x 5 y 1 0 2 2 4 8. Bestimme die Gleichung der zu g orthogonalen Geraden g', die durch den Punkt P verläuft mit Hilfe der Punkt-Steigungsform a) g: y = -2x + 1; P(5|2) b) g: y = 0,25x - 1; P(0|2) g : y = -x - 3 ; P(1|5)

Lineare Funktionen Aufgaben Mit Lösungen Klasse 10 / Aufgaben Ableitungsfunktion und ihre
Aufgaben zu Lineare Funktionen 1. Erstellen Sie eine Wertetabelle für die Graphen der Funktionen, und zeichnen Sie den Graphen. a) y = 2x b) y = 3x c) y = 0,4x d) y = 0,8x 2. Ein Flugzeug verbraucht auf 200 km 1800 l Kerosin. a) Wie lautet die Funktionsgleichung, die den Verbrauch V abhängig von der Strecke s beschreibt? Definition einer Linearen Funktion Darstellung einer Funktion Parameter k und d: Graphische und Rechnerische Bestimmung Zeichnen von Linearen Funktionen Eigenschaften einer Linearen Funktion Aufstellen von Linearen Funktionen - Spezialfälle Lineare Gleichungssysteme graphisch lösen Zusätzlich: Erklärvideos (gratis!) zur visuellen Veranschaulichung.
AUFGABENSAMMLUNG - LINEARE GLEICHUNGEN & FUNKTIONEN Inhaltsverzeichnis Steigungsmessung von Geraden Lineare Gleichungen mit zwei Variablen Funktionen Lineare Funktionen Stückweise definierte Funktionen Proportionalitäten 2 4 8 12 20 23 Kompetenzmaterialien - Lineare Gleichungen & Funktionen Lineare Funktionen einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Lineare Funktionen Aufgaben mit Lösungen PDF Download
Lineare Funktion Definition: Die Funktion f: y = m·x + n; x є ℝ, nennt man lineare Funktion. Der Graph der linearen Funktion ist eine Gerade mit dem y-Achsenabschnitt n (absolutes Glied) und dem Steigungsfaktor (oder Proportionalitätsfaktor) m. Ganzrationale Funktion 1.Grades: Eine Funktion f(x) mit f(x) = a 1 x + a 0 und a 1 є ℝ, a 0 1 Übungsaufgaben 1. Welche der rechts abgebildeten Funktionsgraphen gehören zu linearen Funktionen, welche nicht? 2. Welche der folgenden Funktionsgleichungen gehören zu linearen Funktionen, welche nicht? a. 1( ) = d. 4( ) = 2 2 + 2




