Lineare Funktionen gehören zu den einfachsten Funktionstypen. Sie veranschaulichen einen linearen Zusammenhang zwischen der Definitionsmenge und dem Wertebereich . Du kannst diesen Zusammenhang immer in Form einer Gerade graphisch darstellen. In diesem Kapitel schauen wir uns an, was lineare Funktionen sind. Inhaltsverzeichnis Bestandteile Funktionsgleichung Definitionsmenge Wertemenge Graph y-Achsenabschnitt verändern Steigung verändern Ausnahme: Senkrechte Gerade Ausblick Erforderliches Vorwissen Was ist eine Funktion? Bestandteile

𝗦𝘁𝘂𝗱𝘆𝗴𝗿𝗮𝗺 𝗟𝗲𝗿𝗻𝘇𝗲𝘁𝘁𝗲𝗹 𝗶𝗣𝗮𝗱 on Instagram “Hey🙋🏼♀️ Heute gibt es den langersehnten Lernzettel
Lineare Funktionen Lineare Funktionen verwendet man, um Zusammenhänge zu beschreiben, bei denen etwas gleichmäßig zu- oder abnimmt, z.B. beim Befüllen von Wasserbecken, beim Abbrennen einer Kerze, bei Kosten für eine Taxifahrt oder einem Handytarif. Der Graph einer linearen Funktion ist eine Gerade im Koordinatensystem. lineare funktionen lernzettel Mathe 7 Lernzettel Kommentare (1) Cool, mit dem Lernzettel konnte ich mich richtig gut auf meine Klassenarbeit vorbereiten. Danke 👍👍 mathe zusammenfassung Ähnliche Inhalte 7 118 8 Mathe - Bestimmung der Funktionsgleichung Hier ist die Bestimmung der Funktionsgleichung in drei Schritten erklärt. Ich hoffe es hilft :) 1 Lineare Funktionen: Ablesen, Zeichnen Bruchrechnen mit Parametern und Variablen Anwendung: Prozentrechnen und Rechnen mit physikalischen Einheiten Quadratische Ergänzung Höhere Binome ( + ) ausmultiplizieren (binomischer Satz) Aufgabe 1: Ablesen von linearen Funktionen Welche (linearen) Funktionen gehören zu den folgenden Funktionsgraphen? Lineare Funktionen SKRIPT (14 Seiten) Theoretische Erklärungen und Beispielaufgaben zu folgenden Themenbereichen: Definition einer Linearen Funktion Darstellung einer Funktion Parameter k und d: Graphische und Rechnerische Bestimmung Zeichnen von Linearen Funktionen Eigenschaften einer Linearen Funktion

Lineare Funktionen Arbeitsblatt Pdf
Im Allgemeinen haben lineare Funktionen immer die folgende Gestalt: y = m ⋅ x + b. Wir notieren, dass m die Steigung und b den Schnittpunkt der Geraden mit der y -Achse angibt. Beachte: Im Regelfall werden Funktionen immer f ( x) genannt. f ( x) ist nichts anders als der Funktionswert, also y. LF1 Lineare Funktionen Thema: Graph und Funktionsgleichung LF 1 ©U. Roder 1 Lineare Funktionen Lineare Funktionen verwendet man, um Zusammenhänge zu beschreiben, bei denen etwas gleichmäßig zu- oder abnimmt, zum Beispiel das Abbrennen einer geraden Kerze oder die Kosten für eine Taxifahrt. Der Graph einer linearen Funktion ist eine Gerade im Eine lineare Funktion ist eine Funktion mit konstanter Steigung der Form: y=mx+t Dabei gibt m die Steigung an je größer m ist, desto steiler steigt/fällt die Funktion ist m positiv, steigt die Funktion ist m negativ, fällt die Funktion t den y-Achsenabschnitt. (also den Schnittpunkt mit der y-Achse) Jetzt sind lineare Funktionen einfach erklärt: Bei diesem Funktionstyp kommt die Variable x im Funktionsterm immer nur in der ersten Potenz vor. Deshalb nennt man sie auch Funktionen ersten Grades. Eine lineare Funktion sieht also zum Beispiel so aus: \(f(x) = 2x + 5\) Allgemein schreibt man die Funktionsgleichung einer linearen Funktion so:
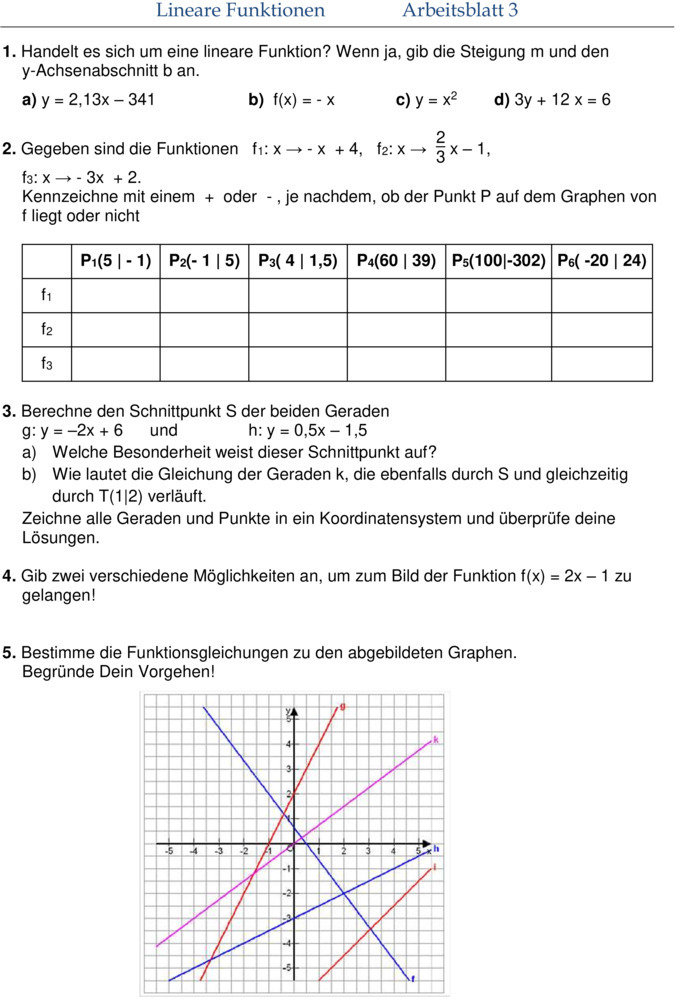
Lineare Funktionen Aufgaben Klasse 9 Hauptschule / Klassenarbeiten und Übungsblätter Mathematik
Jede lineare Funktion kannst du mathematisch als Gerade oder als Gleichung darstellen. Die Gleichung nennst du dann die Funktionsgleichung. Funktionsgleichung: m x + b Lineare Funktionen Lineare Funktionen Algebra 2x2 Matrix Determinante Addition Additionstheoreme Additionsverfahren Antiproportionale Zuordnung Arten von Gleichungen Assoziativgesetz Ausklammern und Ausmultiplizieren Besondere Matrizen Betrag und Gegenzahl Binomische Formeln Biquadratische Gleichungen Bruch in Dezimalzahl Brucharten
Eine lineare Funktionsgleichung hat die Form y = mx + t oder f (x) = mx + t y = die abhängige Variable: Es ist der Funktionswert, der davon abhängt, welchen Wert man für x einsetzt. m = Steigung m > 0: Die Gerade steigt, die Steigung ist positiv. m < 0: Die Gerade fällt, die Steigung ist negativ. a) Beschreibe das Monotonieverhalten der Funktion f. Begründe. _____ (2 P) b) Gib den y-Achsenabschnitt der Funktion f an. _____ (1 P) c) Liegt der Punkt P( -6 | 27) auf dem Graphen der Funktion f? Begründe. (2 P) d) Der Graph der Funktion h soll parallel zum Graphen der Funktion f verlaufen. Gib den Anstieg der linearen Funktion h an.

Die allgemeine lineare Funktion YouTube
Arbeitsblatt: Lineare Funktionen Zeichne den Funktionsgraphen der folgenden linearen Funktionen. a) f(x) = 2x − 3 b) f(x) = −1 x + 2 2 c) f(x) = x + 1 d) f(x) = 2,5x e) f(x) = 3 − x f) f(x) = 5 x − 1 3 2 g) f(x) e-Funktion Exponentialfunktionen exponentielles Wachstum und Zerfallsprozesse Extrempunkte Extremwertaufgaben Fläche zwischen der x-Achse und einem Graphen Fläche zwischen zwei Graphen Funktionsscharen Grenzwerte Hauptsatz der Differential und Integralrechnung Integralrechnung Kurvendiskussion lineare Funktionen Monotonie




