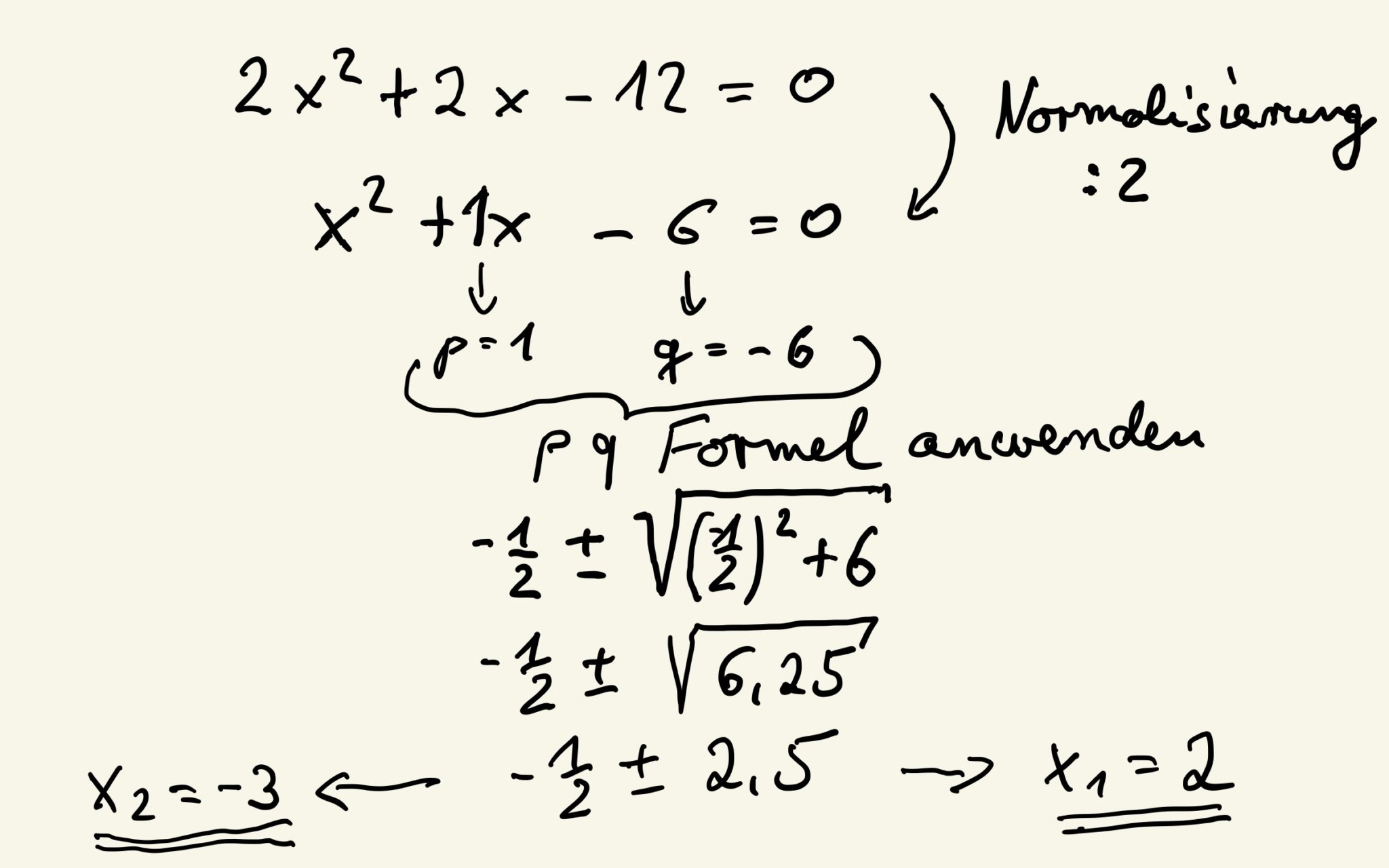pq Formel einfach erklärt Du möchtest eine quadratische Gleichung lösen, die so aussieht? x 2 + 2 x -3 =0 Dafür brauchst du die pq-Formel : pq Formel In die pq Formel kannst du dann einfach die Zahlen aus deiner Gleichung einsetzen. Dabei nimmst du für p die Zahl, die vor dem einzelnen x steht und für q die Zahl ohne x: Die pq-Formel ist eine Lösungsformel für quadratische Gleichungen in Normalform. Es gibt vier Arten von quadratischen Gleichungen in Normalform: Grundsätzlich können wir die pq-Formel auf alle vier Arten anwenden.

PQFormel Erklärung und Beispiele
Die Pq-Formel kann verwendet werden, um quadratische Funktionen oder quadratische Gleichungen zu lösen. Quadratische Gleichungen besitzen immer mindestens ein x², aber keine höheren Potenzen wie x³ oder x4. Damit du eine Aufgabe mit der pq-Formel lösen kannst, brauchen wir noch die entsprechende Formel. Wie lautet die pq-Formel? 1. Gleichung in Normalform bringen Bei x2 + 4x + 3 = 0 hast du schon eine Normalform. Du kannst Schritt 1 also überspringen . Anders sieht es bei diesen Beispielen aus: x2 + 4x = -3 → hier musst du zuerst die -3 auf die andere Seite bringen. Rechne dazu auf beiden Seiten +3. 2x2 + 4x + 3 = 0 → hier steht eine Zahl vor dem x 2. Die pq-Formel zur Lösung quadratischer Gleichungen - lernen mit Serlo! Die pq-Formel zur Lösung quadratischer Gleichungen Zur Lösung quadratischer Gleichungen kann man die pq-Formel benutzen. Dieser Artikel erklärt dir mit anschaulichen Beispielen, wie man die pq-Formel verwendet. Eine Erklärung samt Formel, wozu man die PQ-Formel überhaupt braucht anhand von Text und Grafiken. Es werden Beispiele mit Zahlen vorgerechnet und erläutert. Ihr bekommt Aufgaben bzw. Übungen zum selbst Rechnen mit Musterlösungen. Wer mag kann auch gleich mit den Aufgaben loslegen. Einige Videos mit weiteren Erklärungen zur PQ-Formel.
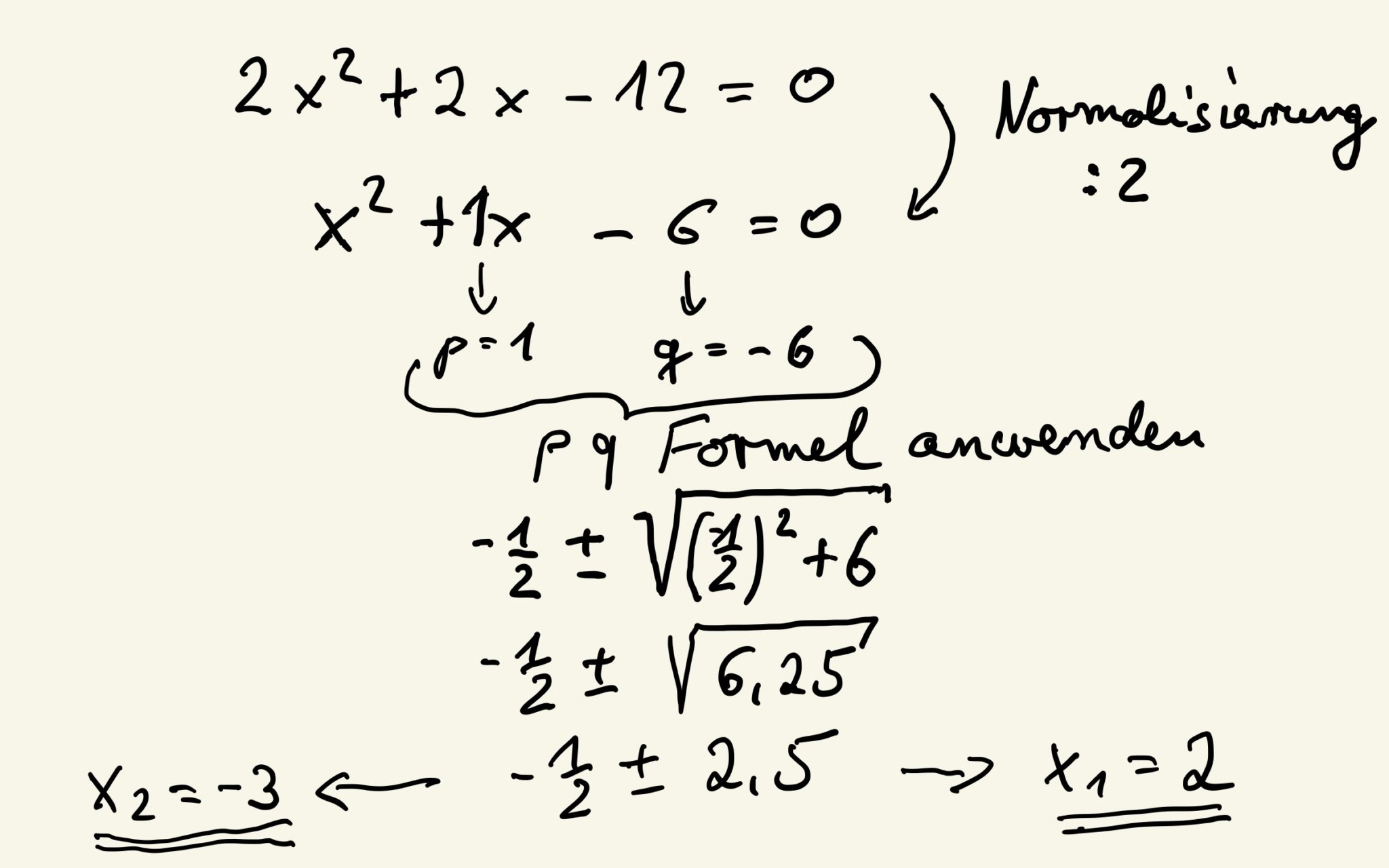
PQFormel Nullstellen Quadratischer Gleichungen berechnen Mathematik Nachhilfe
Mit p-q-Formel lassen sich quadratische Gleichungen der Form: leicht lösen. Die p-q-Formel besagt, dass es maximal zwei Lösungen für solche Gleichungen gibt, und zwar: Die Kombination aus Plus und Minus vor der Wurzel besagt dabei, dass die Wurzel für die eine Lösung addiert und für die andere Lösung subtrahiert werden muss. pq-Formel anwenden: Erklärung, Aufgaben & Beispiel Mathe Analysis pq-Formel pq-Formel Algebra 2x2 Matrix Determinante Addition Additionstheoreme Additionsverfahren Antiproportionale Zuordnung Arten von Gleichungen Assoziativgesetz Ausklammern und Ausmultiplizieren Besondere Matrizen Betrag und Gegenzahl Binomische Formeln Biquadratische Gleichungen Die PQ-Formel zum Lösen quadratischer Gleichungen wird in diesem Video behandelt. Dabei wird zunächst erklärt, was eine quadratische Gleichung (Funktion) übe. Die pq-Formel. Die -Formel lautet: Diese Schreibweise ist vielleicht ungewohnt, bedeutet aber lediglich: Die Lösungen und für eine Gleichung der Art sind: Von Schüler*innen wird nicht verlangt mit imaginären Zahlen zu rechnen. Sollte unter der Wurzel also eine negative Zahl stehen, könnt ihr für diese Lösung annehmen, dass die -Formel.

pq Formel • Erklärung, Herleitung, Beispiel · [mit Video]
Wie löst man eine gemischt-quadratische Gleichung? Was ist die Normalform? Warum ist die Normalform wichtig? Wie muss ich vorgehen? Wie kann ich mir einen Ar. Um dies zu erreichen, wird durch 3 dividiert. Danach werden p und q abgelesen. Die Zahlen von p und q werden in die PQ-Gleichung eingesetzt. Danach wird der Ausdruck vor und unter der Wurzel berechnet. Anschließend wird die Wurzel aus dem Wert gezogen und es wird einmal addiert und einmal subtrahiert. Eine quadratische Gleichung hat maximal.
Mit der pq-Formel kannst du Nullstellen von quadratischen Funktionen bestimmen. x_ {1,2} = -\dfrac {p} {2} \pm \sqrt {\left (\dfrac {p} {2}\right)^2-q} x1,2 = −2p ± (2p)2 − q Erklärung Eine quadratische Funktion hat die normierte Form: f (x) = x^2 + px+q f (x) = x2 +px+ q Hierbei sind p p und q q irgendwelche reelle Zahlen. Die pq-Formel ist ein nützliches Werkzeug, um quadratische Gleichungen zu lösen. Welche Voraussetzungen es gibt, wie sie sich herleitet und wie sie am Beispi.
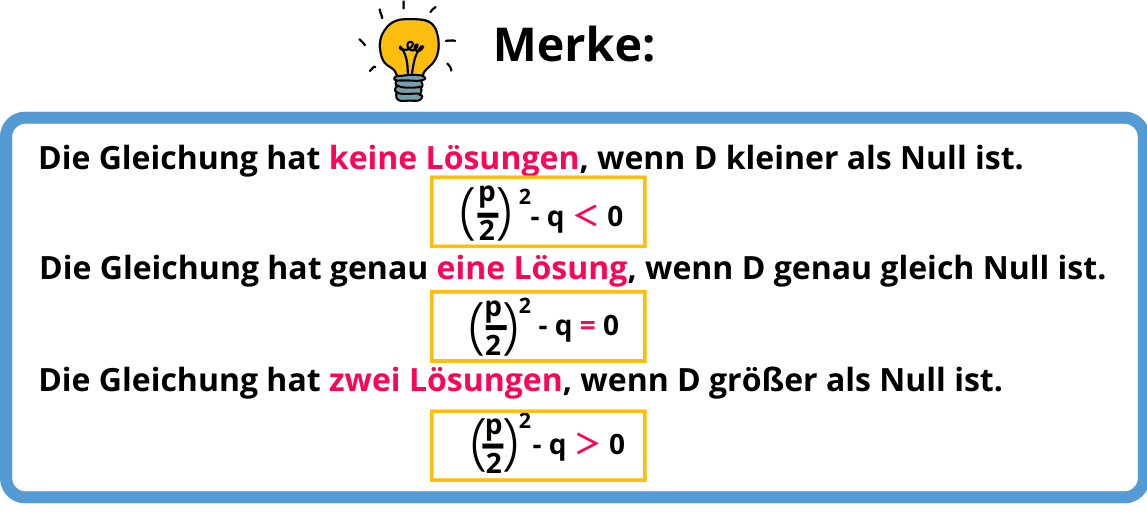
pqFormel Einfache Erklärung mit Beispielen
Die Quadratische Ergänzung / pq-Formel − eine Übersicht Die Quadratische Ergänzung ist ein Verfahren zum Lösen von Quadratischen Gleichungen und zur Bestimmung des Scheitelpunktes von quadratischen Funktionen. Dies wird im folgenden am Beispiel der quadratischen Funktion f(x) = 2x2 - 6x + 1 gezeigt. Die pq-Formel kann an quadratische Gleichungen zur Berechnung der Nullstellen angewendet werden. Diese muss zuvor in die Normalform gebracht werden. Eine Gleichung der Form x^ {2} + px + q = 0 x2 +px+ q = 0 kann mit der pq-Formel gelöst werden. Dafür werden die Werte p p und q q in folgende Formel eingesetzt.