Wir berechnen damit die Grundfläche unten wie folgt: Um das Volumen zu berechnen, müssen wir die Grundfläche noch mit der Höhe multiplizieren: Dieses Prisma hat ein Volumen von 420 Kubikzentimeter. Beispiel: Quader als Prisma. Wir haben ein Prisma, welches auch ein Quader ist. Es ist 14 Zentimeter hoch, 12 cm breit und 16 cm tief. Um den Flächeninhalt der Prisma Grundfläche zu berechnen, brauchst du die entsprechende Formel . Dann kannst du deine Werte einsetzen. G = ¼ · a 2 · G = ¼ · (3 cm) 2 · = ¼ · 9 cm 2 · ≈ 3,9 cm 2. 2. Mantelfläche ermitteln: Die Prisma Mantelfläche kannst du aus dem Umfang der Grundfläche U G und der Prisma Höhe h bestimmen. M = U.

Einstellung verkaufen Sich ausruhen prisma mantel berechnen Phänomen Pfad Gemacht, um sich zu
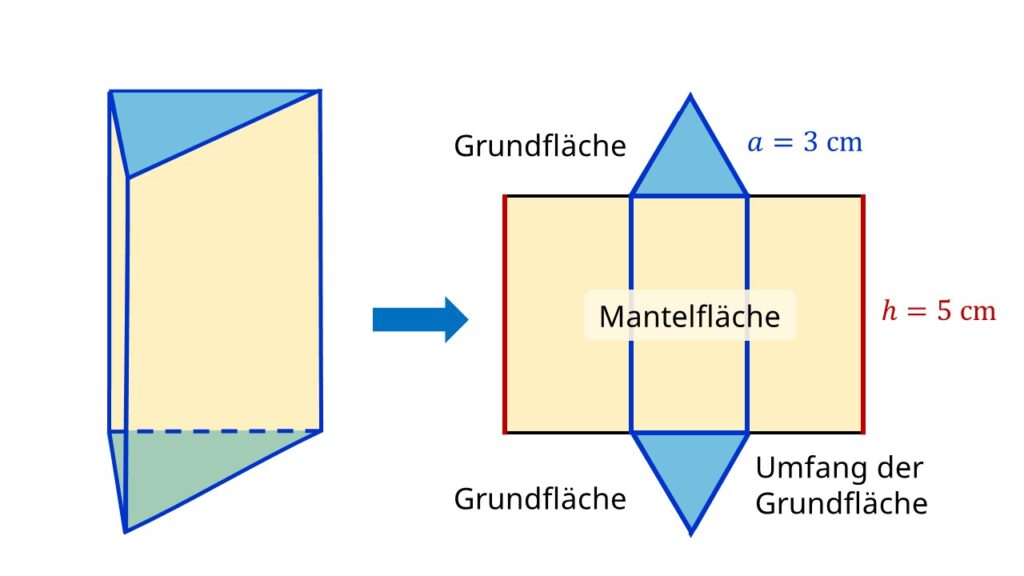
Wie rechnet man an einem Prisma? Es gelten folgende Rechenregeln: Das Volumen ist gleich Grundfläche*Höhe. Die Mantelfläche ist gleich (Umfang Grundfläche)*Höhe. Die Oberfläche ist gleich 2*Grundfläche+Mantelfläche. Alle diese Formeln sind leicht verständlich. Wenn du das Prisma zu einem Netz ausklappst, kannst du alle Flächen gut erkennen: Du siehst die Mantelfläche und zweimal die Grundfläche. Berechne die Grundfläche. Berechne die Mantelfläche. Berechne: Oberfläche = = 2 ⋅ ⋅ Grundfläche + + Mantelfläche. Kurzschreibweise: O = 2 ⋅ G + M O = 2 ⋅ G + M. Das Prisma besteht aus zwei gleichlaufenden Grundflächen und dem Mantel. Der Rechner führt die Berechnungen im rechteckigen regelmäßigen Prisma durch. Das rechteckige Prisma hat die Seitenflächen im rechten Winkel zu der Grundfläche. Das regelmäßige Prisma, ist ein Prisma, dessen Grundfläche alle Seiten gleich lang hat. Prisma Bei einem liegenden geraden Prisma erkennt man die Höhe nur dann als eine "Höhe", wenn man sich das Prisma auf die Grundfläche aufgestellt denkt.. Um den Oberflächeninhalt eines Prismas zu berechnen, muss man . zum Mantelflächeninhalt noch den Inhalt der Grund- und der Deckfläche addieren.

Volumen, Oberfläche und Mantelfläche bei einem Prisma YouTube
Trapezprisma. Schritt für Schritt kannst du auch das Volumen vom Trapez Prisma berechnen.Dafür sind die Seitenlängen a = 5 cm und c = 11 cm, sowie die Höhe der Grundfläche h T = 6 cm und die Höhe vom Prisma h P = 7 cm gegeben.. 1. Grundfläche herausfinden: Diesmal ist die Grundfläche ein Viereck mit zwei parallelen Seiten a || c. Somit brauchst du für das Volumen die Trapez Formel . So berechnest du das Volumen eines Prismas: Berechne die Grundfläche. Berechne das Volumen. Volumen = = Grundfläche ⋅ ⋅ Körperhöhe. Kurzschreibweise: V = G ⋅ hk V = G ⋅ h k. Ein Einheitswürfel hat die Kantenlänge a = 1 a = 1 cm c m und somit das Volumen V = 1 V = 1 cm3 c m 3. Das Volumen wird in cm3 c m 3 (sprich: Kubikzentimeter. Fünfeckiges Prisma - Oberfläche berechnen. Die Grundfläche hat hier eine Größe von 15 cm 2 und die Mantelfläche beträgt 150 cm 2 . Einsetzen liefert: O Prisma = 2 · A Grundfläche + A Mantelfläche = 2 · 15 cm 2 + 150 cm 2 = 180 cm 2. Das ergibt also einen Oberflächeninhalt von 180 cm 2. Prisma mit Dreieck ABC als Grundfläche ( h c = 16 cm, c = 42 cm) und einer Höhe h von 84 cm Grundfläche G (in cm 2): Volumen V (in cm 3): Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen eines Prismas berechnen.

Volumen Berechnen
In der Mathematik werden Prismen nach ihrer Seite benannt: Also unterscheidet man zwischen dreiseitigem, vierseitigem und vielseitigem Prisma.Wie man das Vol. Als nächstes berechnen wir die Mantelfläche. Dazu benötigen wir den Umfang der Grundfläche. Die Längen der Katheten haben wir, fehlt also noch die Länge der Hypotenuse. Die Summe dieser drei Längen ist dann der Umfang der Grundfläche des Prisma. Diesen Wert multiplizieren wir mit der Höhe um A M zu erhalten.
Formel für die Berechnung der Mantelfläche: Umfang der Grundfläche mal Höhe des Prismas (siehe oben). Der Umfang der Grundfläche ist die Summe von deren Seitenlängen. Beispielberechnungen: 1) Prisma mit Grundfläche Quadrat (Seitenlängen je 5 cm) und Kantenhöhe 10 cm. sechsseitiges Prisma. Ein sechsseitiges Prisma ist ein mathematischer Körper. Seine Grund- und Deckfläche bildet jeweils ein gleich großes regelmäßiges Sechseck. Seine 6 Seitenflächen sind rechteckig und ebenfalls alle gleich groß. Es besteht also insgesamt aus 8 Flächen.
Oberfläche Prisma • Mantelfläche Prisma, Grundfläche Prisma · [mit Video]
Prisma, fünfseitig. Ein fünfseitiges Prisma ist ein mathematischer Körper. Seine Grund- und Deckfläche bildet jeweils ein gleich großes regelmäßiges Fünfeck. Seine 5 Seitenflächen sind rechteckig und ebenfalls alle gleich groß. Es besteht also insgesamt aus 7 Flächen. Seine 15 Kanten bilden zusammen 10 Ecken. Prisma berechnen. Dieser Prismen-Rechner berechnet die drei Grundkanten, Umfang, Grundfläche, Höhe, Mantelfläche, Oberfläche und Volumen eines geraden Prismas mit dreieckiger Grundfläche, wenn vier geeignete Größen vorgegeben sind. Eingabedaten (4 Größen vorgeben, davon 2 Grundkanten) Titel (optional): 1. Grundkante:




