Aufgabe 1: Trage die richtigen Begriffe ein. Quadratische Funktionen haben eine quadrierte Variable (x²). Die einfachste (tschiraquade) Funktion hat die Gleichung y = x². Ihr Graph heißt (paraNormablle). Die Normalparabel verläuft symmetrisch zu der Achse, durch die das (Minumim) verläuft. Aufgaben zu quadratischen Funktionen 1 Bestimme jeweils die Scheitelform der unten abgebildeten Parabeln. Lösung anzeigen 2 Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen. Der Graph der Funktion verläuft durch die Punkte A (1|1), B (3|4), C (5|-1) Lösung anzeigen
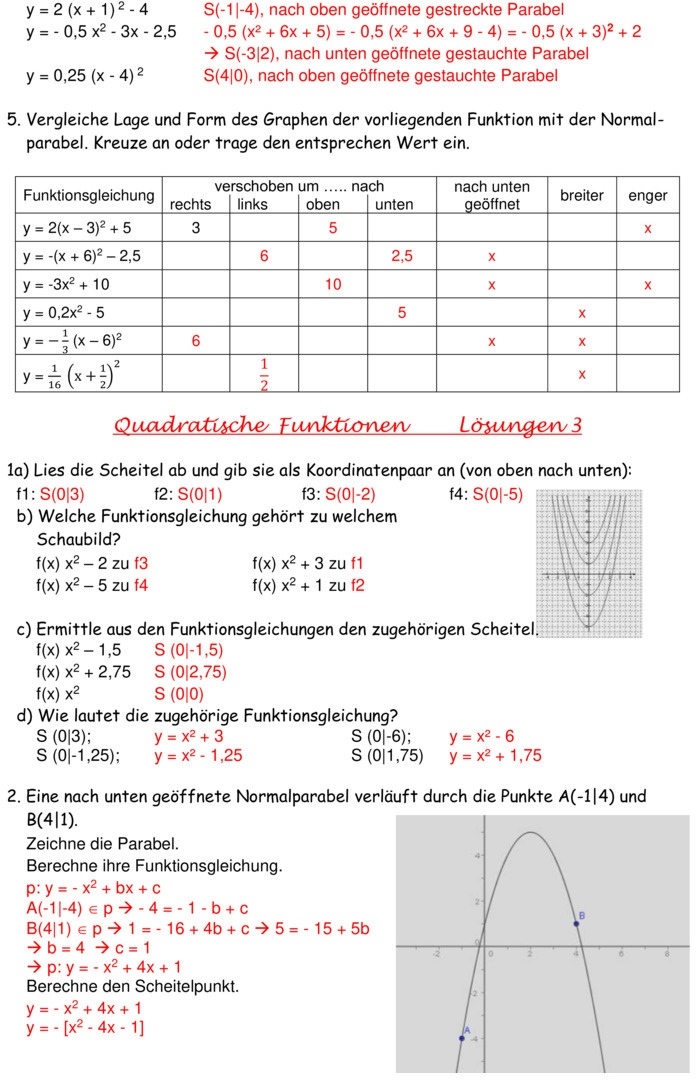
Übungsblatt zu Quadratische Funktionen
Quadratische Funktion Eine Funktion mit der Gleichung f(x) = ax 2 + bx + c heißt quadratische Funktion. Beispiel: y = 0,5 (x - 2) 2 + 3 Die Parabel der Funktion mit y = 0,5 (x - 2) 2 + 3 ist gegenüber dem Graphen der speziellen quadratischen Funktion mit y = 0,5 x 2 um 2 nach rechts und um 3 nach oben verschoben; der Scheitel liegt bei S. Quadratische Funktionen, Gemischte Aufgaben Klassenarbeit 4477 Quadratische Funktionen Neuigkeiten Neue Übungsblätter für Mathematik Klassenstufe 4. 03. September 2023 Übungsblatt mit Musterlösung zu Quadratische Funktionen [10. Klasse], Quadratische Funktionen; Gemischte Aufgaben. Das Wachstum der Zellkultur kann durch eine quadratische Funktion beschrieben werden. Berechne die Funktionsgleichung und zeichne den Graphen in ein geeignetes Koordinatensystem. Lösung anzeigen Quadratische Funktionen einfach erklärt Viele Mathematik-Themen Üben für Quadratische Funktionen mit interaktiven Aufgaben, Übungen & Lösungen.
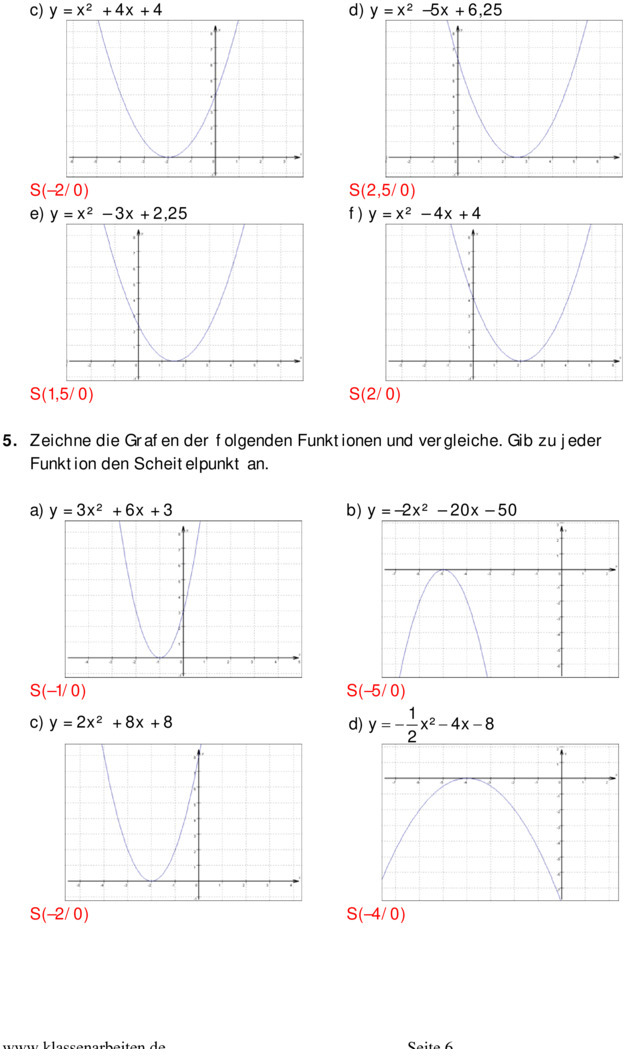
Übungsblatt zu Quadratische Funktionen [10. Klasse]
Quadratische Funktionen - Textaufgabe Der Bogen einer Hängebrücke von der Form einer Parabel verläuft gemäß dem Graphen der Funktion $f(x) = -0,004x^2+1,2x-32,4$. Die Verankerungspunkte der Brücke liegen unterhalb der durch die x-Achse markierten Straße. Eine quadratische Funktion erkennst du daran, dass ein x2 vorkommt, aber kein x 3, x 4, x 5, usw… Der Graph einer quadratischen Funktion ist eine Parabel . Hier siehst du den Graphen der einfachsten quadratischen Funktion f (x) = x2. Den nennst du Normalparabel. Normalparabel Der Scheitelpunkt S ist der tiefste oder höchste Punkt einer Parabel. 8 Aufgaben: Zeichnen quadratischer Funktionen 12 Aufgaben: Bestimmung des Scheitelpunkts 12 Aufgaben: Bestimmung des Scheitelpunkts 12 Aufgaben: Bestimmen der Funktionsgleichung aus dem Scheitelpunkt und einem weiteren Punkt des Graphen 4 Aufgaben: Bestimmen der Funktionsgleichung aus frei gegebenen Punkten des Graphen Lerne wie du quadratische Gleichungen löst und wie du quadratische Funktionen analysierst und graphisch darstellst. Lerne wie du quadratische Gleichungen löst und wie du quadratische Funktionen analysierst und graphisch darstellst. If you're seeing this message, it means we're having trouble loading external resources on our website. Wenn du hinter einem Webfilter bist, stelle sicher, dass.

Aufgaben Quadratische Gleichungen mit Lösungen Koonys Schule 0060
Eine Funktion f mit der Funktionsgleichung f ( x) = a x 2 + b x + c heißt quadratische Funktion. Wegen y = f ( x) können wir statt f ( x) = a x 2 + b x + c auch y = a x 2 + b x + c schreiben. Charakteristische Eigenschaft Im Funktionsterm quadratischer Funktionen kommt x in der 2. Potenz, aber keiner höheren Potenz vor. Quadratische Funktionen - einführende Aufgaben mit a≠1 Gestreckte und gestauchte Parabeln, Bestimmung von Parametern (insbesondere Formparameter) anhand des Grafen, leichte Scheitelbestimmung Formfaktor Parabel quadratische Funktionen Scheitelpunkt 39 Aufgaben, 6 Levels Quadratische Funktionen - einführende Aufgaben mit a=1
Lösungsblatt: Quadratische Funktionen Version vom 28. April 2020 1 Es gibt zu allen Aufgaben unendlich viele Lösungen. Zur Kontrolle kann bei GeoGebra der Funktionsgraph betrachtet werden. 2 a) f(x) = 1 4 ·(x−1)2 +2 b) f(x) = −1 8 ·(x+2)2 +3 c) f(x) = 4 9 ·(x−4)2 −1 d) f(x) = 1 2 ·x 2 +1 3 a) f(x) = −0,2x2 +0,8x+1 b) f(x) = 0. Minimum y S. Bei einer nach oben geöffneten Parabel liegt ein Minimum, bei einer nach unten geöffneten Parabel ein Maximum vor. Eine Parabel mit der Gleichung y = ax² + bx + c ( Allgemeine Form) und dem Scheitel S (s ; t) lässt sich auch durch die Gleichung y = a (x − s)² + t ( Scheitelpunktform) ausdrücken.
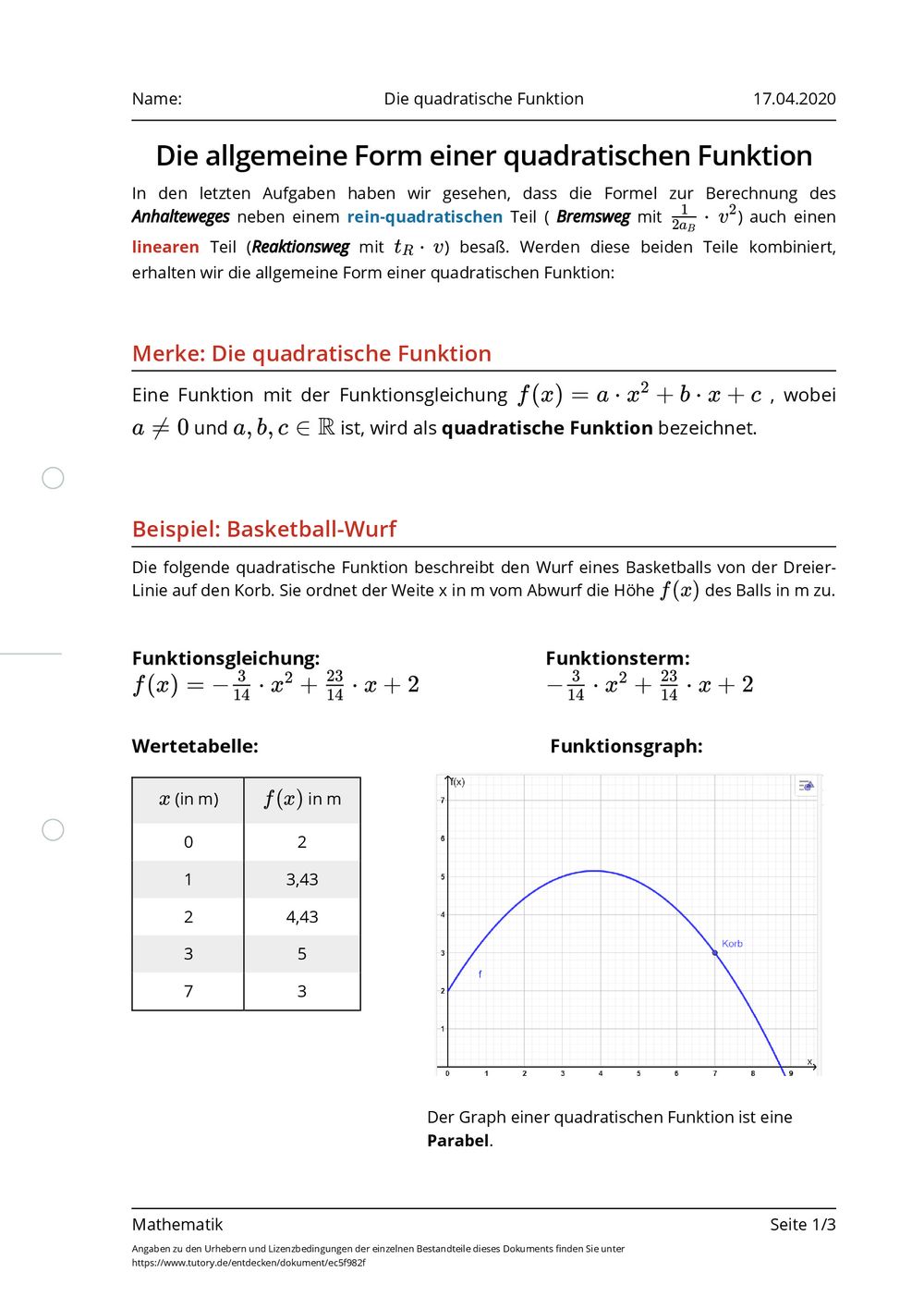
Arbeitsblatt Die quadratische Funktion Mathematik tutory.de
Aufgaben zum Aufstellen quadratischen Funktionen 1 Bestimme jeweils die Scheitelform der unten abgebildeten Parabeln. Lösung anzeigen 2 Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen. Der Graph der Funktion verläuft durch die Punkte A (1|1), B (3|4), C (5|-1) Lösung anzeigen Hier findest du gemischte Aufgaben zum Thema quadratischen Funktionen. Schaffst du sie alle? 1 Welche Werte kann der Parameter t annehmen, so dass die folgenden Aussagen richtig sind? Der Graph der Funktion f mit f\left (x\right)=x^2+tx+1 f (x) = x2 + tx +1 verläuft vollständig oberhalb der x-Achse. Lösung anzeigen




