Mit der Scheitelpunktform kannst du jede quadratische Funktion als Parabel darstellen. Sie hat die Form. f (x) = a (x - d)2 + e. Den Scheitelpunkt kannst du daran direkt ablesen, er lautet: S (d|e) . a ist ein Faktor, der die Steilheit der Parabel angibt. Beispiel: Der Scheitelpunkt der Funktion f (x) = 2 (x - 3)2 + 1 liegt bei S (3|1). f ( x) = x 2 + p x + ( p 2) 2 − ( p 2) 2 = ( x + p 2) 2 − ( p 2) 2. Beispiel 2. Gegeben sei die quadratische Funktion. f ( x) = 3 x 2 + 6 x + 7. Berechne den Scheitelpunkt mithilfe der quadratischen Ergänzung. Koeffizient von x 2 aus x 2 und x ausklammern. f ( x) = 3 ⋅ ( x 2 + 2 x) + 7.
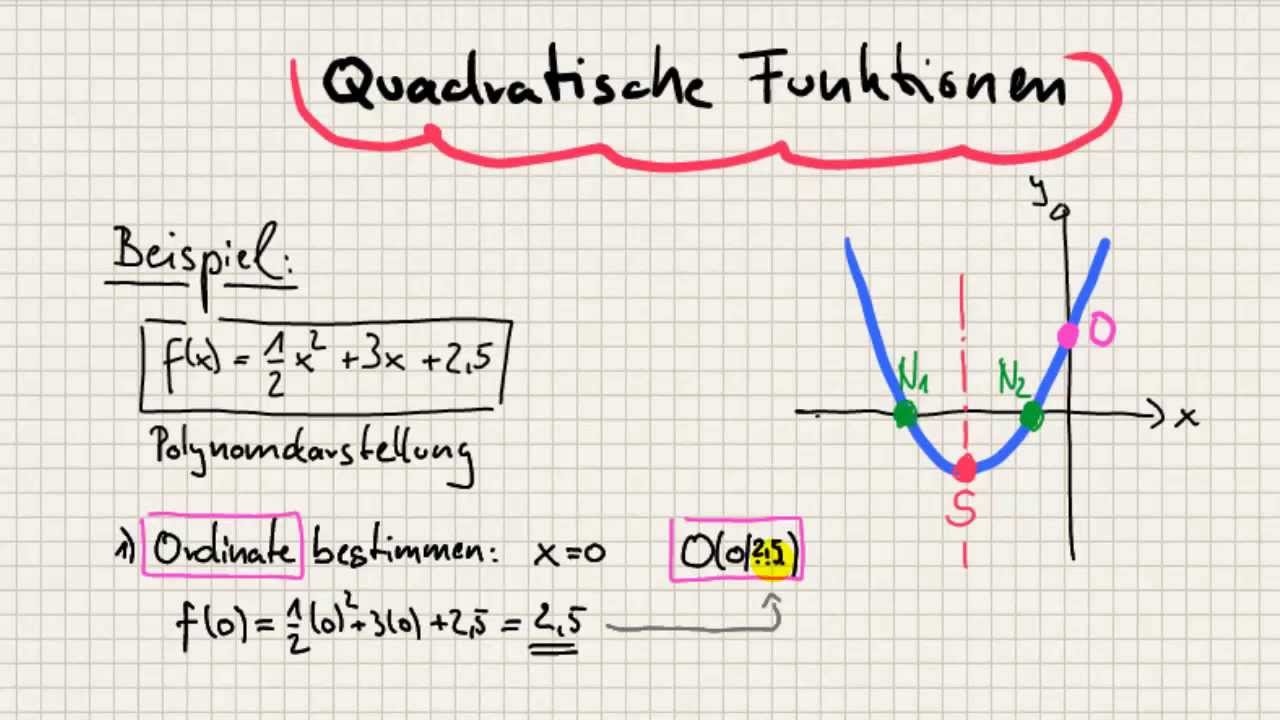
Quadratische Funktionen Ordinate, Nullstellen, Scheitel und Skizze YouTube
Wann Du welche Form benutzt, hängt davon ab, ob Du die Nullstellen oder den Scheitelpunkt einer quadratischen Funktion ermitteln möchtest. Zur Erinnerung: Der Graph von quadratischen Funktionen nennt sich Parabel und ist entweder nach oben oder unten geöffnet. Die allgemeine Form einer quadratischen Funktion ist $f (x) = ax^2 + bx +c$. Definition. Unter der Scheitelpunktform (kurz: Scheitelform) versteht man eine bestimmte Form einer quadratischen Gleichung, aus der man den Scheitelpunkt direkt ablesen kann: Die Scheitelpunktform ist eine spezielle Form der quadratischen Funktion. An der Scheitelpunktform kann man besonders schnell sehen, wo der höchste bzw. tiefste Punkt (der Scheitelpunkt) einer Parabel ist: Die Zahl in der Klammer gibt (Vorsicht: bis auf das Vorzeichen!) die x-Koordinate des Scheitelpunktes an, die Zahl ganz hinten die y. Quadratische Funktion. Scheitelpunktform. Scheitelpunkt quadratischer Funktionen - Verschieben der Normalparabel in x-Richtung. Manchmal ist es nötig, quadratische Funktionen der Form x² + px + q in eine andere Form umzurechnen, bei der man den Scheitelpunkt direkt ablesen kann.

Quadratische Funktionen Scheitelpunktform aus Grafik ablesen Übung 6 YouTube
Um von der Allgemeinform einer quadratischen Funktion auf die Scheitelpunktform zu kommen, verwendet man die quadratische Ergänzung. Allgemein: f (x) = a·x 2 + b·x + c. | Quadratische. | Ergänzung. Du kannst den Scheitelpunkt von quadratischen Funktionen auf verschiedene Weisen bestimmen. Zum Beispiel mithilfe. der Scheitelpunktform. der allgemeinen Form. der Ableitung. Der Scheitelpunkt einer quadratischen Funktion ist deren tiefster oder höchster Punkt. Hier lernst du, wie der Scheitelpunkt bestimmt wird und was man unter der Scheitelpunktform einer quadratischen Funktion versteht. Anschließend lernst du, die Scheitelpunktform aufzustellen. Beliebteste Videos und Lerntexte. + Interaktive Übung. Scheitelpunktform Die Scheitelpunkte von quadratischen Funktionen in Normalform werden mit einer einfachen Formel, ähnlich der pq Formel berechnet. In diesem Beitrag wird an drei Aufgaben mit Lösungen gezeigt, wie's funktioniert. Aufgabe 1. Berechne den Scheitelpunkt der Funktion f (x) = x2 - 8x + 15. Lösung 1. p = -8, q = 15. -p/2 = 4 , -p2/4 + q = -16 + 15 = -1.

Scheitel bestimmen bei quadratischen Funktionen (Parabeln) Quadratische funktion, Mathematik
In diesem Video schauen wir uns die Umformung einer Funktionsgleichung in die Scheitelpunktform an. Die Scheitelpunktform hat nämlich einen wichtigen Vorteil: Man kann den Scheitelpunkt der. Berechne den Scheitelpunkt folgender Funktionen mithilfe der Formel. Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3). f ( x ) = x 2 + 6 x + 9 f(x) = x^2 + 6x + 9 f ( x ) = x 2 + 6 x + 9
Allgemein hat die Normalform einer quadratischen Funktion immer die Struktur ax2 + bx + c. Dabei kannst du für a, b und c verschiedene Zahlen wählen, wie oben im Beispiel 2, -4 und -2 . Die Scheitelpunktform zur Normalform 2x2 - 4x - 2 lautet: 2 • (x - 1)2 - 4. Allgemein erkennst du immer die Struktur a • (x - d)2 + e. Eine quadratische Funktion in der Scheitelpunktform sieht allgemein so aus: Merke. Für beliebige reelle Zahlen a, d und e mit a ungleich Null gilt: f(x) = a ⋅ (x −d)2 + e. Streckfaktor: a. Scheitelpunkt: S (d|e) Du kannst aus der Form direkt den Scheitelpunkt ablesen. Das a steht für den Streckfaktor. Gut zu wissen.
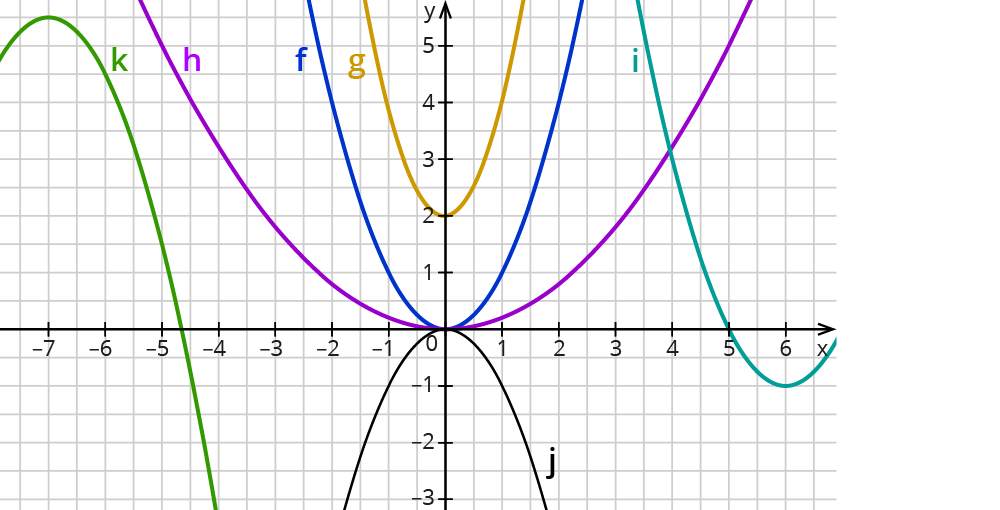
Eliminator Blog Scheitelpunkt Berechnen Mit Nullstellen
Hier siehst du den Graphen der einfachsten quadratischen Funktion f (x) = x2. Den nennst du Normalparabel. Normalparabel. Der Scheitelpunkt S ist der tiefste oder höchste Punkt einer Parabel. Bei einer Normalparabel liegt er im Punkt S (0|0). Du kannst eine quadratische Funktion verändern, indem du. Dafür nehme wir eine quadratische Funktion bzw. eine quadratische Gleichung, die in der Form für die PQ-Formel oder die ABC-Formel vorliegt. Auch hier sehen wir uns die Berechnung und Beispiele an.




