Interaktiver, gratis online Grafikrechner von GeoGebra: zeichne Funktionen, stelle Daten dar, ziehe Schieberegler, und viel mehr! Bei quadratischen Funktionen handelt es sich um ganzrationale Funktionen der Form f(x) = ax2 + bx + c, wobei a, b und c reelle Zahlen mit a ≠ 0 sind. Das bedeutet auch, dass es für jeden y-Wert (abgesehen von dem des Scheitelpunkts) zwei x-Werte gibt! Schauen wir uns als Beispiel die quadratische Funktion f(x) = 0, 5x2 − 4x + 6 an: Dies.
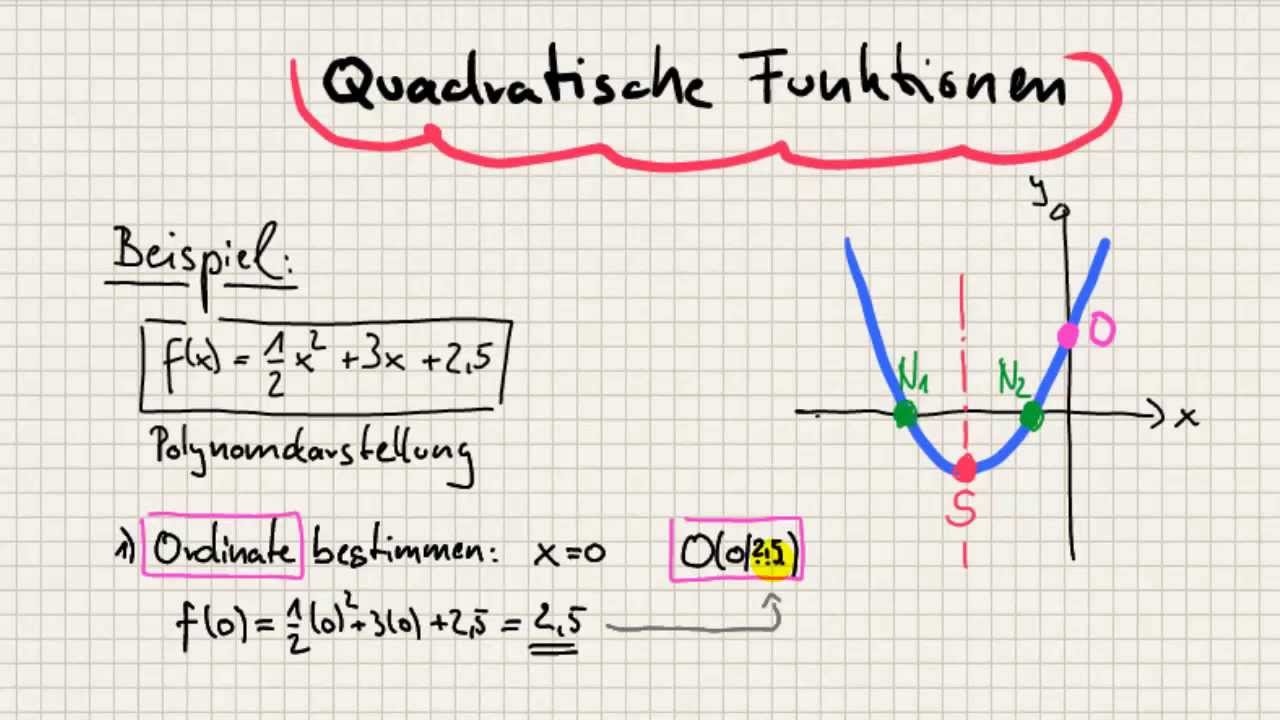
Quadratische Funktionen Ordinate, Nullstellen, Scheitel und Skizze YouTube
Quadratische Funktionen einfach erklärt Scheitelpunktform & Normalform Quadratische Funktionen Aufgaben mit kostenlosem Video. Parabel zeichnen Dauer: 04:37 Scheitelpunkt Dauer: 05:03 Gestreckte und gestauchte Parabel Dauer: 03:46 Nullstellen berechnen quadratische Funktion Zeichnen einer quadratischen Funktion. Wenn man die Funktionsvorschrift hat, ist es relativ einfach eine Funktion zu zeichnen. Das Vorgehen ist dabei dasselbe wie auch bei den linearen Funktionen. Zunächst einmal müssen wir eine Wertetabelle anlegen mit dem für uns relevanten Bereich. Anschließend können wir die Punkte in ein geeignetes. Entdecke Mathe mit unserem tollen, kostenlosen Online-Grafikrechner: Funktionsgraphen und Punkte darstellen, algebraische Gleichungen veranschaulichen, Schieberegler hinzufügen, Graphen animieren u.v.m. In diesem Artikel wiederholen wir, wie du eine quadratische Funktion zeichnest. Der Graph einer quadratischen Funktion ist eine Parabel, welche eine "u"-förmige Kurve darstellt: 2 4 − 4 2 4 − 4 y x. In diesem Artikel wiederholen wir, wie quadratische Funktionen gezeichnet werden. Suchst du eine Einführung in Parabeln?
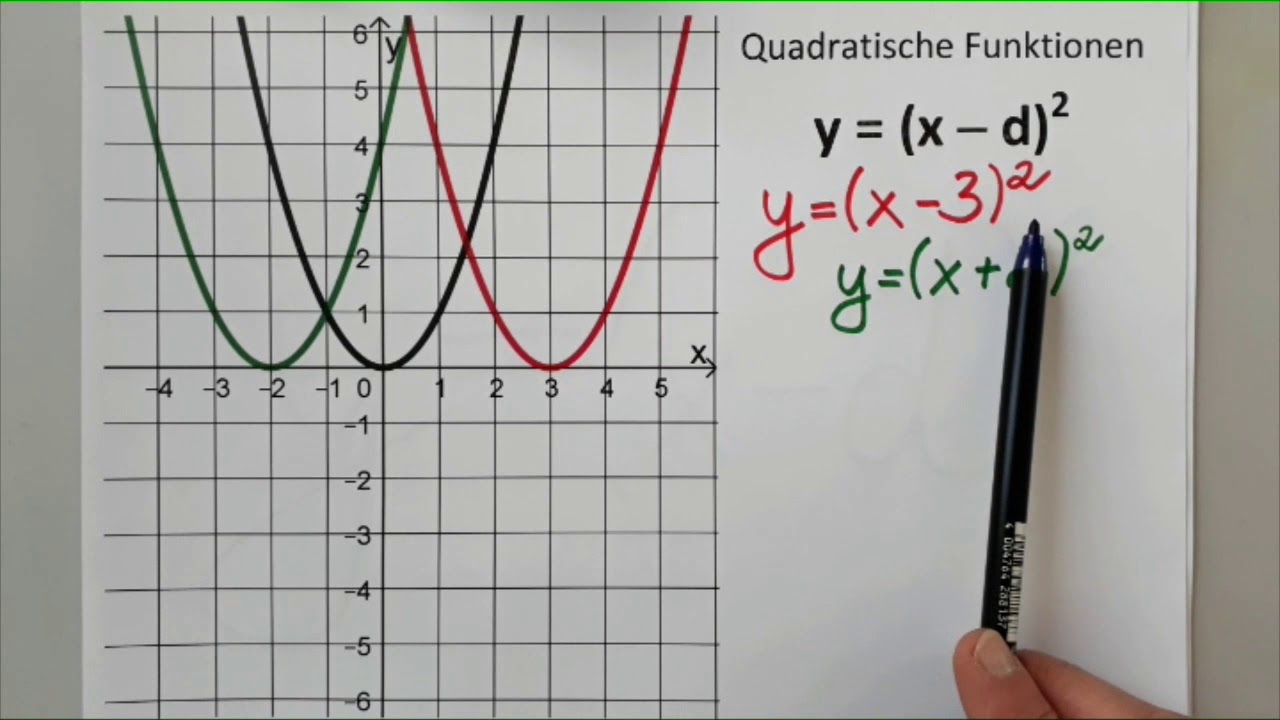
Quadratische Funktionen YouTube
Eine Funktion f mit der Funktionsgleichung. f ( x) = a x 2 + b x + c. heißt quadratische Funktion. Wegen y = f ( x) können wir statt f ( x) = a x 2 + b x + c auch y = a x 2 + b x + c schreiben. Charakteristische Eigenschaft. Im Funktionsterm quadratischer Funktionen kommt x in der 2. Potenz, aber keiner höheren Potenz vor. Get this widget. Added Nov 5, 2013 in Mathematics. A simple plotter-widget. Send feedback | Visit Wolfram|Alpha. Get the free "Funktionen zeichnen" widget for your website, blog, Wordpress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha. Lerne wie du quadratische Gleichungen löst und wie du quadratische Funktionen analysierst und graphisch darstellst.. Quadratische Gleichungen zeichnen - Wiederholung (Öffnet ein modal) Übe. Merkmale quadratischer Funktionen: Strategie Schaffe 3 von 4 Aufgaben, um ein höheres Level zu erreichen! Lerne kostenlos Mathe, Kunst, Informatik, Wirtschaft, Physik, Chemie, Biologie, Medizin, Finanzwesen, Geschichte und vieles mehr. Khan Academy ist eine Non-profit Organisation mit dem Zweck eine kostenlose, weltklasse Ausbildung für jeden Menschen auf der ganzen Welt zugänglich zu machen.

Quadratischen Funktionen zeichnen Übung 8
Um die Lage der Nullstellen zu bestimmen, muss man eine quadratische Gleichung lösen, z.B. mithilfe der Mitternachtsformel, bei der die Funktion gleich 0 0 0 gesetzt werden muss.. Scheitel. Als Scheitel einer Parabel bezeichnet man ihr Extremum.Es liegt immer bei x = − b 2 a x=-\frac b{2a} x = − 2 a b .. Man erhält den Scheitelpunkt einer Parabel entweder durch quadratische Ergänzung. Die Quadratischen Funktionen kann man besser verstehen, wenn man sie sich im Kopf vorstellen kann. Es ist wichtig den Scheitelpunkt zu kennen und man muss er.
Quadratische Funktionen Gemischte Aufgaben zu quadratischen Funktionen. Aufgaben zu Extremwerten. Aufgaben zum Zeichnen von Parabeln. Aufgaben zum Aufstellen quadratischen Funktionen. Dieses Werk steht unter der freien Lizenz.
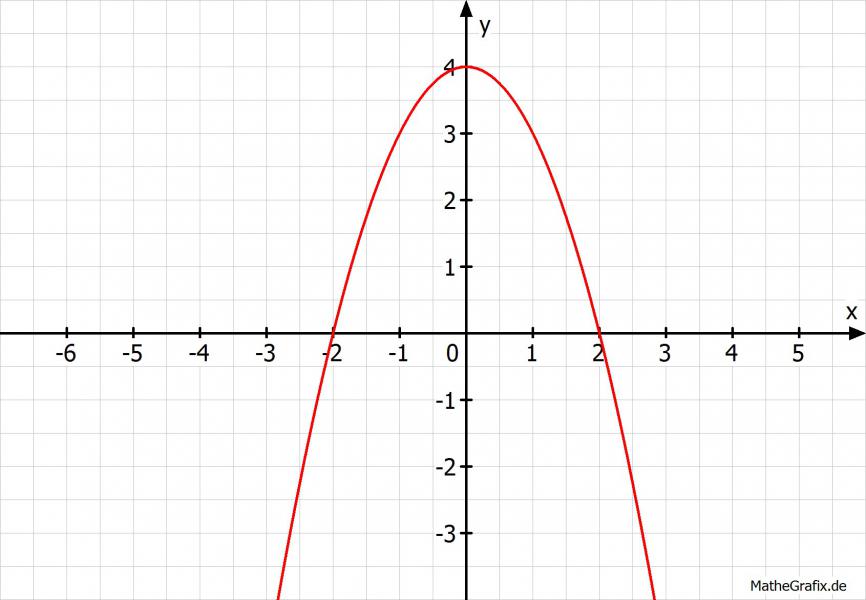
Zeichnen der quadratischen Funktion y = x^2+4 Mathelounge
Es ist wichtig, dass man sich die verschiedenen Parabeln im Kopf vorstellen kann. In diesem Video schauen wir uns das mal im Detail an! Wir werden die Parabe. Quadratische Funktionen - Einführung. Wir hatten bereits die linearen Funktionen kennengelernt und geklärt, wie f (x) = Formel mit x = y zu verstehen ist. Wir setzen für x einen Wert ein und die Formel berechnet den Wert für y. Wählen wir einen Wert mit x = 5 und setzen ihn in die Funktionsgleichung ein, so ergibt sich: Damit können wir.



