Wenn für die Seitenlänge der Grundfläche steht und für die Höhe der Pyramide (der senkrechte Abstand von der Grundfläche bis zur Spitze), dann kann das Volumen einer quadratischen Pyramide mit der Formel = errechnet werden. Es spielt keine Rolle, ob die Pyramide die Größe eines Briefbeschwerers hat oder größer als die Große Pyramide. Quadratische Pyramide: Höhe, Seite, Fläche und Volumen Sehen wir uns zunächst einmal an, wie eine gerade, quadratische Pyramide aussieht. Die nächste Grafik zeigt eine Pyramide mit einem Quadrat als Grundfläche.

Come Calcolare il Volume di una Piramide a Base Quadrata
Das Volumen (der Rauminhalt) der quadratischen Pyramide. Unter dem Volumen (oder auch Rauminhalt) eines Körpers versteht man den räumlichen Inhalt dieses Körpers. Umgangssprachlich würde man sagen: all jenes, das in diese Pyramide hineinpasst (Flüssigkeit,.) Das Volumen wird mit V abgekürzt und entspricht in der ebenen Geometrie dem. Bei einer quadratischen Pyramide beträgt die Länge der Grundkante $$8 m$$. Die Höhe der Pyramide beträgt $$6 m$$. Da die Grundfläche ein Quadrat ist, gilt für das Volumen: $$V_(Py)=1/3*G*h=1/3*8*8*6=128$$ Das Volumen der Pyramide beträgt $$128 m^3$$. Wir berechnen das Volumen einer quadratischen Pyramide. Die quadratische Pyramide ist ein Spitzkörper. Es gilt also die Formel V = 1/3 * G * hDa die Grundflä. Volumen der Pyramide berechnen. Die Formel für das Volumen der Pyramide lautet: V = 1/3 • G • h. Dabei ist G die Grundfläche und h die Höhe der Pyramide. Hast du zum Beispiel ein Quadrat mit Seitenlänge a als Grundfläche, dann rechnest du: V = 1/3 • a • a • h.

Como Calcular o Volume de uma Pirâmide Quadrada
Volumen V = 16 Neigung der Seitenflächen = 56,31° = 0,983 rad Neigung Seitenkante = 46,686° = 0,815 rad Seitenfläche A S = 7,211 Alle Pyramideformeln auf einen Blick Dies sind die notwendigen Formeln zum Berechnen einer quadratischen Pyramide: Link zur Grafik: https://www.matheretter.de/img/wiki/pyramide-formeln.png Was ist ein Pyramide? Berechne das Volumen der quadratischen Pyramide mit der Seitenlänge a = 3 c m und der Höhe h = 8 c m. Lösung. Um nun das Volumen berechnen zu können verwendest Du die Formel für die Berechnung des Volumens von Pyramiden und fügst als Grundfläche a 2 ein: 1.Schritt. Formel aufstellen: V = 1 3 · G · h = 1 3 · a 2 · h. 2.Schritt. Werte. In diesem Video lernst Du, wie man das Volumen einer quadratischen berechnet. Außerdem zeige ich Dir, wie Du die Höhe h und die Grundkante a bestimmen kannst. Das Volumen einer quadratischen Pyramide kann mit einer einfachen mathematischen Formel berechnet werden. Diese Formel, die als Volumenformel bezeichnet wird, lautet: Volumen = 1/3 * (Seitenlänge)2 * Höhe. Wenn einer der beiden Werte sich verändert, ändert sich auch das Volumen der Pyramide.
Volumen y Área de una Pirámide Cuadrada con Ejercicios Neurochispas
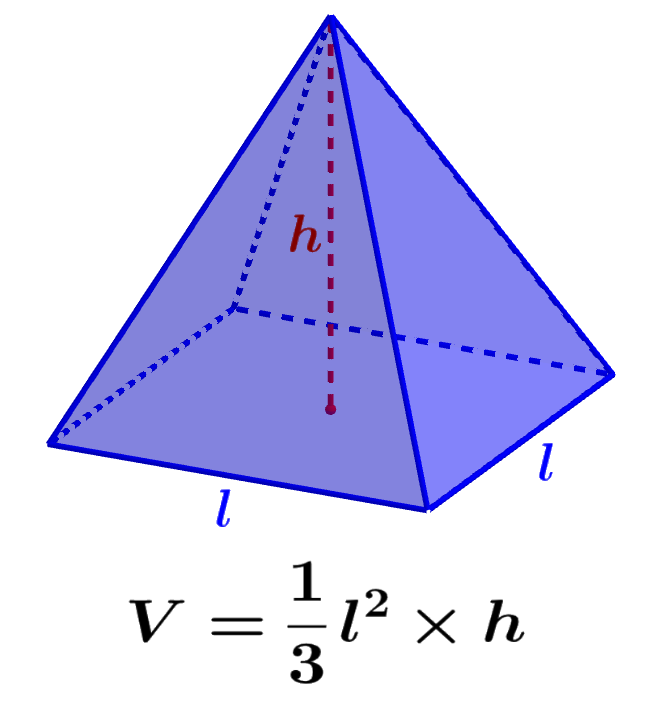
Volumen = (1/3) × Grundfläche × Höhe, wobei Höhe die Höhe von der Grundfläche bis zum Scheitelpunkt ist. Diese Formel gilt für alle Arten von Basispolygonen sowie für schräge und senkrechte Pyramiden. Alles, was du wissen musst, sind diese beiden Werte - Grundfläche und Höhe. Volumen einer Pyramide Folgendes Bild zeigt eine Pyramide mit quadratischer Grundfläche: Diese besteht aus einer quadratischen Grundfläche und vier gleichen, dreieckigen Seitenflächen, die oben spitz zusammenlaufen. Die Höhe h steht genau mittig und rechtwinklig auf der Grundfläche. Das Volumen berechnet sich folgendermaßen:
Unter allen quadratischen Pyramiden mit vorgegebener Oberfläche hat diejenige das größte Volumen, für die a = O 2 , h = O 2 {\displaystyle a={\frac {\sqrt {O}}{2}},\quad h={\sqrt {\frac {O}{2}}}\quad } und damit h = a ⋅ 2 {\displaystyle \quad h=a\cdot {\sqrt {2}}} Pyramide Pyramide Wichtige Inhalte in diesem Video Was ist eine Pyramide? (00:14) Sonderformen der Pyramide (01:01) Volumen Pyramide (02:21) Oberfläche Pyramide
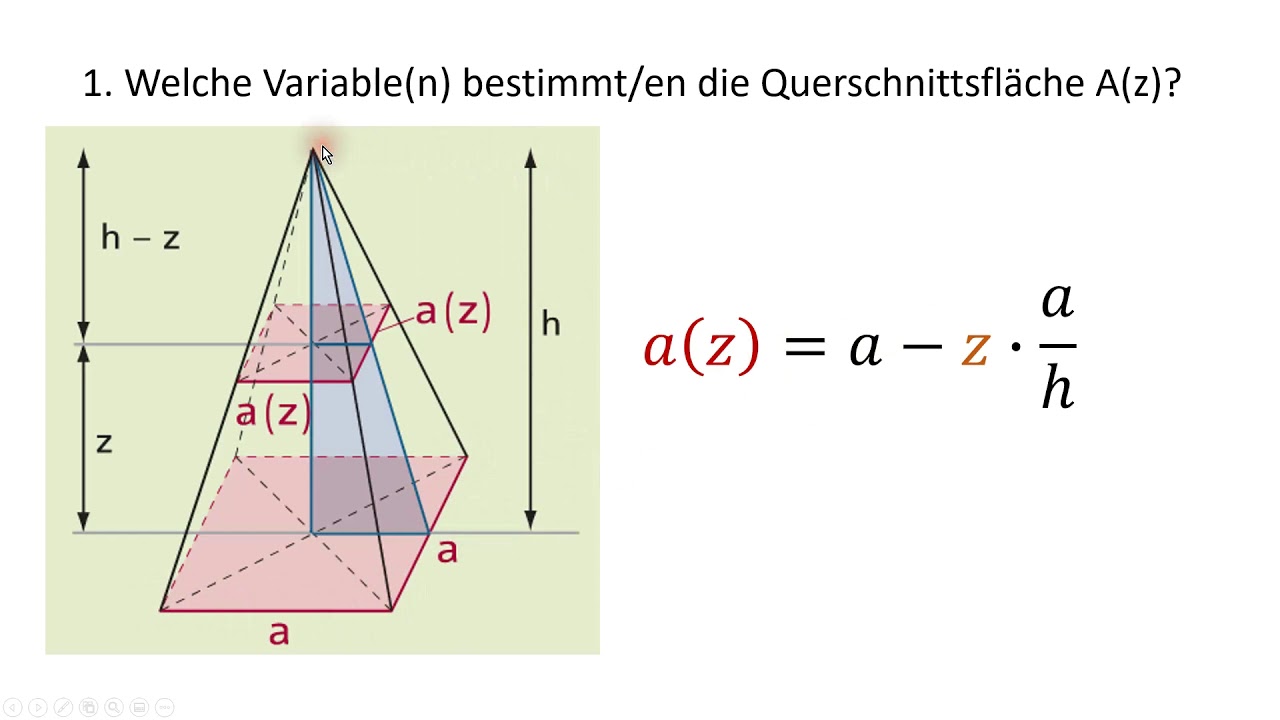
Volumsintegral quadratische Pyramide YouTube
Die Formel zur Berechnung des Volumens einer quadratischen Pyramide lautet: Volumen $=$ $\dfrac{1}{3}$ $\cdot$ Grundfläche $\cdot$ Höhe. Das ist die korrekte Formel, die Aussage ist ebenfalls wahr. Eine quadratische Pyramide hat immer $6$ dreieckige Seitenflächen. Diese Aussage sollte uns komisch vorkommen. Wir wissen schließlich, dass eine. Dieses Video wurde von Sebastian Stoll erstellt. Im Erklärvideo (Lernvideo) werden das Volumen und die Oberfläche der quadratischen Pyramide hergeleitet, erklärt und erläutert. Chapters. View.




