Aufgabe 1: Klick einen unteren Buttons an und beobachte, was passiert. Klick den nächsten Button, nachdem die grüne Umrandung des vorherigen aufgehoben wurde. Vervollständige danach unten den Satz des Pythagoras. a² + b² = c² c² - b² = a² c² - a² = b² a² + b² = c² In einem rechtwinkligen ist die der -Quadrate gleich dem Quadrat der . Auswertung Arbeitsblätter mit Übungen und Aufgaben zum Satz des Pythagoras für Mathe in der 9. Klasse am Gymnasium - mit Lösungen! Welche nützlichen Begriffe braucht man für den Satz des Pythagoras? In einem rechtwinkligen Dreieck gibt es immer eine Hypotenuse und zwei Katheten.
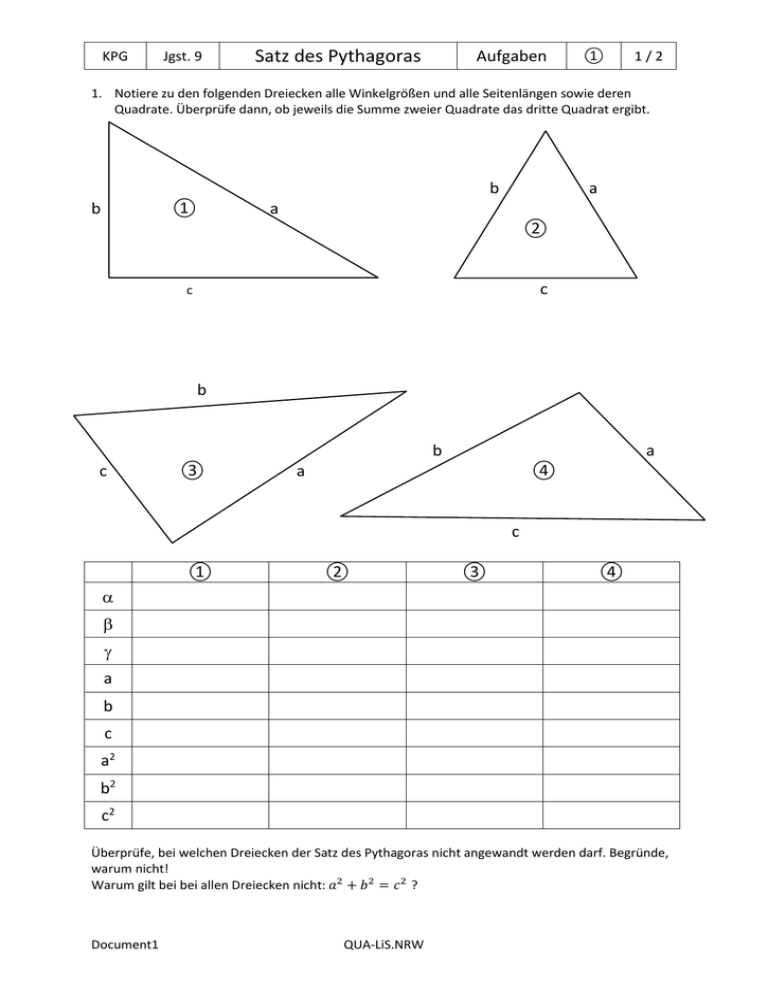
Übung zum Satz des Pythagoras
Neue Übungsblätter für Mathematik Klassenstufe 4. Übungsblatt mit Musterlösung zu Satz des Pythagoras, 5 Übungsblätter; Satz des Pythagoras. Super! Jetzt bist du fit in Übungsaufgaben und Textaufgaben zum Satz des Pythagoras! Mit dem Satz des Pythagoras kannst du nun ganz einfach fehlende Seitenlängen berechnen. Die brauchst du zum Beispiel, um herauszufinden, ob zwei Dreiecke genau aufeinander passen. 1 Gib für die rechtwinkligen Dreiecke jeweils die Gleichung nach dem Satz des Pythagoras an. Lösung anzeigen 2 Berechne bei den rechtwinkligen Dreiecken die fehlenden Seitenlängen. Lösung anzeigen 3 Berechne die Länge der Diagonalen des Rechtecks ABCD ABC D. cm Lösung anzeigen 4 Nach nebenstehender Zeichnung soll ein Doppeltor gebaut werden. Viele Anwendungen kannst du mithilfe des Satzes von Pythagoras berechnen. Zeichne zuerst immer eine Skizze. Markiere den rechten Winkel und alle gegebenen Längen. So siehst du auf den ersten Blick, welche Länge gesucht ist: eine Kathete oder die Hypotenuse. Zur Erinnerung: Der Satz des Pythagoras lautet $$c^2 = a^2 + b^2$$,
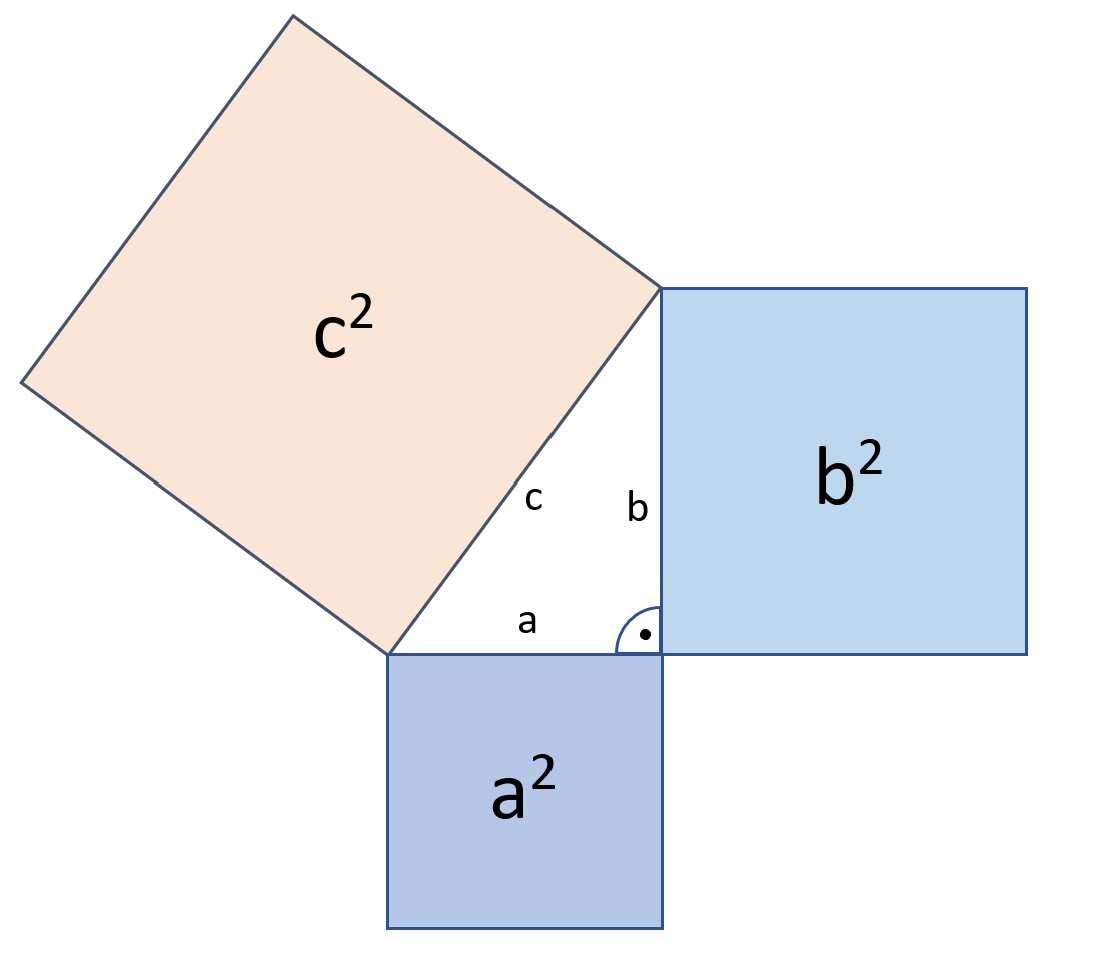
Satz des Pythagoras Die einfache SchrittfürSchrittAnleitung
Satz des Pythagoras - Umkehrung Erkennen rechtwinkliger, spitzwinkliger und stumpfwinkliger Dreiecke anhand der Seitenlängen; Anwendungen der Umkehrung des Satzes von Pythagoras Geometrie Pythagoras Verwandte Themen Geometrie Höhensatz Kathetensatz Körper Fragen und Antworten zum Thema "Pythagoras" Formuliere den Satz des Pythagoras OHNE Variablen. Zum Satz des Pythagoras in der Mathematik bekommt ihr hier einfache Übungen zum selbst Rechnen. Es geht darum die Übungen zu lösen und Fragen zum Thema zu beantworten. Löst die Übungen selbst, ohne dabei zu schummeln. Wer eine Aufgabe nicht mag, der kann auch auf "überspringen" klicken und damit zur nächsten Aufgabe springen. Satz des Pythagoras 1. Arbeitsblätter 01 Der Satz des Pythagoras 02 Aufgaben zum Satz des Pythagoras 03 Aufgaben zum Satz des Pythagoras 04 Aufgaben zum Satz des Pythagoras 05 Aufgaben zum Satz des Pythagoras 06 Aufgaben zum Satz des Pythagoras Lösungen 2. Interaktive Tests (geht nur mit Excel, wenn Makros aktiviert sind!) Satz des Pythagoras + Beweis mittels Ähnlichkeit. Kanal: Mathegym. Nach dem Satz des Pythagoras gilt in jedem rechtwinkligen Dreieck: Hypotenuse 2 = erste Kathete 2 + zweite Kathete 2. Zur Erinnerung: Die Hypotenuse ist diejenige der drei Seiten, die dem rechten Winkel gegenüber liegt. Sie ist damit auch immer die längste aller drei Seiten.
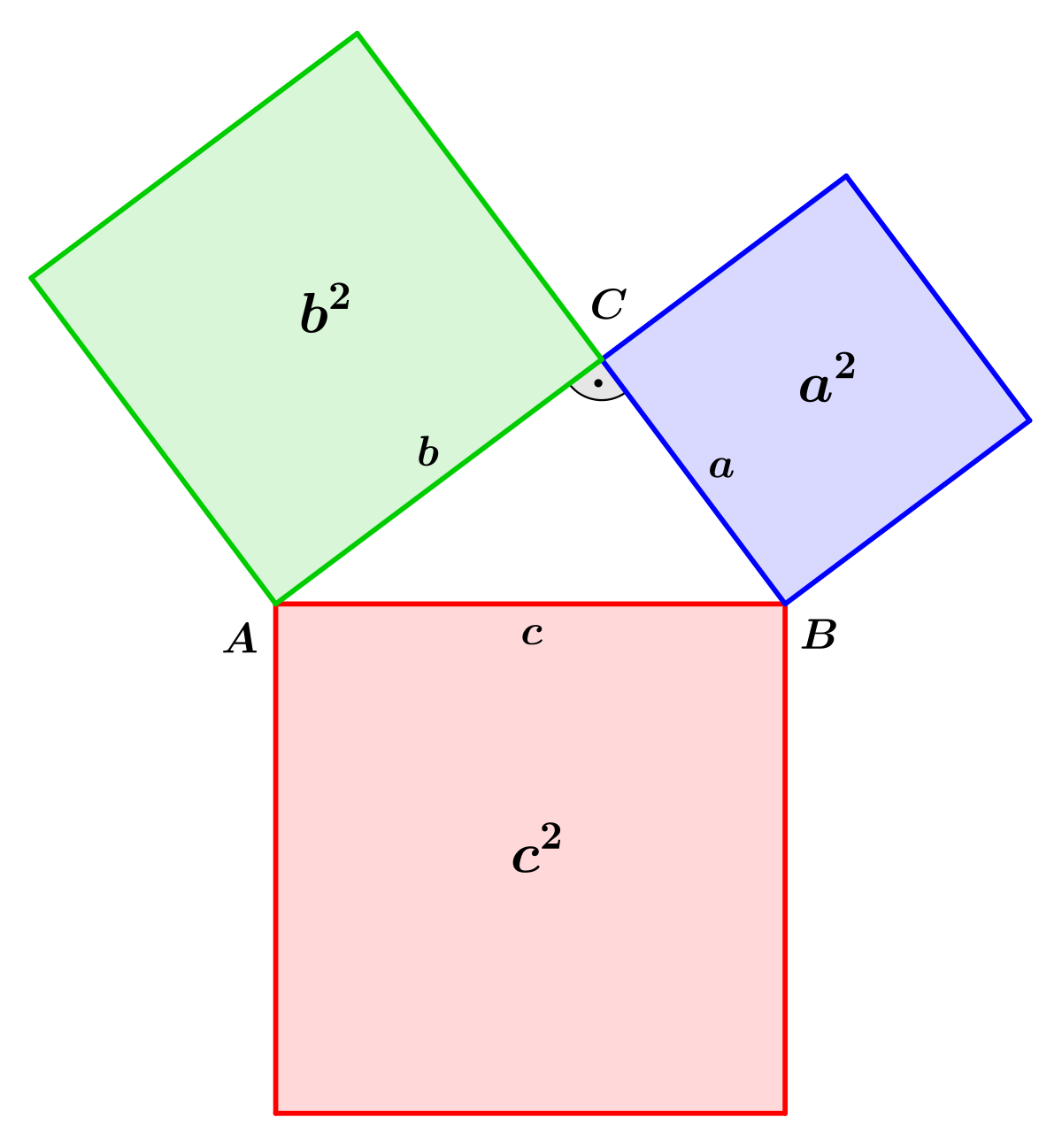
Wann zieht man bei dem Satz des Pythagoras die Wurzel? (Schule, Mathematik)
Du benötigst: Taschenrechner Steve gestaltet die Hälfte seinen Garten um in ein Hühnergehege. Sein Garten ist ein 24 mal 45 Meter großes Rechteck. Er will einen Drahtzaun setzen, der sich diagonal von einer Ecke zu der gegenüberliegenden Ecke erstreckt. Wie viele Meter Zaun braucht Steve? Meter Rechner anzeigen Steckst du fest? Hier erfährst du, wann du den Pythagoras verwenden kannst, was du dabei beachten musst und wie du Aufgaben dazu im Unterricht korrekt lösen kannst. Die Lernwege geben dir einen Überblick, welche Aufgaben und Übungen zur Satzgruppe des Pythagoras auf dich warten.
Der Satz des Pythagoras lautet aufgrund der Hypotenuse bei c so: a² + b² = c² Natürlich kannst du die Seiten der Gleichung auch umdrehen. c² = a² + b² Setze nun die Länge von a und b ein und ziehe die Wurzel, damit das ² bei c verschwindet. Kathete Kathete 0,0 Hypotenuse Abb. 1 Die Ecken des Dreiecks werden mit Großbuchstaben ( A, B, C) gegen den Uhrzeigersinn beschriftet. Die Seiten des Dreiecks werden mit Kleinbuchstaben ( a, b, c) beschriftet. Dabei liegt die Seite a gegenüber dem Eckpunkt A.
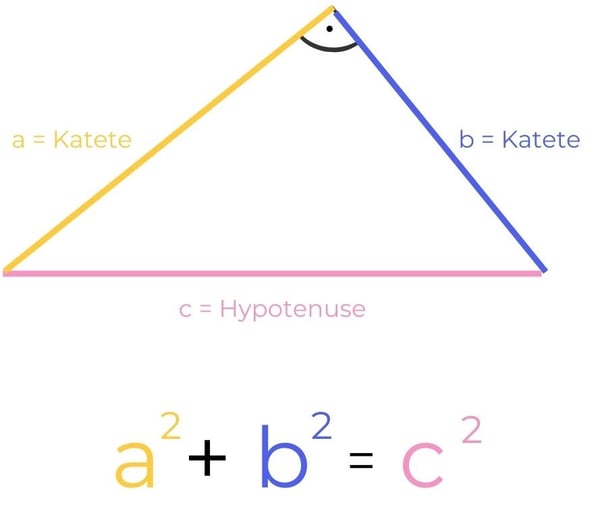
Der Satz des Pythagoras einfach erklärt Formel, Übungen & mehr
1 Der Satz des Pythagoras Stelle die richtige Gleichung für die Seiten des Dreiecks ABC ABC auf. Überprüfen Rights of use Lösung anzeigen 2 Gib für die rechtwinkligen Dreiecke jeweils die Gleichung nach dem Satz des Pythagoras an. Lösung anzeigen 3 Berechne bei den rechtwinkligen Dreiecken die fehlenden Seitenlängen. Lösung anzeigen 4 Der Satz des Pythagoras beschreibt ein spezielles Verhältnis zwischen den Seiten eines rechtwinkligen Dreiecks. Sogar in der Antike war dieses Verhältnis bekannt. In diesem Thema finden wir heraus wie der Satz des Pythagoras benutzt wird und weisen nach, warum er funktioniert.




