Satz des Thales 1 Der Satz des Thales von Milet (um 625 v.Chr — um 547 v. Chr.) besagt, dass Dreiecke, deren längste Seite der Durchmesser eines Kreises ist, genau dann rechtwinklig sind, wenn der dritte Punkt auf dem Bogen des Kreises liegt (siehe Zeichnung). Um den Satz zu beweisen, denkt man sich vom Mittelpunkt des Übungsblatt 2344. Satz des Thales, 5 Arbeitsblätter. Klassenarbeiten mit Musterlösung zum Thema Satz des Thales, Geometrie .

Arbeitsblatt Satz des Thales Mathematik tutory.de
Koordinaten des fehlenden Punktes an. a) b) Abb. 9: Planfigur des Quadrats. Abb. 10: Planfigur des Rechtecks. Aufgabe 3 In der Abbildung 8 siehst du wie die Bezeichnungen am rechtwinkligen Dreieck lauten. Aufgabe 4 Gegeben sind vier Planfiguren. Zeichne mithilfe des Thaleskreises die Vierecke. Satz des Thales - Aufgaben Seite 3 von 4 Thales - kostenloses Unterrichtsmaterial, Arbeitsblätter und Übungen. Ergebnis der Suche nach: (Freitext: THALES) Es wurden 12. Auf dieser Seite des Landesbildungsservers Baden-Württemberg wird sehr anschaulich anhand einer Animation der Satz des Thales bewiesen. Details { "HE": [] } Satz des Thales - Lernpfad. Lernpfad für das Fach. Satz des Thales (YouTube) Aufgabe 1: Stelle den Satz des Thales zusammen. Werden die von einem mit einem beliebigen auf der entsprechenden verbunden, erhält man immer ein Dreieck (90°). Aufgabe 2: Bewege in der Grafik die orangen Punkte und stelle die Winkel α aus der Tabelle im Dreieck ein. Trage die dazugehörigen Winkel β und γ in die. Ober- und Untersumme oder Riemann-Summe. Rotation oder Drehung. Vektoren 3D (dreidimensional) Trigonometrische Funktionen oder Winkelfunktionen. Statistische Kennzahlen. Satz des Thales.
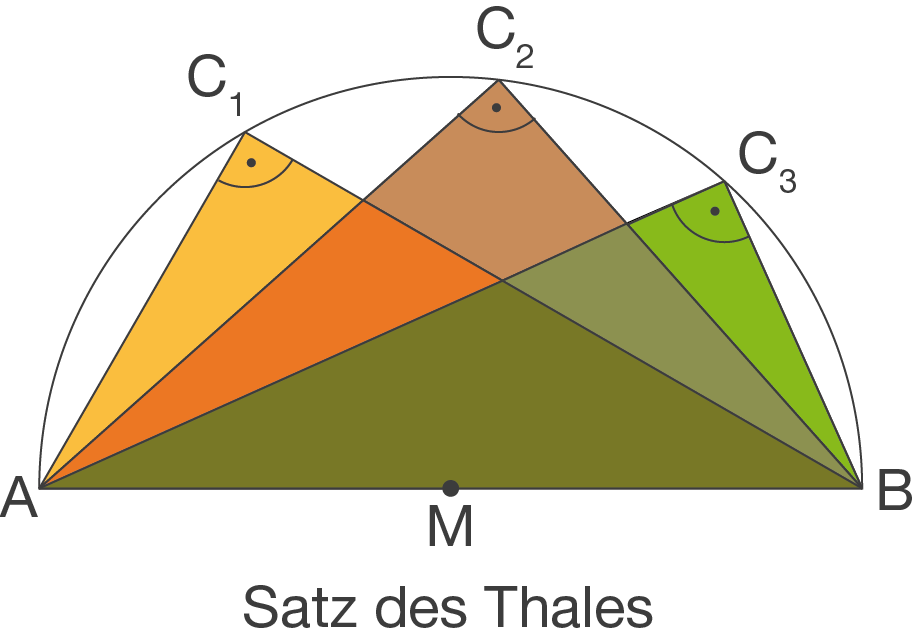
Satz des Thales SchulLV
des Beweisens wird, sondern dass Schüle-rinnen und Schüler selbstständig die Sach-verhalte rund um den Satz des Thales entde-cken und begründen können. 5.2 Satz des Thales Jahrgangsstufe 7 - 8 Die Arbeitsblätter beginnen mit einem hand-lungsorientierten Zugang auf dem Schulhof. Danach gibt es eine Folge von dynamischen Die Übungsaufgaben Satz des Thales werden in einem weiteren Beitrag gelöst, den Link dazu findet man jeweils mit einem Klick auf die Überschrift der einzelnen Aufgabe. Wir empfehlen zunächst alle Aufgaben zu rechnen, bevor man sich auf die Lösungen anschaut. Alle Rechenaufgaben zum Satz des Thales beziehen sich dabei auf folgende Zeichnung. Klasse - 8. Klasse. Best.-Nr.: VI00292. Der "Satz des Thales" besagt, dass jedes Dreieck, das aus den beiden Endpunkten des Durchmessers eines Halbkreises und einem weiteren Punkt dieses Halbkreises konstruiert wird, ein rechtwinkliges Dreieck ist. Umgekehrt gilt auch: liegen die Eckpunkte eines Dreiecks auf einem Kreis und geht die Grundseite. Arbeitsblätter für Mathematik: Thaleskreis. Der Satz des Thales besagt, dass ein Dreieck zwischen den Endpunkten eines Halbkreises und einem beliebigen Punkt auf dem Halbkreis (auch Thaleskreis genannt) immer einen rechten Winkel besitzt. Zum Thaleskreis findest du bei meinUnterricht Aufgaben mit Lösungen für verschiedene Klassenstufen.

Winkelspiel; Einführung Satz des Thales Unterrichtsmaterial im Fach Mathematik
Klassenarbeiten und Übungsblätter zu 5 Arbeitsblätter. Klassenarbeiten mit Musterlösung zum Thema 5 Arbeitsblätter, Satz des Thales. Arbeitsblatt 1 Immer im Kreis herum - Satz des Thales M 3 Platz für Skizze oder Foto Information: Satz des Thales Thales von Milet (ca. 625 v. Chr. bis 546 v. Chr.) war ein griechischer Mathematiker, Philosoph und Astronom. Er entdeckte erstmals den mathematischen Zusammenhang, der unter dem Namen „Satz des Thales" berühmt wurde.
Alles über den Satz des Thales und wie er bewiesen werden kann. Einfach erklärt in Videos und Beispielen Effektiv abgefragt mit interaktiven Übungen und Aufgaben. Arbeitsblätter zum Thema. Satz des Thales (2 Arbeitsblätter) Satz des Thales. PDF anzeigen. Satz des Thales - Anwendung. Satz des Thales. Autor: Paula Pöchtrager. Thema: Rechtwinklige Dreiecke. Schüler entdecken eigenständig den Satz desThales. Satz desThales - Arbeitsblatt 1. Satz desThales - Arbeitsblatt 2. Satz desThales - Arbeitsblatt 3. Satz des Thales - Arbeitsblatt 4. Satz des Thales - Arbeitsblatt 5. Weiter.
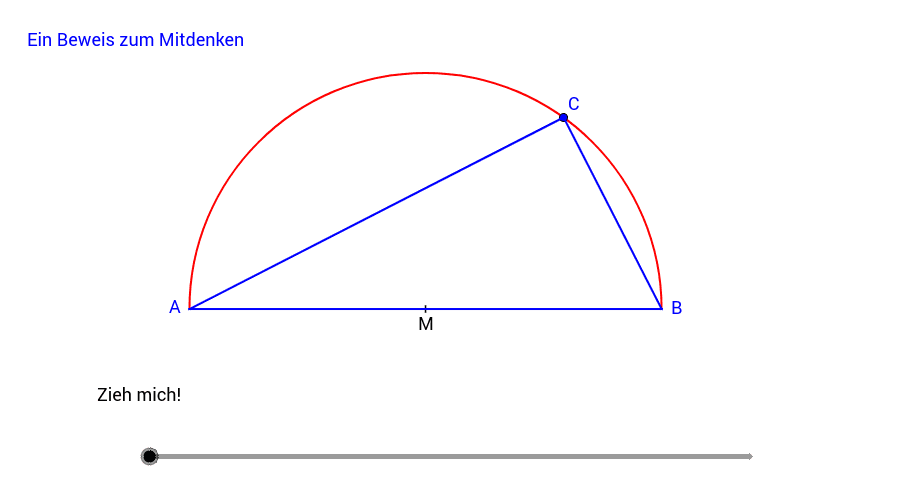
Satz des Thales Arbeitsblatt 4 GeoGebra
Satz des Thales - Arbeitsblatt. Der Satz des Thales wird formuliert und mit Hilfe von Skizzen erläutert. Dazu die Umkehrung des Satzes und der jeweilige Beweis. 1 Seite, zur Verfügung gestellt von ricksn am 16.06.2005. Der Satz des Thales besagt, dass in jedem Punkt, der auf dem Halbkreis der Strecke AB liegt, der Winkel des Dreiecks ABC 90° beträgt. Liegt C innerhalb des Dreiecks, so ist der Winkel größer als 90°.




