Wenn für die Seitenlänge der Grundfläche steht und für die Höhe der Pyramide (der senkrechte Abstand von der Grundfläche bis zur Spitze), dann kann das Volumen einer quadratischen Pyramide mit der Formel = errechnet werden. Es spielt keine Rolle, ob die Pyramide die Größe eines Briefbeschwerers hat oder größer als die Große Pyramide. Das Volumen des Quaders ist daher 3 Mal so groß wie das Volumen der Pyramide. Oder anders ausgedrückt: Das Volumen der Ppyramide ist ein Drittel des Volumens des Quaders. Somit müssen wir nur die Volumsformel des Quaders durch 3 dividieren, um die Volumsformel der Pyramide zu erhalten:
Kommandant Aktuator Mart pyramide mantel Rechnung Absay Becher
Quadratische Pyramide Oberflächeninhalt berechnen: Die Oberfläche der Pyramide liegt bei A O = 146107,2 m 2.Mit der Grundfläche und der Höhe berechnen wir das Volumen. Quadratische Pyramide Volumen berechnen: Das Volumen der Pyramide beträgt 2688000 m 3. Volumen der Pyramide berechnen. Die Formel für das Volumen der Pyramide lautet: V = 1/3 • G • h. Dabei ist G die Grundfläche und h die Höhe der Pyramide. Hast du zum Beispiel ein Quadrat mit Seitenlänge a als Grundfläche, dann rechnest du: V = 1/3 • a • a • h. Für das Volumen eines Quaders kennst du die Formel VQu = a ⋅ b ⋅ c. Also gilt: VPy = 1 3 ⋅ a ⋅ b ⋅ c. Der Term a ⋅ b ist gleich der Grundfläche G des Quaders und somit auch der der Pyramide. Der Term c ist sowohl beim Quader als auch bei der Pyramide die Höhe h. Du erhältst die Formel: VPy = 1 3 ⋅ G ⋅ h. Gilt die Formel für alle Pyramiden? Volumen V = 16 Neigung der Seitenflächen = 56,31° = 0,983 rad Neigung Seitenkante = 46,686° = 0,815 rad Seitenfläche A S = 7,211 Alle Pyramideformeln auf einen Blick Dies sind die notwendigen Formeln zum Berechnen einer quadratischen Pyramide: Link zur Grafik: https://www.matheretter.de/img/wiki/pyramide-formeln.png Was ist ein Pyramide?

Come Calcolare il Volume di una Piramide a Base Quadrata
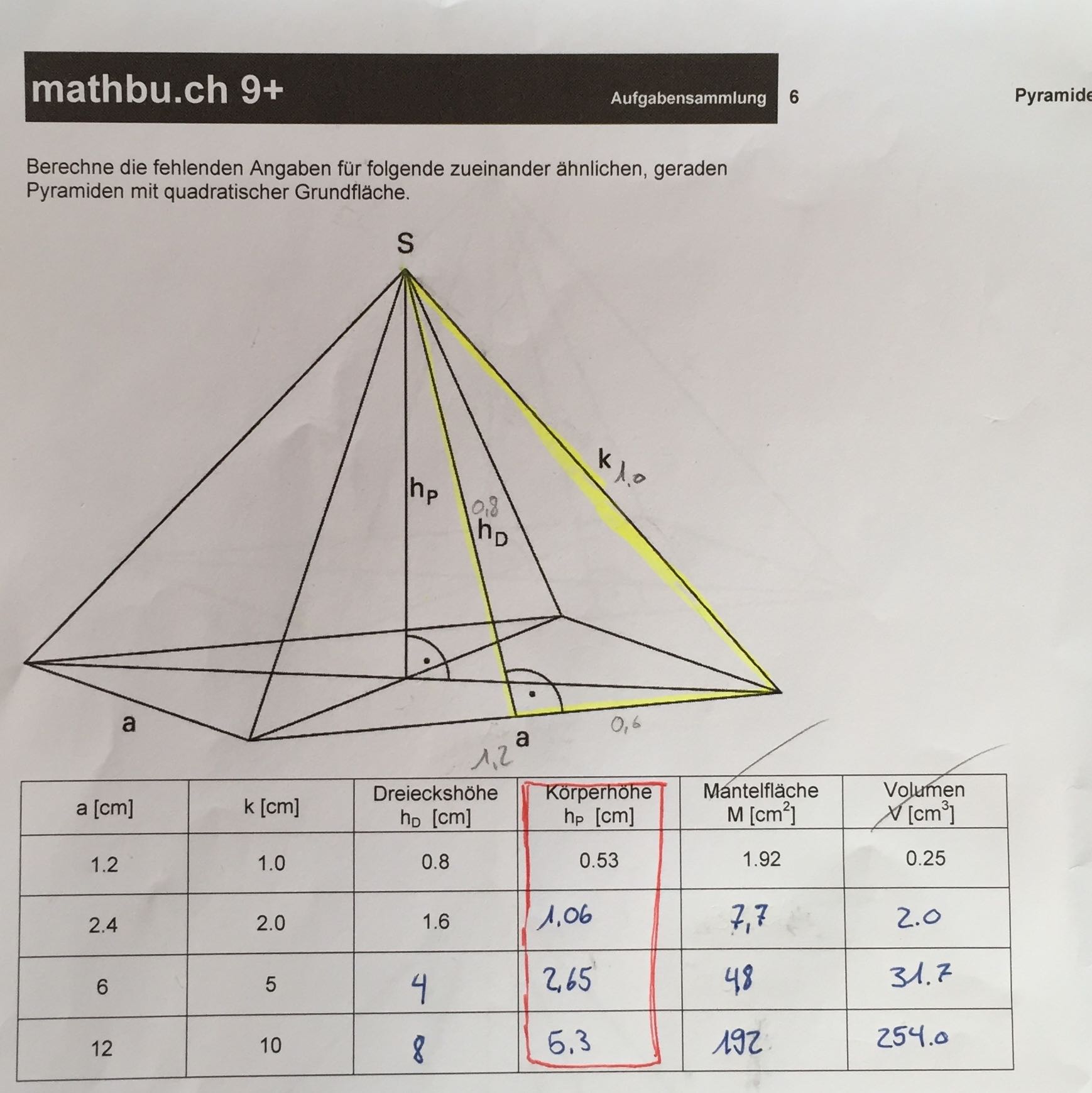
Wir berechnen das Volumen einer quadratischen Pyramide. Die quadratische Pyramide ist ein Spitzkörper. Es gilt also die Formel V = 1/3 * G * hDa die Grundflä. Berechne das Volumen der quadratischen Pyramide mit der Seitenlänge a = 3 c m und der Höhe h = 8 c m. Lösung. Um nun das Volumen berechnen zu können verwendest Du die Formel für die Berechnung des Volumens von Pyramiden und fügst als Grundfläche a 2 ein: 1.Schritt. Formel aufstellen: V = 1 3 · G · h = 1 3 · a 2 · h. 2.Schritt. Werte. Um das Volumen einer quadratischen Pyramide zu bestimmen, müssen Sie zuerst die Grundfläche der Pyramide berechnen. Dies kann durch Multiplikation der Seitenlänge des Grundquadrates erreicht werden. Anschließend können Sie die Höhe der Pyramide messen und die Formel V = 1/3 * H * A verwenden, um das Volumen zu berechnen. In diesem Video lernst Du, wie man das Volumen einer quadratischen berechnet. Außerdem zeige ich Dir, wie Du die Höhe h und die Grundkante a bestimmen kannst.
Pyramide Hohe Berechnen
Pyramide berechnen Mathepower berechnet Pyramiden problemlos. Man muß nur Grundseite und Höhe eingeben. Mathepower löst auch deine Mathe - Aufgaben. Mathematik - Hausaufgaben sind für Mathepower kein Problem. Auch die verwendeten Formeln werden angegeben. Mathepower führt Volumenberechnung durch. Show more. Dieses Video wurde von Sebastian Stoll erstellt. Im Erklärvideo (Lernvideo) werden das Volumen und die Oberfläche der quadratischen Pyramide hergeleitet, erklärt und erläutert.
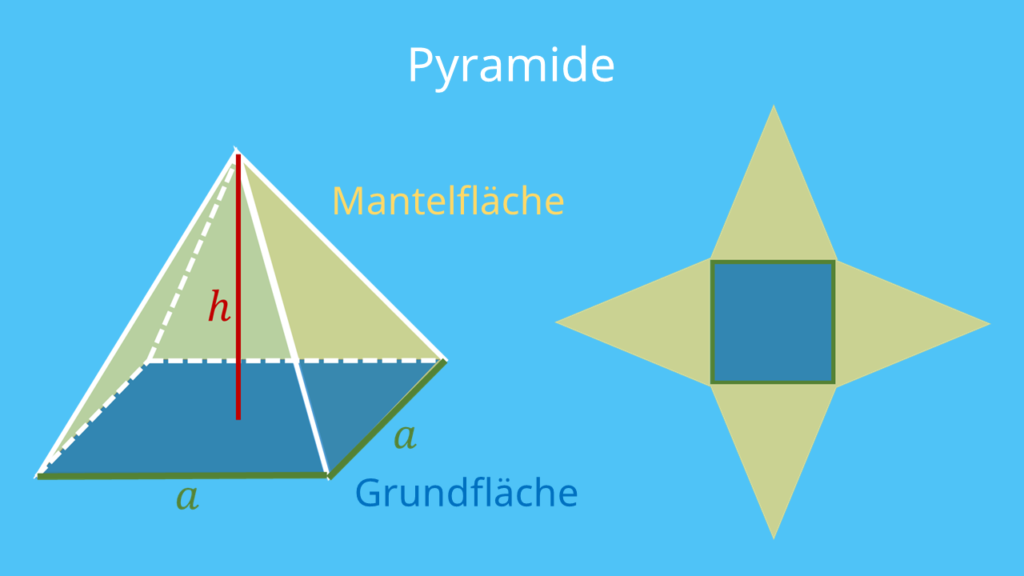
Volumen = (1/3) × Grundfläche × Höhe, wobei Höhe die Höhe von der Grundfläche bis zum Scheitelpunkt ist. Diese Formel gilt für alle Arten von Basispolygonen sowie für schräge und senkrechte Pyramiden. Alles, was du wissen musst, sind diese beiden Werte - Grundfläche und Höhe. Das Volumen (der Rauminhalt) der quadratischen Pyramide wird berechnet, indem man die Grundfläche mit der Höhe multipliziert und durch 3 dividiert. Oberfläche Die Oberfläche einer quadratischen Pyramide setzt sich aus der Grundfläche (Quadrat) und der Mantelfläche (4 kongruente gleichschenklige Dreiecke) zusammen. Formelsammlung

Volumen von Pyramide und Kegel (9. Klasse) YouTube
Unter allen quadratischen Pyramiden mit vorgegebener Oberfläche hat diejenige das größte Volumen, für die a = O 2 , h = O 2 {\displaystyle a={\frac {\sqrt {O}}{2}},\quad h={\sqrt {\frac {O}{2}}}\quad } und damit h = a ⋅ 2 {\displaystyle \quad h=a\cdot {\sqrt {2}}} Herleitung der Formel für Volumen V. Das Volumen einer Pyramide ergibt sich zu V = \frac {1} {3} 31 ·G·h. Den Faktor \frac {1} {3} 31 kann man leicht anhand eines Würfels veranschaulichen. Wir haben dabei einen Würfel mit der Kantenlänge a, also dem Volumen V W = a³. In diesen passen 6 Pyramiden, deren Spitzen sich in der Mitte treffen.




