Realschule / Gymnasium (7./8. Klasse) Winkel an sich schneidenden und an parallelen Geraden Winkelsumme im Dreieck und Viereck In den Aufgaben (und Lösungen) werden die folgenden Winkelbezeichnungen verwendet: Scheitelwinkel Nebenwinkel Innenwinkel Außenwinkel - Winkel - Winkel Arbeitsblätter mit Übungen und Aufgaben zum Thema Winkelbetrachtungen für Mathe in der 7. Klasse am Gymnasium und der Realschule - zum einfachen Herunterladen und Ausdrucken als PDF Wichtige Fachbegriffe zum Thema Winkel

Arbeitsblatt Winkel an Geradenkreuzungen Mathematik tutory.de
Winkel und Winkelsätze einfach erklärt Viele Mathematik-Themen Üben für Winkel und Winkelsätze mit interaktiven Aufgaben, Übungen & Lösungen. Übungsblatt mit Musterlösung zu Winkel, Winkelarten; Winkel zeichnen; Winkel berechnen; Aufgabensammlung aus Klassenarbeiten. Mittelsenkrechte. Thema Winkel - Kostenlose Klassenarbeiten und Übungsblätter als PDF-Datei. Kostenlos. Mit Musterlösung. Echte Prüfungsaufgaben. Ubungen zuden Winkels¨ ¨atzen - Aufgabenzum Grundwissenkatalog 1. Berechne alle eingezeichneten Winkel. o (a) (c)(b) βγ α 40o α β 60o γ δ 20 φ σ α ε γ β δ 2. Berechne α, β, γ und δ, wenn
wahlfach mathematik
Datei:Übungen Winkelsätze - Aufgaben.pdf. Größe der JPG-Vorschau dieser PDF-Datei: 424 × 600 Pixel. Weitere Auflösung: 169 × 240 Pixel. Winkelsätze für Dreiecke ----- A B αααα αααα' ββββ' ββββ γγγγ Ist p die Parallele zu AB durch C dann ist und . α' = α β' = β. Aufgaben 1. Berechne die Größe der übrigen Winkel, wenn a) und α = 27° ε = 130°. Winkelsätze und Winkelsummensatz - Übungen zum Erschließen und Anwenden. Die Arbeitsblätter M 3 (Zusatzaufgabe 1e) und M 4 (Aufgaben 2-4) werden mithilfe von GeoGebra bearbeitet. Das Programm bzw. die Dateien können mit einem QR-Code oder alternativ mit dem Link abgerufen werden. Sowohl der QR-Code als auch der Link ist auf den. Winkelsumme im Dreieck Die Summe der Winkel eines Dreiecks beträgt 180°: a + b + c = 180°. Beispiel Im Dreieck ABC werden zwei Winkel gemessen: a = 32° und b = 110°. Damit lässt sich c berechnen: 32° + 110° + c = 180° 142° + c = 180° c = 38° 6 Berechne die Winkel. 7 Berechne die Winkel b' und c' . 8 Die Geraden g und h sind parallel.

Die Schüler sollen sich mit Nebenwinkel, Scheitelwinkel, Stufenwinkel und Wechselwinkel
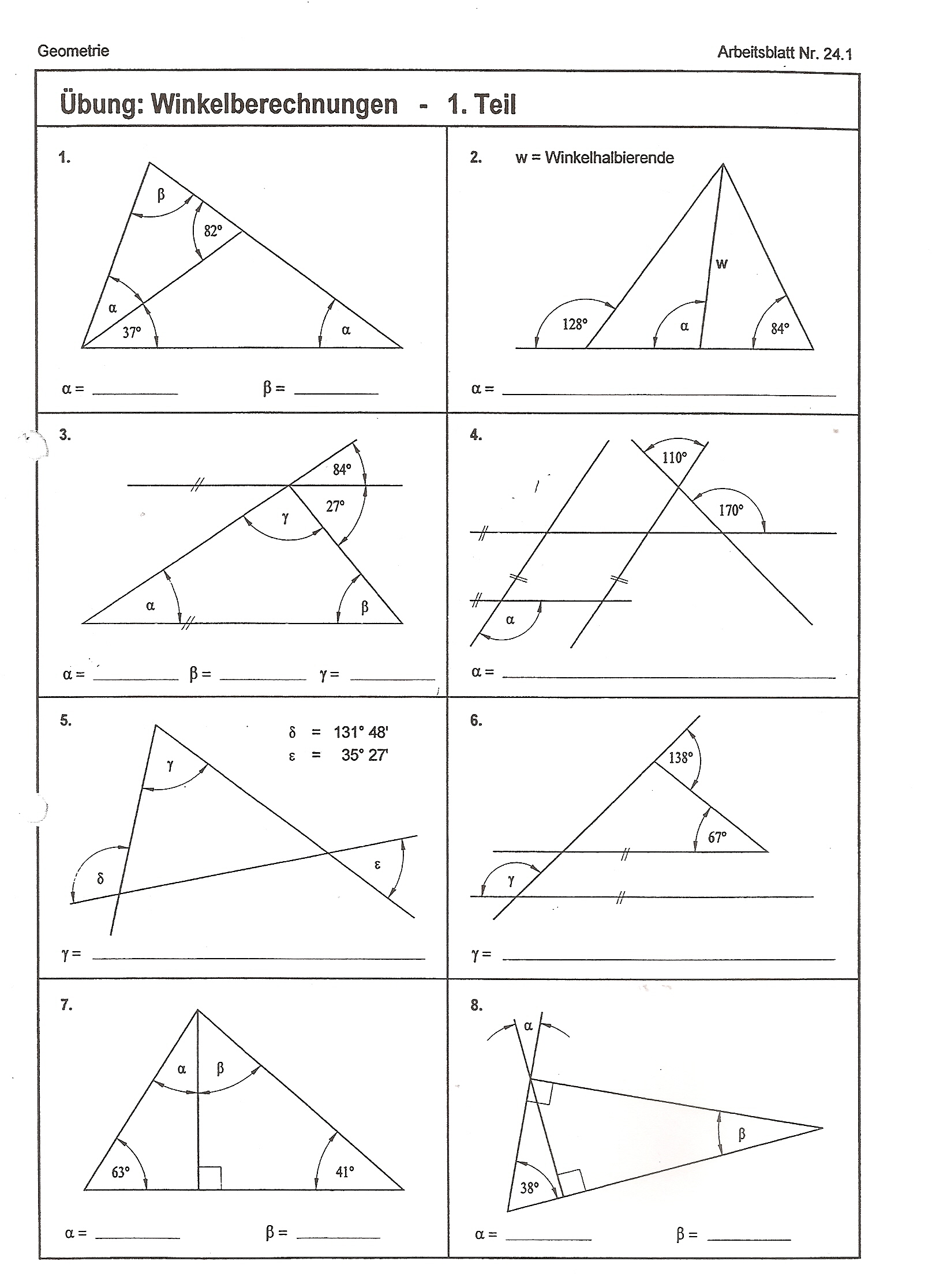
Arbeitsauftrag 1: Zeichne fünf Parallelenpaare mit unterschiedlichem Abstand. Zeichne zu jedem Paar eine Gerade, die die Parallelen unterschiedlich steil schneidet. Kennzeichne jeweils die entstandenen Winkel und messe sie. Notiere die gemessenen Größen. Vergleiche die Winkel und kennzeichne gleichgroße Winkel gleichfarbig. Winkelsätze - Beispielaufgabe . Lösung 2) .2 — — Ergebnis : 1100 Winkel berechenbar aus Satz Formel 900 (1800 - 1800 900 13 = 1800 Wert 500 400 40 70 800 30 60 1100 Aufgabe Gegeben ist die nebenstehende Figur mit 500; w ist eine Winkelhalbierende. Berechne den Winkel (3.
Dreiecke Arbeitsblatt 1 © Westermann Gruppe 1. Miss die Winkel. Addiere die Winkelgrößen. Was stellst du fest? a) = = = + + = b) c) Winkelsätze sind einfach erklärt Aussagen und Regeln über Winkel an den Schnittpunkten von mindestens zwei Geraden. Sie helfen dir beim Lösen von Aufgaben zu Winkeln in Mathe und Physik und machen dir so das Leben leichter! Winkel und Winkelsätze sind grundlegende Bestandteile der Geometrie, denen du in der Schule etwa ab der 7.

Übungsblatt zu Winkel
Halte das Geodreieck so auf der Geraden, dass die Gerade unter der langen Kante des Geodreiecks sich befindet. Suche den Wer des Restwinkels auf dem Geodreieck und markiere ihn mit einem Punkt. Verbinde nun die zwei Punkte. Zeichne den gesamten überstumpfen Winkelbogen ein und schreibe den Winkelwert auf. 1) Innenwinkelsatz. Die Summe der Innenwinkel in einem n-Eck ist (n-2)·180°. Beispiel: Die Summe der Innenwinkel in einem Dreieck (n = 3) beträgt (3-2)·180° = 180°. 3) Neben dem Innenwinkelsatz gibt es noch den Stufenwinkelsatz und den Wechselwinkelsatz. Der Wechselwirkungssatz lautet: wenn zwei Geraden parallel sind, dann sind.




