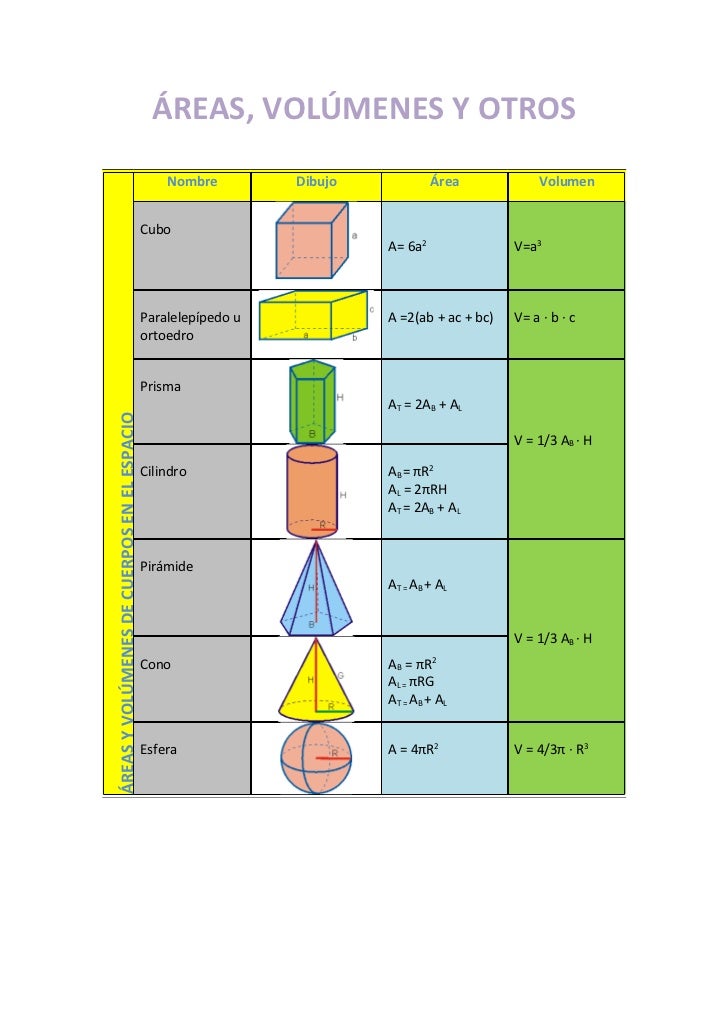
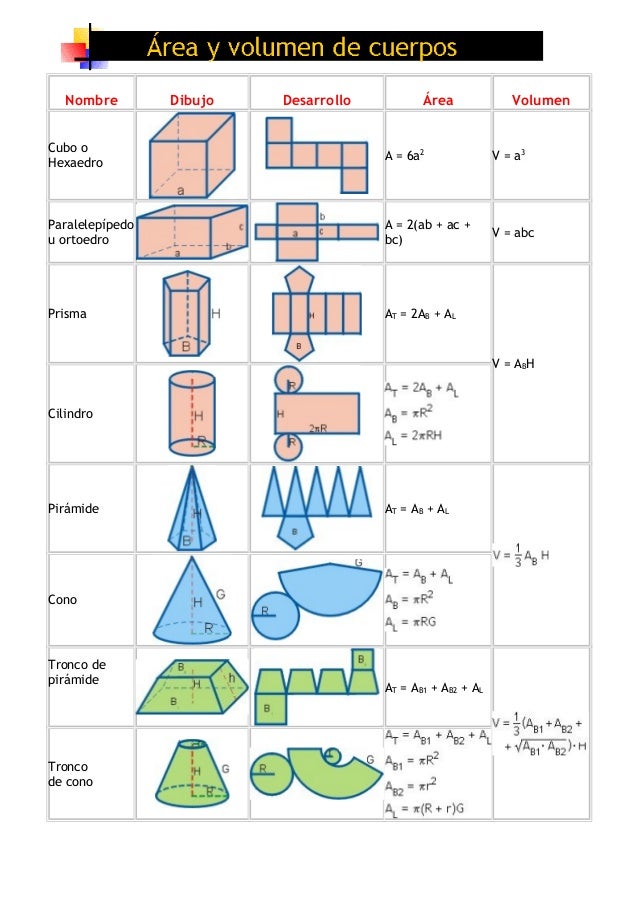
PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS CUERPOS ESFÉRICOS es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los principales elementos de un poliedro son: Caras o polígonos que lo limitan. Aristas o lados de las caras. Vértices o puntos de corte de las aristas. Diagonales o segmentos dos vértices de distintas caras. Fórmulas de área y volumen de cuerpos geométricos Fórmula de Euler: C + V - A = 2 donde, C= no de caras, V= no de vértices, A= no de aristas EJERCICIOS DE VOLÚME ES Ejercicio no 1.- Expresa en cm3: 1 m3 5 400 mm3 0,003 dam3 Solución: 1 m3 = 1 · 1 000 000 cm3 = 1 000 000 cm3 5 400 mm3 = 5 400 : 1 000 cm3 = 5,4 cm3
Tema 8 areas y volúmenes
Descarga el formulario de geometría Dale clic al siguiente botón para bajar el formulario: Formulario de geometría En este documento, encontrarás las fórmulas de áreas y volúmenes de las siguientes figuras: Triángulo. Cuadrado. Rectángulo. Trapecio. Paralelogramo. Circunferencia. Elipse. Cubo. Esfera. Cilindro. Cono. Tronco de cono. El área es el espacio de dos dimensiones que ocupa una figura, en cambio, el volumen es el espacio de tres dimensiones que ocupa un cuerpo geométrico. Por ejemplo, una viga redonda en posición vertical es un cilindro que tiene un gran volumen porque es un objeto muy alto. 9.5: Área y Volumen de Figuras Geométricas y Objetos Page ID Denny Burzynski & Wade Ellis, Jr. College of Southern Nevada via OpenStax CNX Objetivos de aprendizaje conocer el significado y la notación para el área conocer las fórmulas de área para algunas figuras geométricas comunes Área, perímetro y volumen de figuras del plano y del espacio www.vaxasoftware.com A = Área, S = Área, P = Perímetro, V = Volumen Figuras del plano Cuadrado A a2 Ángulo interno 90 P 4a Ángulo externo 90 Núm. diagonales ND 2 Rectángulo A b·h P 2b 2h Paralelogramo A b·h P 2b 2a c2 d2 2(a2 b2)
Cálculo deáreasyvolúmenes
TEORÍA Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos geométricos. A lo largo de todos los tiempos se han utilizado estos cuerpos en el arte y en la arquitectura. Áreas, Perímetros y Volúmenes de Figuras Geométricas Prontuario con las expresiones y fórmulas para el cálculo de áreas, perímetros y volúmenes de figuras geométricas. >> FIN DEL CONTENIDO Programa de Colaboración Ahora puedes colaborar en el sostenimiento de esta web realizando un pequeño donativo Gracias por tu colaboración Comenzaremos con el volumen y el área de prismas rectangulares. Desde ahí, abordaremos objetos más complicados, como conos y esferas.. Áreas superficiales usando desarrollos; Área de la superficie;. Descomposición de figuras para calcular su volumen ¡Obtén 3 de 4 preguntas para subir de nivel! Volumen con fracciones. 3. Si no queremos memorizar las fórmulas para hallar el volumen de los troncos, lo que se hace es utilizar la. semejanza de triángulos y el teorema de Tales. Para hallar el área y el volumen de un huso esférico podemos usar una regla de tres simple directa. Otras fórmulas: Fórmula de Herón. para calcular el área de un. triángulo:

Formulas volumen figuras geométricas
SOLUCIONES. 4 cm + 5 cm + 8 cm = 17 cm. El largo es el triple del ancho, es decir se multiplica el ancho por 3. El largo mide 3 3, o sea 9. Perímetro: dos veces el largo más dos veces el ancho. 2 9 = 18. 2 3 = 6. Sumando: 18 + 6 =24. Respuesta: el perímetro del rectángulo ilustrado es de 24 m. DEF. Un cuerpo de revolución es un cuerpo geométrico que se obtiene a partir de una figura plana que gira alrededor de un lado CILINDRO: es un cuerpo geométrico generado a partir de un rectángulo que gira alrededor de uno de sus lados. Área: A = Alateral + 2·Abase A = 2 r h + 2 r2 Volumen: V = Abase ∙ h V = r2 h CONO:
A continuación se muestran las fórmulas de todas las áreas de figuras planas. De manera que podrás ver las fórmulas de las áreas de polígonos regulares, de figuras circulares y, en definitiva, de cualquier figura plana regular. Área de un triángulo. El área de un triángulo es igual a la base del triángulo por su altura partido por. 1 Calcula el volumen, en centímetros cúbicos, de una habitación que tiene m de largo, m de ancho y m de alto. Solución. 2 Una piscina tiene m de largo, m de ancho y m de profundidad. Se pinta la piscina a razón de € el metro cuadrado. A Cuánto costará pintarla. B Cuántos litros de agua serán necesarios para llenarla.

AREAS Y VOLUMENES DE CUERPOS GEOMETRICOS PDF
Áreas y Volúmenes de Figuras en el espacio Cubo Ortoedro Circunferencia 62 A a Lat V a 3 2 · · · A ab bc acLat V abc ·· 24·· A r Lat 4··3 3 V r Cilindro Cono Pirámide A rhLat 2··· ·· 2 2 A rg g h r Lat · 2 Base c Lat Perímetro h A Fórmulas de áreas de cuerpos geométricos. A continuación se muestran las fórmulas de las áreas de cuerpos geométricos, es decir, de los cuerpos que ocupan un espacio tridimensional y, por tanto, tienen un volumen. Área de un cubo. El área de un cubo se calcula sumando las áreas de sus seis caras cuadradas. Por lo tanto, el área de un.




