Barns and boxes Decorative items Properties of a Pentagonal Prism A pentagonal prism consists of various properties that are unique to this solid shape. Listed below are some of the properties of a pentagonal prism: A pentagonal prism has 15 edges, 7 faces, and 10 vertices. The base of a pentagonal prism is in the shape of a pentagon. Math Article Pentagonal Prism Pentagonal Prism A pentagonal prism is a prism that has two pentagonal bases like top and bottom and five rectangular sides. It is a type of heptahedron with 7 faces, 10 vertices and 15 edges. A pentagonal prism can have pentagonal bases which give five sides.
Prisma Pentagonal Características Volumen y Área
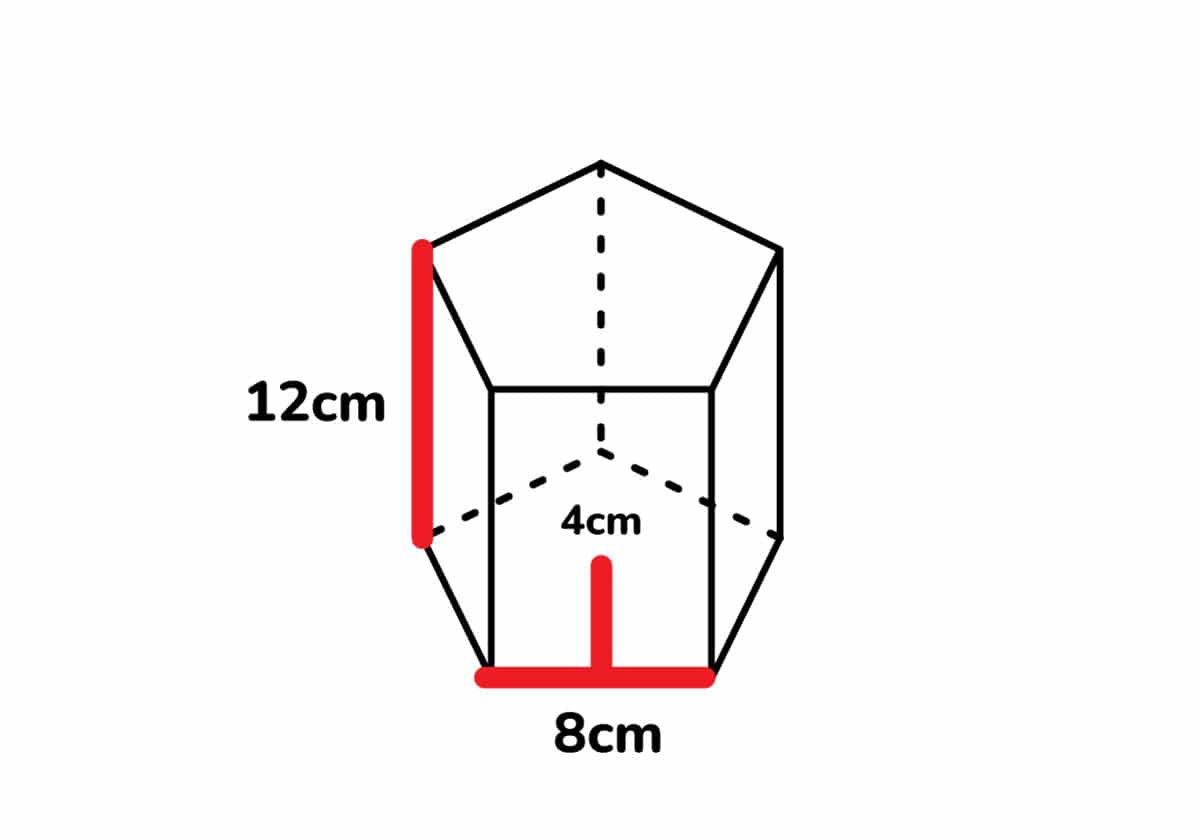
A pentagonal prism is a type of heptahedron having 7 faces, 15 edges, and 10 vertices. It is a 3-D shape that has a pentagon base and a pentagon top. Like all three-dimensional shapes, you will learn how to calculate the surface area of a pentagonal prism. Let's learn more about its formula using solved examples. The dual of a pentagonal prism is a pentagonal bipyramid. The symmetry group of a right pentagonal prism is D 5h of order 20. The rotation group is D 5 of order 10. Volume. The volume, as for all prisms, is the product of the area of the pentagonal base times the height or distance along any edge perpendicular to the base. Total Surface Area of a Pentagonal Prism A regular pentagonal prism's total surface area gives each face's area (i.e., seven prism faces). Thus, the total surface area of the regular pentagonal prism is calculated as: TSA = 5 a b + 5 b h square units. We can find the volume of a pentagonal prism by multiplying the area of the base by the height of the prism. Recall that we can use the apothem to calculate the area of polygons easily. Therefore, we have the following formula: V = \frac {5} {2} alh V = 25alh. where a represents the length of the apothem, l represents the length of the sides of.

Pentagonal Prism Cuemath
The surface area (or total surface area) of a pentagonal prism is the entire amount of space occupied by all its outer surfaces (or faces). It is measured in square units such as m 2, cm 2, mm 2, and in 2. Formula. The formula is given below: Surface Area of a Pentagonal Prism. The formula for a pentagonal prism is {eq}Surface Area = 5ab + 5bh {/eq} where "a" is the apothem of the pentagon, "b" is the base of the pentagon, and "h" is the height of the prism. Example: What is the volume of a prism where the base area is 25 m 2 and which is 12 m long: Volume = Area × Length. = 25 m2 × 12 m. = 300 m3. Play with it here. The formula also works when it "leans over" ( oblique) but remember that the height is at right angles to the base: And this is why: The pentagonal prism is a prism having two pentagonal bases and five rectangular sides. It is a heptahedron. The regular right pentagonal prism is uniform polyhedron U_(76). Its dual polyhedron is the pentagonal dipyramid. A (possibly nonregular) pentagonal prism is the convex hull of the pentagrammic antiprism, pentagrammic prism, and pentagrammic crossed antiprism.
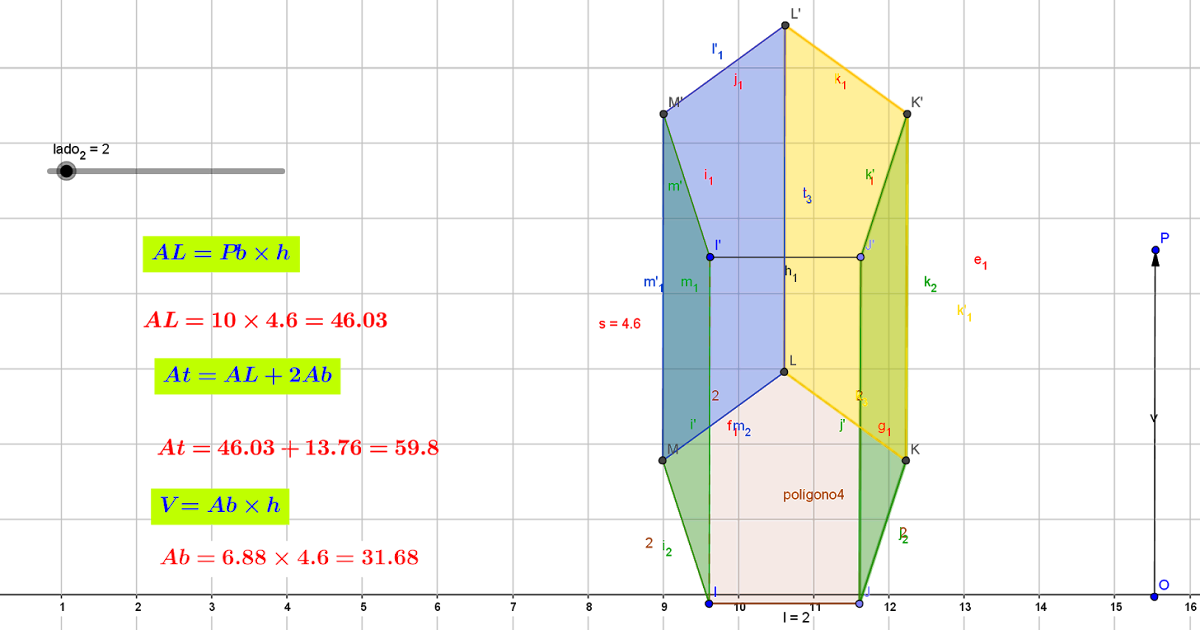
LA VENTANA DE LA MATEMÁTICA ÁREA Y VOLUMEN DE UN PRISMA PENTAGONAL
Así pues, el área de un prisma pentagonal regular es igual a cinco por el lado del pentágono por la suma de la apotema más la altura. De modo que la fórmula del área de un prisma pentagonal regular es la siguiente: Puedes usar la calculadora que hay más abajo para calcular el área de cualquier prisma pentagonal regular. The surface area of a pentagonal prism can be calculated using the formula: A = 2 × B + P × h, where B is the area of the base, P is the base's perimeter, and h is the height of the prism. The term 2B gives the combined area of the bases, and Ph gives the total area of the rectangular faces.
Pentagonal Prism. Hexagonal Prism. The formula for determining the surface area of a pentagonal prism is defined as: S A = 5 ⋅ a ⋅ h + 5 ⋅ ( 5 + 2 ⋅ 5) 2 ⋅ a 2. S A: the surface area of the prism. a: the length of any side of the bases. h: the height of the prism. The SI unit of surface area is: s q u a r e m e t e r ( m 2) A pentagonal prism is a prism with the base of a pentagon. They can be regular, irregular, right or oblique but they each contain 7 faces, 15 edges, and 10 vertices.

cual es el área total de el prisma pentagonal Brainly.lat
Base area of a pentagonal prism $= \frac{1}{2} \times P \times a$ $= \frac{1}{2} \times 25 \times 3.4$ $= 42.5$ square units. Hence, the base area of a pentagonal prism $= 42.5$ square units. 5. Find the height of the pentagonal prism if the apothem length is 4 inches, the base length is 6 inches and its volume is 540 cubic inches. Solution: How To Calculate The Pentagonal Prism Surface Area Your Self. Calculating the surface area is rather simple when you know the formula presented above. Follow these steps: Write down this formula: P: = 5 ⋅ e ⋅ h + 1 2 ⋅ 5 ⋅ ( 5 + 2 ⋅ 5) ⋅ e 2.




