ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. To-dos estos objetos son cuerpos geométricos. A lo largo de todos los tiempos se han utilizado estos cuerpos en el arte y en la arquitectura. Fórmulas de área y volumen de cuerpos geométricos Fórmula de Euler: C + V - A = 2 donde, C= no de caras, V= no de vértices, A= no de aristas EJERCICIOS DE VOLÚME ES Ejercicio no 1.- Expresa en cm3: 1 m3 5 400 mm3 0,003 dam3 Solución: 1 m3 = 1 · 1 000 000 cm3 = 1 000 000 cm3 5 400 mm3 = 5 400 : 1 000 cm3 = 5,4 cm3

Fórmulas de área y volumen de cuerpos geométricos
Cuerpos geométricos En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos geométricos. A lo largo de todos los tiempos se han utilizado estos cuerpos en el arte y en la arquitectura. Áreas y Volúmenes ¡Bienvenid@ a areasyvolumenes.net! Aquí encontrarás toda la teoría relacionada con perímetros, áreas y volúmenes de figuras geométricas, ejemplos resueltos paso a paso y calculadoras para que puedas calcular el perímetro, el área o el volumen de cualquier cuerpo geométrico directamente. 9.5: Área y Volumen de Figuras Geométricas y Objetos Page ID Denny Burzynski & Wade Ellis, Jr. College of Southern Nevada via OpenStax CNX Objetivos de aprendizaje conocer el significado y la notación para el área conocer las fórmulas de área para algunas figuras geométricas comunes DEF. Un poliedro (muchas caras) es un cuerpo geométrico en el espacio limitado por cuatro o más caras (polígonos) que encierran un volumen. PRISMA: es un poliedro que tiene dos caras iguales paralelas entre sí, bases, y las restantes caras son paralelogramos. PRISMA RECTO Área: A = Alateral + 2·Abase Volumen: V = Abase ∙ h
Fórmulas De área Y Volumen De Cuerpos Geométricos
Áreas y volúmenes de cuerpos geométricos. Cómo calcular el área y el volumen de pirámides, conos y diversos prismas, explicado todo paso a paso.Área y volume. En este directo aprenderemos a calcular ÁREAS y VOLÚMENES de CUERPOS GEOMÉTRICOS COMPUESTOS 👌😉SERIE sobre GEOMETRÍA 👉 https://www.youtube.com/playlist?li. 10 Volumen de los cuerpos geométricos. Objetivos En esta quincena aprenderás a: Comprender el concepto de "medida del volumen" y conocer manejar las unidades de medida del S.M.D. Obtener y aplicar expresiones para el cálculo de volúmenes de cuerpos geométricos comunes. Observar las posibles similitudes entre algunas de dichas expresiones. 9 Objetivos En esta quincena aprenderás a: Calcular el área de prismas rectos de cualquier número de caras. Calcular el área de pirámides de cualquier número de caras. Calcular el área de un tronco de pirámide. Calcular el área de un cilindro. Calcular el área de un cono. Calcular el área de un tronco de cono. Calcular el área de una esfera.

Ejercicios de Repaso
Poliedros: son los cuerpos geométricos que están formados por caras planas (polígonos) y tienen volumen porque encierran un espacio.; Cuerpos redondos o cuerpos de revolución: son la esfera, el cono y el cilindro.Se llaman así porque se pueden conseguir haciendo girar una figura sobre un eje. Antes de conocer qué son los poliedros, vamos a ver las diferencias que existen entre éstos y. A continuación se muestran las fórmulas de las áreas de cuerpos geométricos, es decir, de los cuerpos que ocupan un espacio tridimensional y, por tanto, tienen un volumen. Área de un cubo El área de un cubo se calcula sumando las áreas de sus seis caras cuadradas.
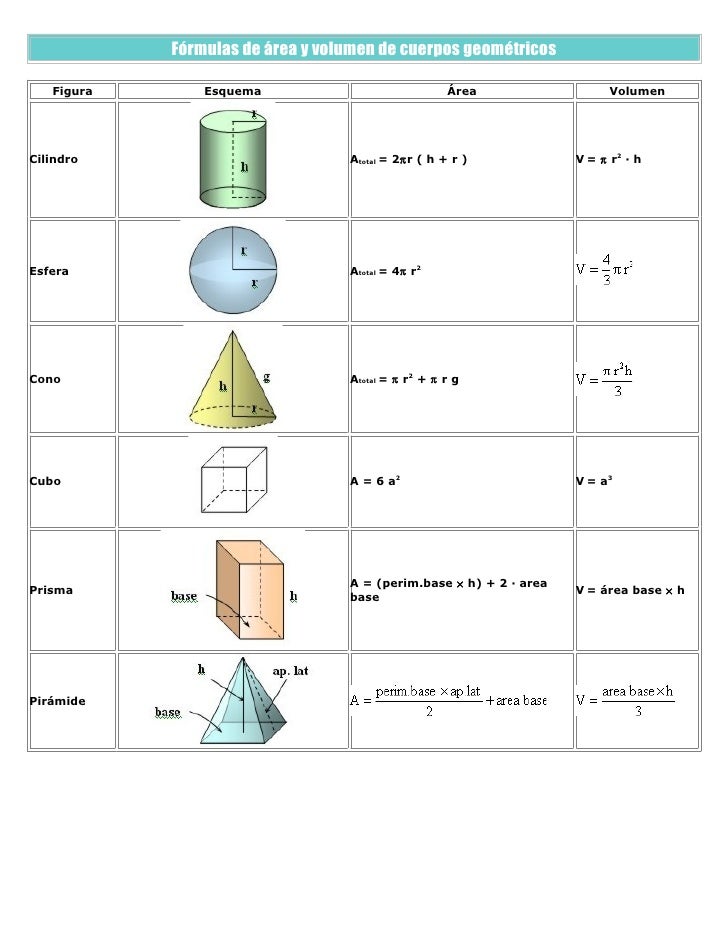
Fórmulas de área y volumen de cuerpos geométricos Daiana Pinget Cilindro Atotal = 2π r (h + r) V = π r 2 · h Esfera Atotal = 4π r 2 Cono Atotal = π r 2 + π r g Cubo A = 6 a 2 V = a 3 Prisma A = (perim.base × h) + 2 · area base V = área base × h Pirámide See Full PDF Download PDF Related Papers El volumen total de cuerpos geométricos, como el ortoedro y el cubo , se halla multiplicando sus tres dimensiones: largo, ancho y alto. De igual manera, el volumen del cilindro y la pirámide se halla multiplicando el área de las bases por su altura. 1. Comprender el concepto de volumen de los cuerpos. 2. Relacionar las unidades de volumen.

Areas Y Volumenes De Figuras Geometricas Figuras Images
d) 0,5 cm3. 18. Expresa en centímetros cúbicos estas cantidades: a) 250 cL b) 2,5 L. c) 6500 mL. 19. Calcula el volumen de un prisma hexagonal regular, siendo el lado de su base 8 centímetros, la apotema 7 centímetros, y la altura del prisma 20 centímetros. 20 Calcula el volumen del prisma de la figura. 1 Calcula el volumen, en centímetros cúbicos, de una habitación que tiene m de largo, m de ancho y m de alto. Solución. 2 Una piscina tiene m de largo, m de ancho y m de profundidad. Se pinta la piscina a razón de € el metro cuadrado. A Cuánto costará pintarla. B Cuántos litros de agua serán necesarios para llenarla.




