- Derivada de la función exponencial de base "e" - Si la base de la función exponencial es el número "e" su derivada es igual a la derivada del exponente por el número elevado al exponente. Ejemplo: También podemos resolverlo aplicando las propiedades de los logaritmos: Obtenemos el mi Calculadora gratuita de derivadas - Solucionador de derivadas paso por paso

Fórmulas de Derivadas Derivadas
La derivada de la función exponencial de base e es igual a la misma función por la derivada del exponente. Derivada de e a la x. Para el caso especial. Tenemos que. Siguiendo la fórmula anterior. Se concluye que. Y así, decimos que la derivada de es . Ejercicios de derivadas propuestos. 1 . Ejemplos de la forma de encontrar la derivada de la función exponencial, derivada de e^x, dentro del curso de derivadas.Curso completo de Derivadas:https://w. Free Pre-Algebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step La derivada de una función describe la razón de cambio instantáneo de la función en un cierto punto. Otra interpretación común es que la derivada nos da la pendiente de la recta tangente a la gráfica de la función en ese punto. Aprende cómo definimos la derivada mediante límites. Conoce un conjunto de reglas muy útiles (como las reglas de potencia, producto y cociente) que nos.
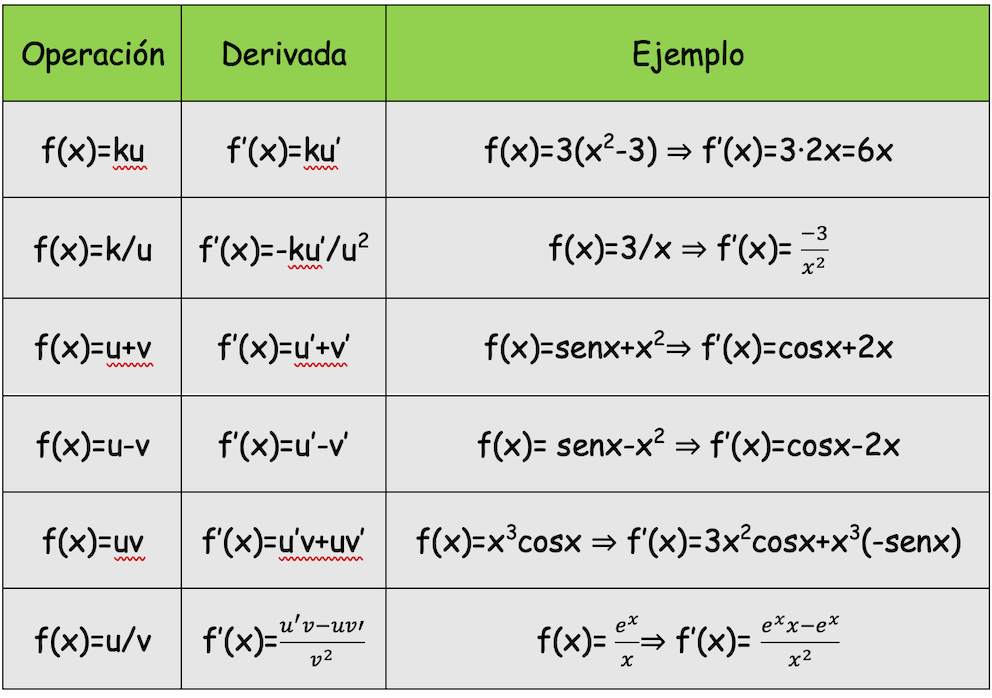
las 7 】propiedades de las derivadas
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history. ¿Cómo derivo funciones exponenciales? Primero debes conocer las derivadas de las funciones exponenciales básicas: d d x ( e x) = e x d d x ( a x) = ln ( a) ⋅ a x Observa que e x es un caso específico de la forma general a x donde a = e . Como ln ( e) = 1 obtenemos el mismo resultado. La derivada como concepto Rectas secantes y razones de cambio promedio Repaso sobre la notación para la derivada La derivada como la pendiente de una curva La derivada y las ecuaciones de la recta tangente La pendiente de una recta secante a una curva Recta secante con diferencia arbitraria Recta secante con punto arbitrario Para hacer la derivada de la función exponencial de base e hay que multiplicar la función sin derivar por la derivada de su exponente. Se trata de una fórmula simple de fácil aplicación: SOLUCIÓN y fórmula de la derivada de una función exponencial de base e f (x)= e^u f (x) = eu f' (x)=u'\cdot e^u f ′(x) = u′ ⋅ eu

Resultado de imagen para tabla de derivadas e integrales Basic math, Math formulas, Math geometry
Derivadas Aplicaciones de la derivada Limites Integrales Aplicaciones de la integral Aproximación integral Series EDO Cálculo multivariable Transformada de Laplace Serie de Taylor/Maclaurin Serie de Fourier. Funciones. Ecuaciones de la recta Funciones Aritmética y composición Secciones cónicas Transformación. Wolfram|Alpha calls Wolfram Languages's D function, which uses a table of identities much larger than one would find in a standard calculus textbook. It uses well-known rules such as the linearity of the derivative, product rule, power rule, chain rule and so on. Additionally, D uses lesser-known rules to calculate the derivative of a wide.
Te explico 6 derivadas de expresiones que contiene a Euler.SEGUNDA PARTE: https://youtu.be/sNHibbsolbAAdemás, recuerda compartir el vídeo con tus compañeros. Dada una función , hay varias formas de denotar la derivada de con respecto a . Las formas más comunes son y . Cuando una derivada se toma veces, la notación o es utilizada. Estas son llamadas derivadas de orden superior. Note que por derivadas de segundo orden, la notación es usualmente utilizada. En un punto , la derivada se define como .

Tabla de derivadas
La derivada de e, ya que es una constante, es igual a cero. De igual modo sucede con la derivada de e elevado a cualquier número natural n (en). Ahora, puede ser que e esté elevado a una función. En este caso, la derivada de esa función exponencial será igual a la derivada del exponente por la función original. La derivada de una función lineal es el coeficiente del término de primer grado, es decir, la derivada de una función lineal f (x)=Ax+B es igual a A Fíjate en los siguientes ejemplos cómo se han derivado este tipo de funciones: Derivada de una potencia




