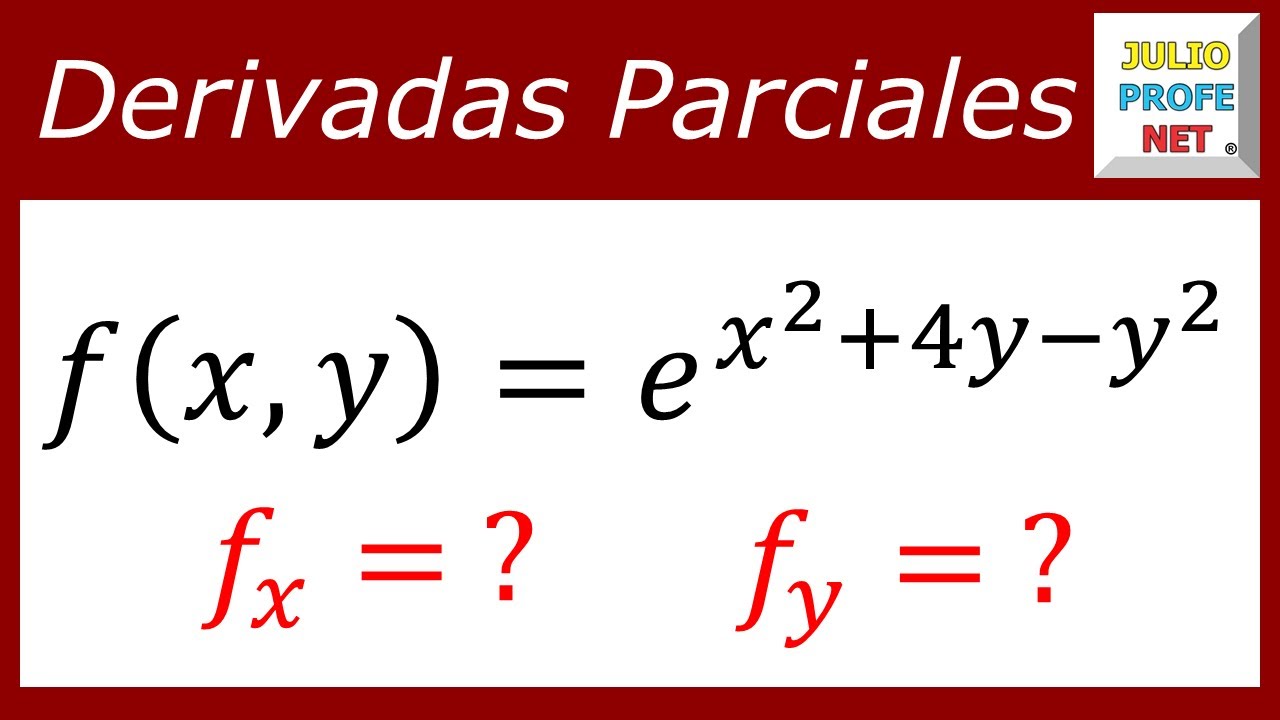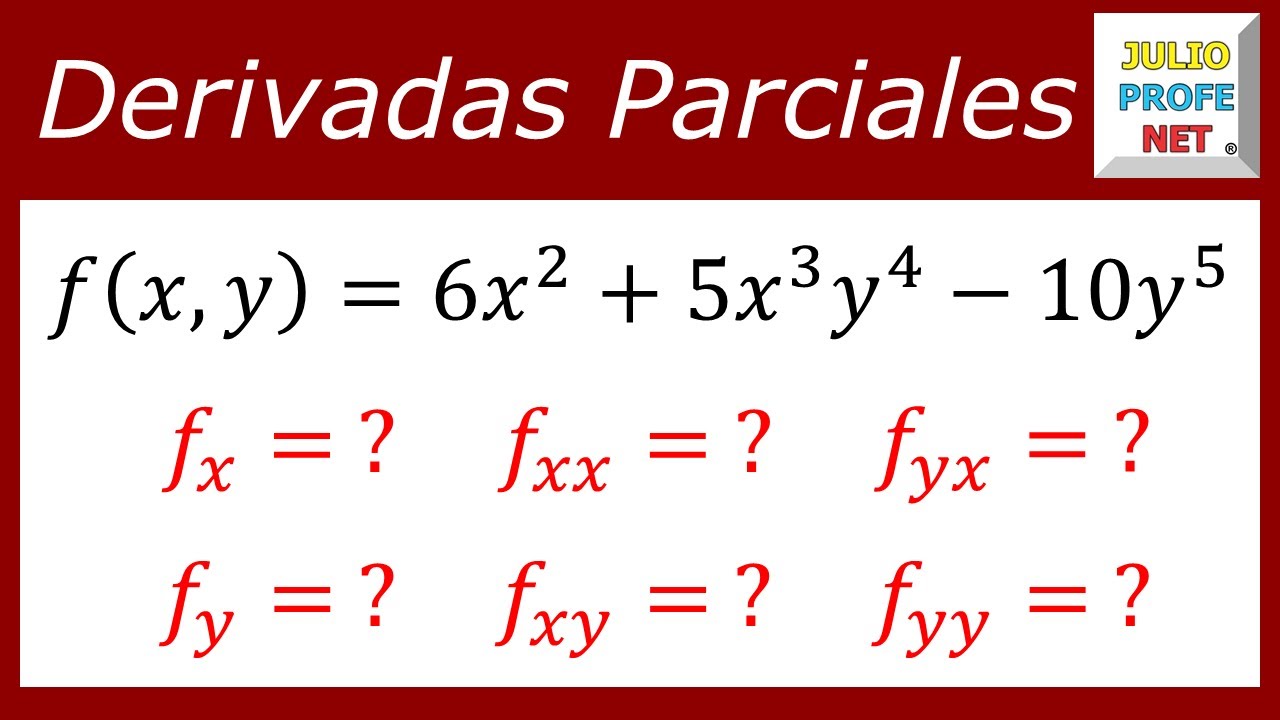Ejemplo 1. Encuentre las derivadas parciales de la función de primer orden z (x,y) = x²y - 3xy + 5y Solución: Sea entonces la función: z = x 2 y − 3 x y + 5 y Dependiendo de la variable que elijamos, podemos obtener diferentes derivadas parciales en conjunto, y a menudo lo hacemos. Ejemplo 4.14 Calcular las derivadas parciales a partir de la definición Utilice la definición de la derivada parcial como límite para calcular ∂ f/ ∂ x y ∂ f/ ∂ y para la función f(x, y) = x2 − 3xy + 2y2 − 4x + 5y − 12.
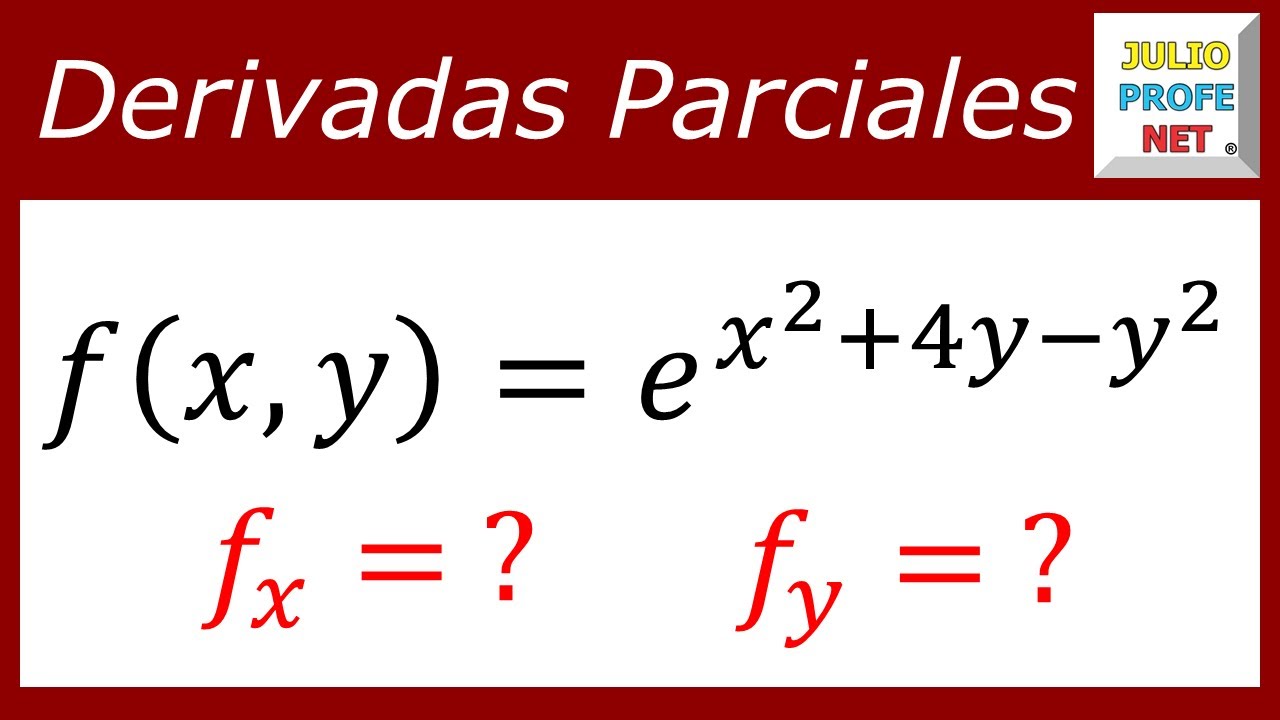
DERIVADAS PARCIALES Ejercicio 7 YouTube
La derivada parcial de la función z = f (x, y), respecto de x se define como: Ahora bien, hay varias maneras de denotar a la derivada parcial de una función, por ejemplo: La diferencia con la derivada ordinaria, en cuanto a notación, es que la d de derivación se cambia por el símbolo ∂, conocido como "D de Jacobi". [toc] Solucion: Como fx(x; y) = 9x2y 4xy2, luego: 2) y fy(1; 2). fx(1; 2) = 34 Como fy(x; y) = 3x3 4x2y + 3y2, luego: fy(1; 2) = 23 2. Sea z = f(x; y) = ln(x2 + y). Determinar fx(1; 2) y fy(1; 2). Determinar las segundas derivadas parciales: fxx, fxy, etc. Solucion: @f 2x 2 fx(x; y) = (x; y) = . Luego, fx(1; 2) = @x x2 + y 3 @f 1 1 fy(x; y) = (x; y) = . ¿Qué es la derivada parcial, cómo la calculas y qué significa? Antecedentes Derivadas (ordinarias) Funciones multivariables Gráficas de funciones multivariables Qué vamos a construir Para una función multivariable, como f ( x, y) = x 2 y , calcular las derivadas parciales se ve algo como esto: Curso Completo: https://www.youtube.com/playlist?list=PL9SnRnlzoyX2-qH2lY3o5Lhv9f6za9o9AEjercicios resueltos de cálculos de derivadas parciales para funcione.
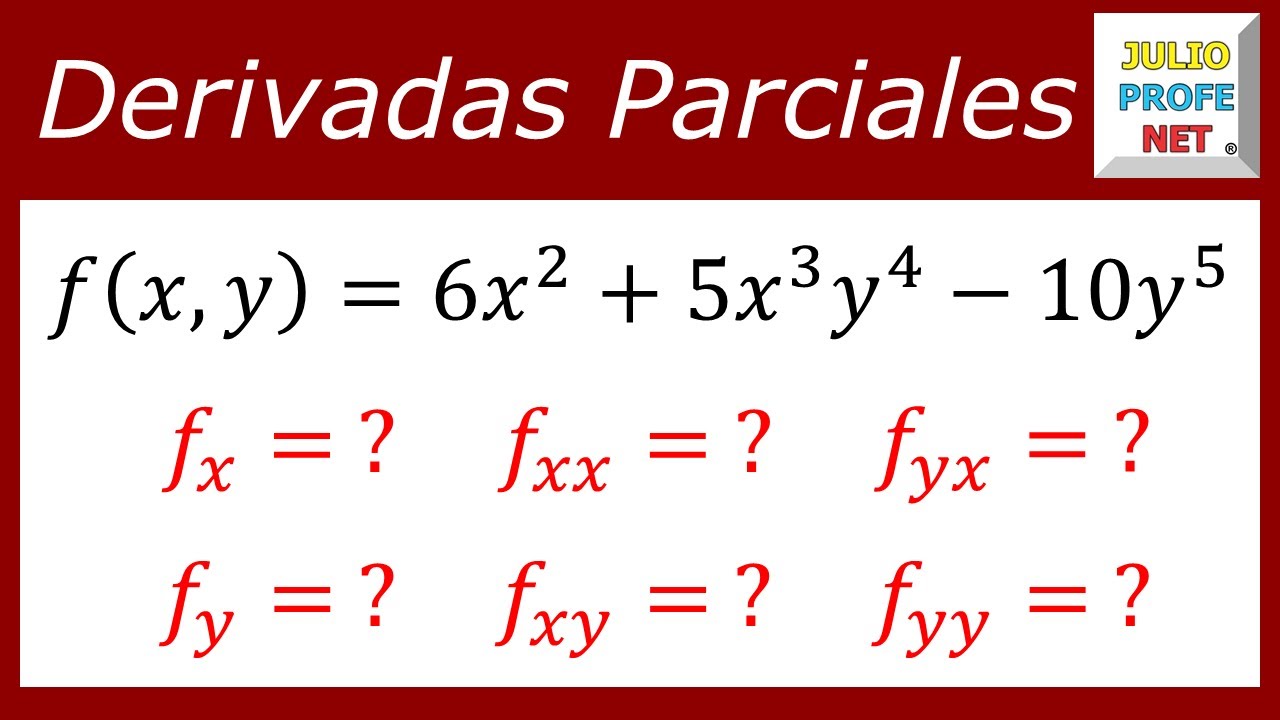
DERIVADAS PARCIALES Ejercicio 11 YouTube
Derivadas parciales básicas. ¿Qué es ∂ f ∂ x ? ¿Atorado? Revisa artículos/videos relacionados o usa una pista. Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más. Khan Academy es una organización sin fines de lucro, con la misión de proveer una. Encontrar derivadas de funciones de dos variables es el concepto clave en este capítulo, con tantas aplicaciones en matemáticas, ciencias e ingeniería como diferenciación. Ejemplo de derivadas parciales de primer orden o primera derivada con respecto a x y primera derivada con respecto a y.Curso completo de Derivadas Parciales:. En el ejemplo de arriba, observa que las dos derivadas parciales mixtas ∂ 2 f ∂ x ∂ y y ∂ 2 f ∂ y ∂ x son iguales. Esto no es una coincidencia: sucede para casi cualquier función que encontrarás en la práctica. Por ejemplo, observa lo que sucede con el término general de un polinomio, x n y k :

Derivadas Parciales Ejemplo 3 YouTube
12.3: Derivadas Parciales. Dejar y ser una función de x. Hemos estudiado con gran detalle la derivada de y con respecto a x, es decir dy dx, que mide la tasa a la que y cambia con respecto a x. Consideremos ahora z = f(x, y). Tiene sentido querer saber cómo z cambia con respecto a x y/o y. Para la derivada parcial con respecto a h mantenemos r constante: f' h = π r 2 (1)= π r 2. (π y r2 son constantes, y la derivada de h con respecto a h es 1) Dice "como solo cambia la altura (en la menor cantidad), el volumen cambia en πr2". Es como si agregamos el disco más delgado en la parte superior con un área de círculo de π r 2 .
Como muestran estos ejemplos, cada derivada parcial en un punto surge como la derivada de una función de una variable definida fijando una de las coordenadas.. Debido a la conexión entre las derivadas de una variable y las derivadas parciales, a menudo usaremos la notación de estilo Leibniz para denotar derivadas parciales escribiendo. Por lo tanto, podemos fácilmente tomar derivadas parciales de derivadas parciales y así sucesivamente. Por ejemplo, la derivada x-parcial de , denotado , es -y 2 sin (xy). Del mismo modo: = = = = Tenga en cuenta que . Resulta que este proceso de intercambiar el orden de las variables con respecto a las cuales tomamos derivadas parciales da la.

Derivadas parciales de orden superior con raíz Ejemplo 1 YouTube
Derivadas parciales El objetivo principal de este capítulo es explicar cómo se extiende el concepto de derivada de una función de una variable a campos escalares de varias variables. Ahora estamos listos para definir derivadas de funciones de más de una variable. Primero, recordemos cómo definimos la derivada, f ′ (a), de una función de una variable, f(x). imaginábamos que estábamos caminando por el x eje -eje, en la dirección positiva, midiendo, por ejemplo, la temperatura en el camino. Denotamos por f(x) la temperatura a x.