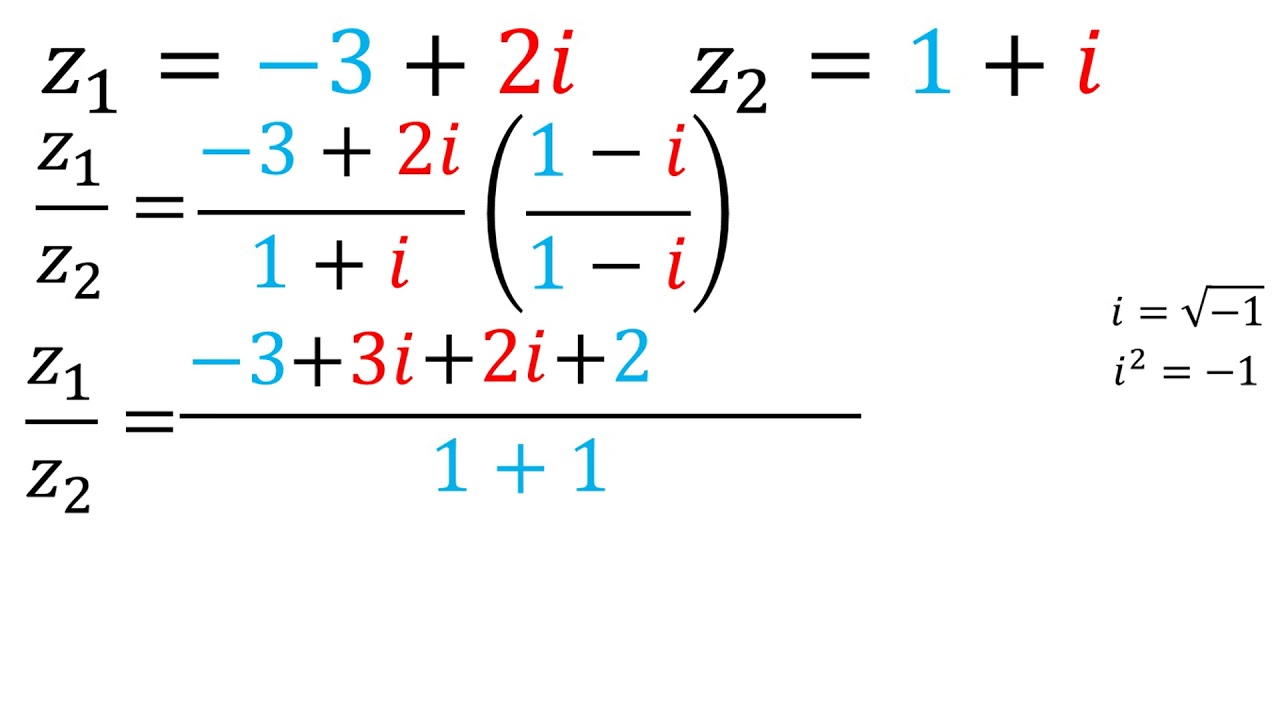Ejercicios de división de números complejos resueltos. Los siguientes ejercicios usan el proceso detallado arriba para resolver las divisiones de números complejos. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta. Calculadora gratuita de números complejos - Simplificar expresiones complejas utilizando reglas algebraicas paso por paso

División de números complejos ejemplo 4 de 4 Álgebra Vitual YouTube
Transcripción del video. divide 63 y entre 75 y muy bien queremos hacer una división de números complejos pero también queremos que el resultado sea un número complejo es decir que sea de la forma un real más un imaginario o sea un real por y vale bueno para hacer esto déjame primero reescribir esta expresión como una fracción el. Dividir un número complejo entre un número real es simple. Por ejemplo: 2 + 3 i 4 = 2 4 + 3 4 i = 0.5 + 0.75 i. Encontrar el cociente de dos números complejos es más complejo (¡jaja!). Por ejemplo: = 20 − 4 i 3 + 2 i = 20 − 4 i 3 + 2 i ⋅ 3 − 2 i 3 − 2 i. Multiplicamos ambos lados por el conjugado del denominador, que es un. Ejemplos de cómo dividir números complejos. ejemplo 1: Divida los números complejos a continuación. El primer paso es escribir el problema original en forma fraccionaria. Dado que nuestro denominador es 1 + 2i, su conjugado es igual a 1 - 2i. Recuerda cambiar solo el signo del término imaginario para obtener el conjugado. Breve explicación con ejemplos de la forma de dividir números complejos, dentro del curso de números complejos.Curso completo de Números Complejos:https://ww.

Division De Numeros Complejos V3 Youtube Otosection
Curso: Precálculo > Unidad 3. Lección 3: Complejos conjugados y división de números complejos. Introducción a los conjugados de números complejos. Conjugados de números complejos. Conjugados de números complejos. Dividir números complejos. Divide números complejos. Repaso de división de números complejos. Prueba de unidad. Comprueba tu comprensión de Números complejos con estas % (num)s preguntas. Inicia la prueba. Este tema cubre: - Sumar, restar, multiplicar y dividir números complejos - Plano complejo - Valor absoluto y ángulo de números complejos - Coordenadas polares de números complejos. Transcripción del video. tenemos aquí esta expresión peliaguda pero en realidad lo único que queremos hacer es dividir estos dos números complejos este número complejo en azul y este número complejo en verde de hecho ya nos los graficaron por acá así que veamos ustedes puede notar que estos de hecho los dos números están en forma. Si quieres puedes comprobar aquí la resolución. Para dividir dos complejos se puede hacer tal como acabamos de aprender, o bien se multiplica el numerador y el denominador por el conjugado del denominador, así el denominador pasará a ser un número real. Finalmente se separan la parte real y la parte imaginaria. EJEMPLO 2: Como verás hemos.
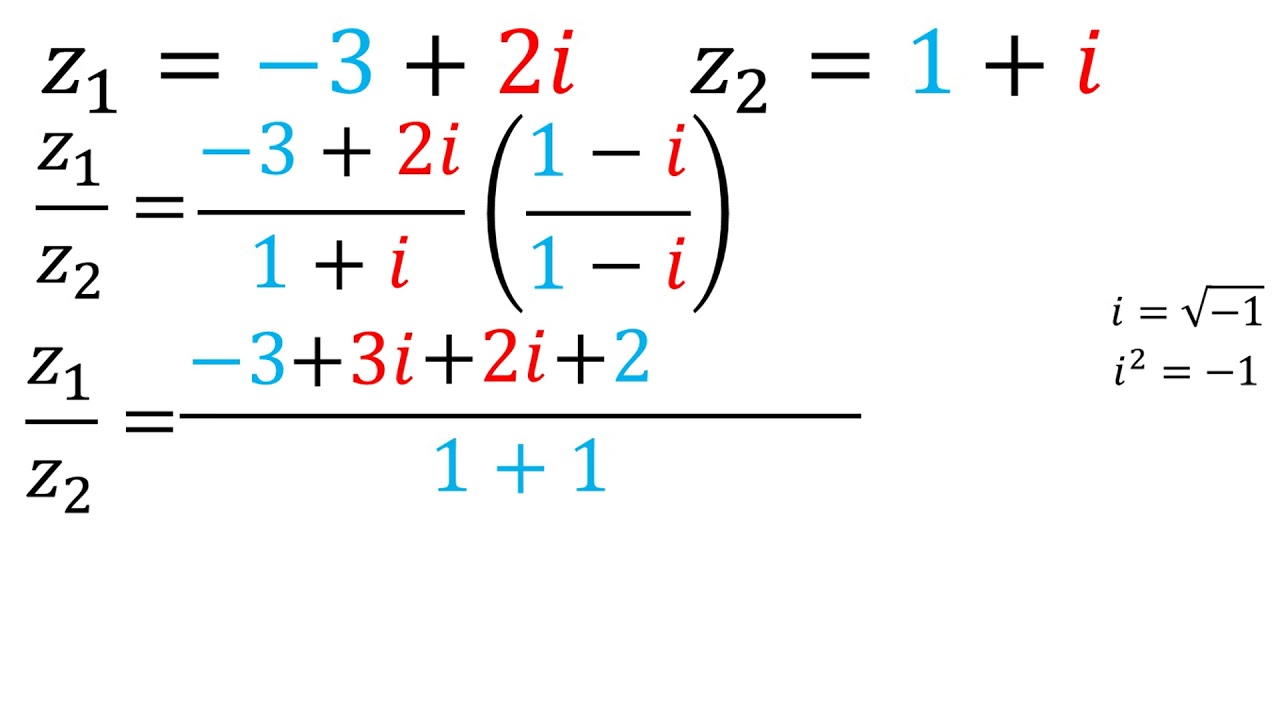
División de números complejos Ejemplo 1 YouTube
División de números complejos en forma polar. La división de dos números complejos es otro número complejo tal que: Su módulo es el cociente de los módulos. Su argumento es la diferencia de los argumentos. 6 45° : 3 15° = 230°. Aprendé RÁPIDO y FÁCIL cómo resolver una DIVISIÓN de NÚMEROS COMPLEJOS con los profesores Adrián y Cristina🎥 Si querés ver el curso completo de NÚMEROS COMP.
División de números complejos e imaginarios explicados paso a paso de forma sencilla. Usamos el concepto de complejo conjugado de un número complejo. Resolve. Ejercicios resueltos para aprender a dividir números complejosFacebook:https://www.facebook.com/TuProfeEnLineaPeru/Visita: www.tuprofeenlinea.com#numeroscomp.

División de números complejos v3 YouTube
Anterior: https://youtu.be/fZTpDnNAnnkSiguiente: https://youtu.be/hrpXt_BbX9wEn este video veremos cómo dividir dos números complejos, con ejercicios resuelt. Podemos dividir rápidamente dos números complejos dados en su forma polar, z1 = pα entre z2 = qβ, donde p y q son los módulos y α y β los argumentos respectivos, donde q ≠ 0. Usando las identidades del seno y coseno de las diferencias podemos demostrar pα qβ = (p q)α − β. Esto es, el cociente es un número complejo con.