ECUACIONES MATRICIALES Ejercicios Determina la matriz X que verifica la ecuación A·X = X - B siendo: 0 0 0 = ( 0 −1 0 1 0 1 0) y B = ( 0 1 1 ) 0 0 −1 −1 Considera la matriz C = ( −1 0 · X - X = 2I (I 1 −1 −1). Calcula la matriz X que verifica: 0 0 es la matriz identidad de orden 3) Sean las matrices: = (2 −1 0 2 −2 ECUACIONES MATRICIALES. Despejar X en cada ecuación. X·A + B = C AX + BX = C AX + 3X = C (AX + B)- 1 = C VER VIDEO https://youtu.be/_OW5knYefbM Multiplicamos. por la derecha, ambos miembros por A−1 X·A+B=C;X·A=C−B Identidad ⏞ ;X·A·A−1 ⏞ =(C−B)·A−1;X=(C−B)·A−1

Ecuaciones matriciales de la forma AX+B=C. Matemáticas 2 bachillerato
a) Para calcular ABC, se calcula primero el producto AB y el resultado se multiplica a la derecha por la matriz C. 2 -1 2.0+(-1)4 2.1+(-1)(-2) -4 4 AB = ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎝ 3 2 ⎠ ⎝ 0 1 ⎞ ⎛ 4 -2 ⎠ = ⎝ 3.0+2.4 3.1+2(-2) ⎠ = ⎝ 8 -1 ⎠ ECUACIONES MATRICIALES ⎜ 1 ⎛− 4 1. Dadas las matrices A 3 =⎜ 1 1 0 ⎜ 1 ⎟ 0 ⎟⎞ 1 ⎛ 27 13 ⎞ ⎟ ⎜ ⎠ ⎟ 1 Sol: X = ⎜ 2 2 ⎟ ⎜ − 23 − 13 ⎟⎟ ⎜ ⎝ 2 2 ⎠ y B ⎛− ⎞ 1 ⎜ ⎟ = ⎜ 1 ⎟ ⎜ ⎝ ⎠ 2 ⎟ 4. Dadas las matrices Resuelve la ecuación matricial: A·X=B ⎛ 3 ⎞ ⎜ ⎟ ⎜ 5 ⎟ ⎜ = ⎜− 4 ⎟ 5 ⎟ ⎜ 14 ⎟ ⎜ ⎟ ⎝ 5 ⎠ Sol: X 2. Dadas las matrices ⎛ 1 = ⎜⎜ ⎝ 3 ⎞ Una ecuación matricial es una ecuación cuya incógnita es una matriz. Para poder resolver una ecuación matricial, tendremos que sumar, restar y multiplicar matrices y calcular matrices inversas. Un ejemplo de una ecuación matricial es La incógnita de la ecuación es la matriz Y la solución de la ecuación es A(cu) = cAu. Definición 2.3.2: Matrix Equation. Una ecuación matricial es una ecuación de la forma Ax = b, donde A es una m × n matriz, b es un vector en Rm, y x es un vector cuyos coeficientes x1, x2,., xn son desconocidos. En este libro estudiaremos dos preguntas complementarias sobre una ecuación matricial Ax = b:
.gif)
MATRICES MATEMÁTICAS 2 BACHILLERATO EJERCICIOS RESUELTOS PDF
Fundamentos del Álgebra Matricial (Hartman) 2: Aritmética Matricial Ecuaciones matriciales En esta página aprenderás qué son y cómo resolver las ecuaciones matriciales. Además, encontrarás ejemplos y ejercicios resueltos de ecuaciones con matrices. Sumario 1. ¿Qué son las ecuaciones matriciales? 2. Cómo resolver ecuaciones matriciales. Ejemplo: 3. Ejercicios resueltos de ecuaciones matriciales Una ecuación matricial es una ecuación cuya incógnita X X es una matriz. Por ejemplo, Existen varias formas de resolver una ecuación matricial, pero la más habitual es utilizar las matrices inversas de las matrices implicadas. Si la matriz A A es regular (tiene inversa), multiplicando por la izquierda en la ecuación por su inversa. 6 Cap tulo 1. Propiedades de matrices y determinantes 2) Se consideran las matrices A= 1 1 1 1 ; B= 0 1 ; C= 0 @ 2 2 2 2 4 4 1 A: a)Calcular la matriz M= AtA BBt, donde At y Bt representan las matrices traspuestas de Ay B, respectivamente.

Ecuaciones Matriciales PDF
9 Aplicar las transformaciones elementales al cálculo del rango de una matriz, la inversa de una matriz y la resolución de sistemas de ecuaciones lineales. I.1. OPERACIONES CON MATRICES. REPASO I.1.1. Definiciones Antes de presentar las operaciones matriciales y sus propiedades se verán unas definiciones: Definición. dispuestos en es la fila y Para resolver las ecuaciones matriciales hay que despejar la matriz X, pero teniendo en cuenta las propiedades de la multiplicación de matrices, como: La multiplicación de matrices no tiene la propiedad conmutativa, por lo que el resultado de A.B no es el mismo que B.A: El elemento neutro de las matrices es la matriz identidad, es decir, al.
MATEMÁTICAS CCSS 1o DE BACHILLERATO. Las ecuaciones matriciales son aquellas en que todos los elementos son matrices. Para resolver las ecuaciones matriciales debemos despejar la matriz X, teniendo en cuenta las propiedades de la multiplicación de matrices. La multiplicación entre matrices no admite la propiedad conmutativa. SOLUCIONES Halla las matrices X e Y que verifiquen el sistema: + =(1 4) 2 0 −1 − =( ) { 1 0 Solución Sumamos las dos ecuaciones: 2 + =(1 4) 2 0 2 2 3 ⇒3 = ( 1 −1 − =( ) { 1 0 ) ⇒ = ( 1 3 ) 3 0 1 0
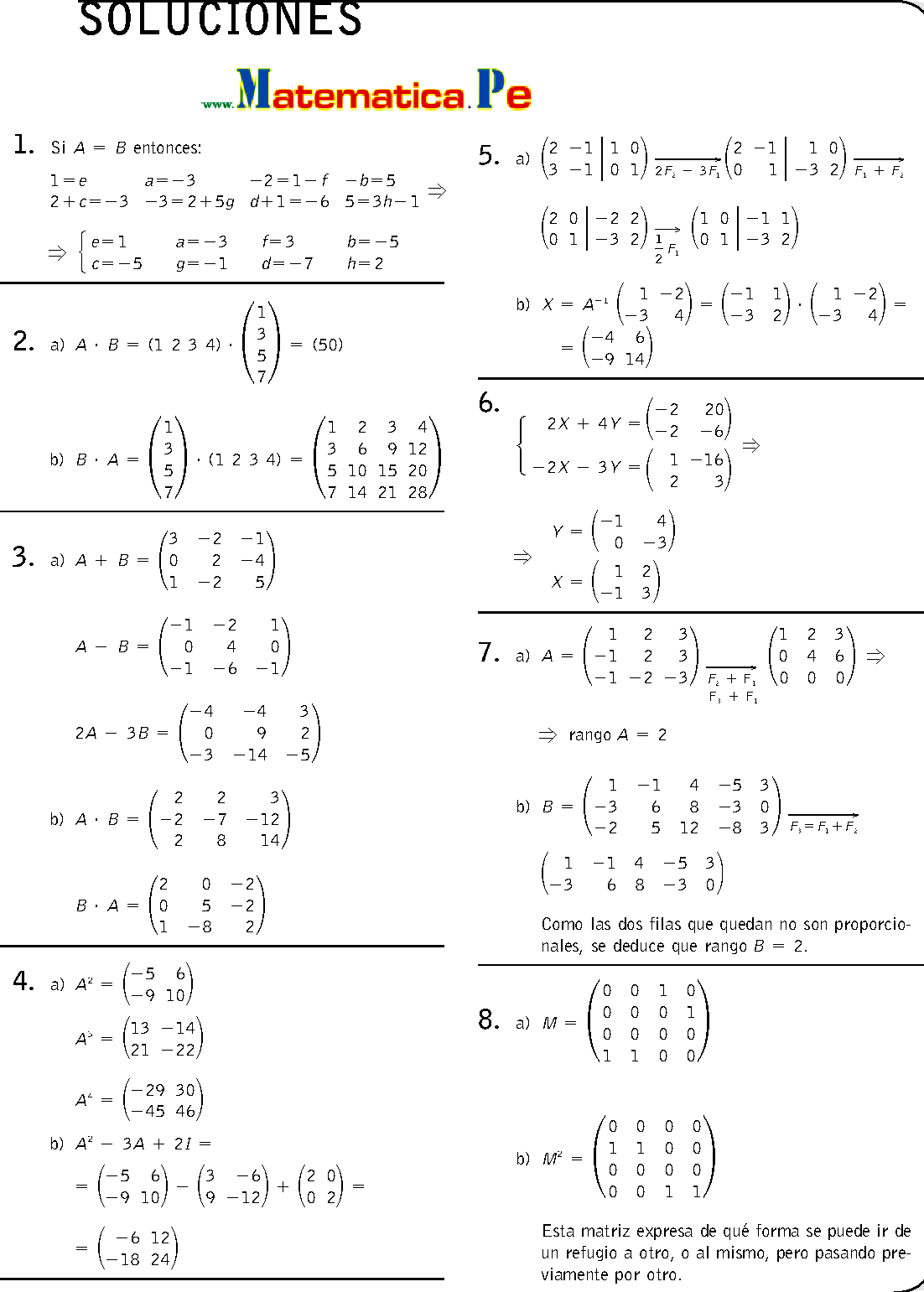.gif)
MATRICES MATEMÁTICAS 2 BACHILLERATO EJERCICIOS RESUELTOS PDF
Sumando las dos ecuaciones, queda: o 2/3 1 Despejamos Y en la 22 ecuación: o 1/3 2 1 2 o 1 2/3 Por tanto, X — 1 o 1 o 2/3 1 -1/3 o Calcula X tal que x— B2 _ 2 4 o o 2 o B, siendo: —1 1 1 1 o 132 B + 132 o o 2 1 o 2 1 3 o 1 o 1 2 o 1 2 o o 1 o o 1 o 2 1 1 Determina los valores de m para los cuales (5/2)m + 1 o o o verifique X2 — o. o 2 1 o Resuelva el sistema de ecuaciones usando matrices: Escriba la matriz en la izquierda como el producto de coeficientes y variables. Primero, encuentre la inversa de la matriz coeficientes. La inversa de es. Enseguida, multiplique cada lado de la ecuación matriz por la matriz inversa . Ya que la multiplicación de matrices no es conmutativa, la.

.gif)

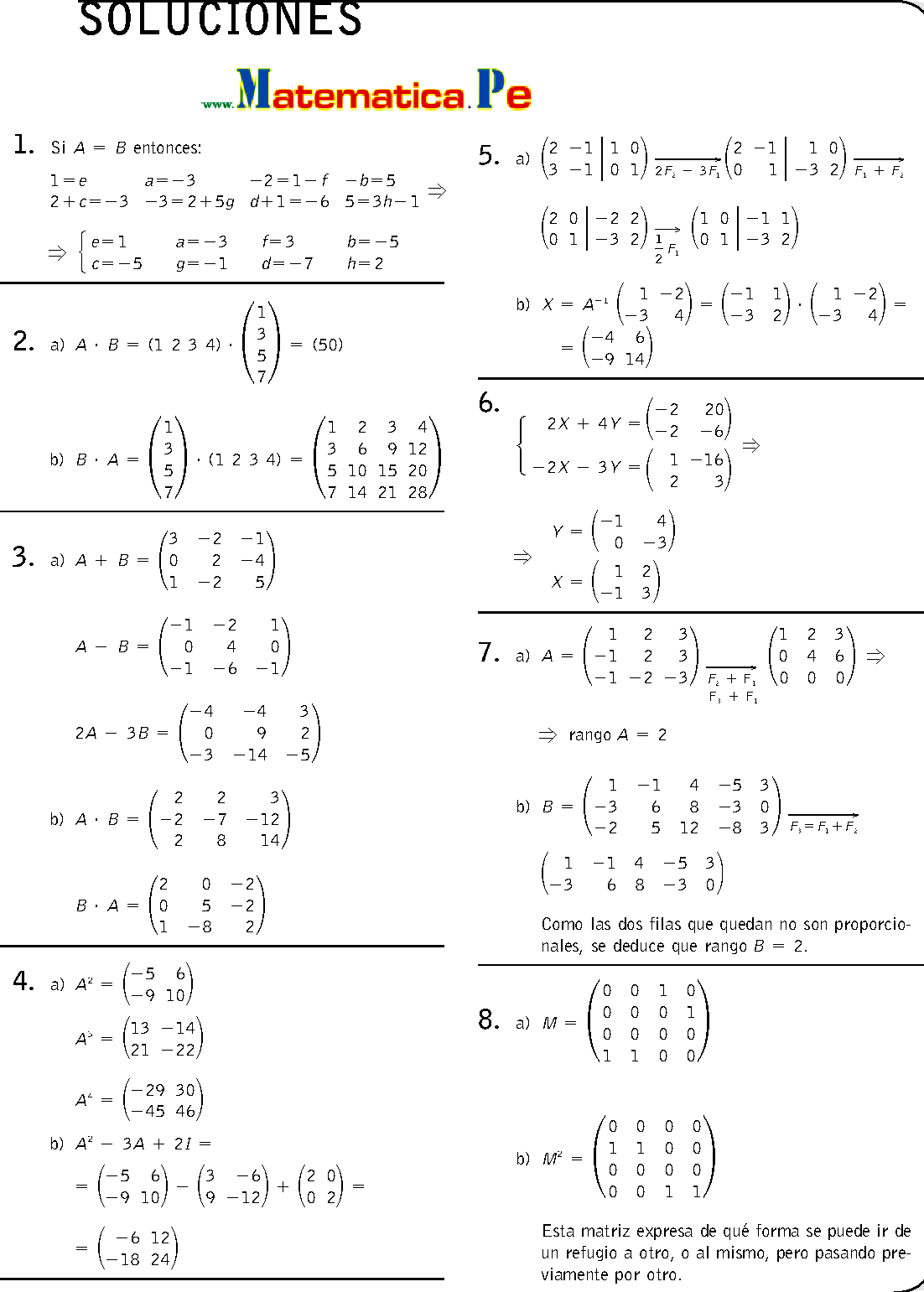.gif)
