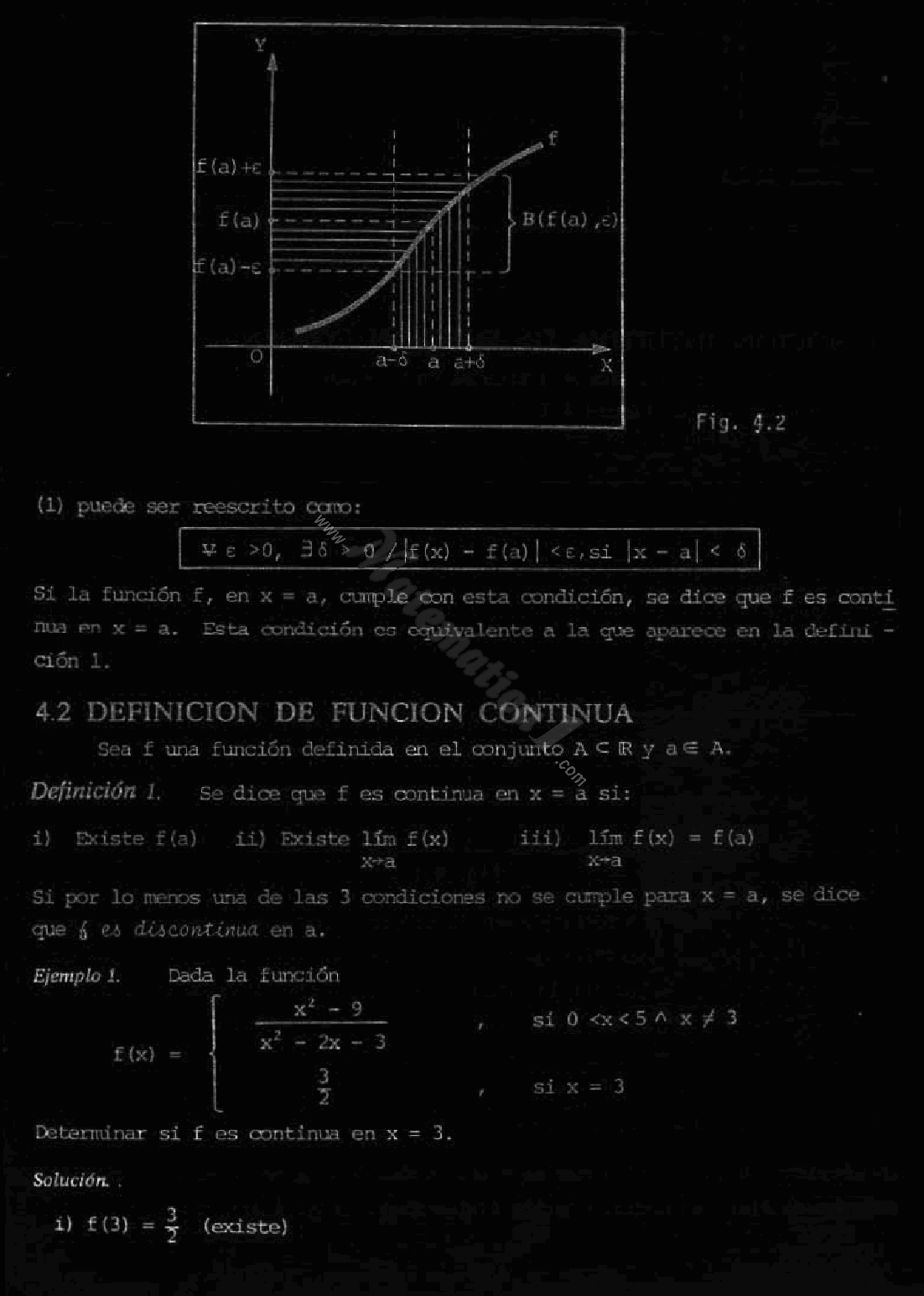
Halla los puntos de discontinuidad, si los hay, de las siguientes funciones: a) Continua. x2 + 2x + 3 x2+2 d) Continua. f) Continua. a) ¿Cuál de las siguientes gráficas corresponde a una función continua? b) Señala, en cada una de las otras cinco, la razón de su discontinuidad. a) Solo la a). b) b) Rama infinita en x = c) Rama infinita en x = 3 lím x x Solución: Hay que ver que para cualquier > 0, existe > 0 tal que si x−3 , entonces − 2 1 1 x Como 2x−4)−2 2x−6 2x− 6 (transformando la desigualdad) 6− 2x 6+ 2 3 2 3 + −x Por tanto, tomando 2 se cumple que . Luego, efectivamente, el límite vale 2.
.gif)
CONTINUIDAD DE FUNCIONES EJERCICIOS RESUELTOS PDF
32 EJERCICIOS de LÍMITES de FUNCIONES y CONTINUIDAD Calcular los siguientes límites no indeterminados 1: lim 1 lim x 1 x +2 - lim x 4x +3 x→ 3 x→ 3 x→ 4 - lim f) x→ e 1+ln x lim log x g) x→0,1 lim h) x→ - 2 x 3 3x - 2 +4x lim d) x→ 1 lim i) x→ 0 + x 2 +4x x lim e) x→ 3x +5 lim 1 j) x→ 4 x 2. 1. Concepto de continuidad Intuitivamente, una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, sin levantar el lápiz del papel. Ejemplo de función continua: f (x) = x3 f ( x) = x 3. Gráfica: Ejemplo de función no continua: f (x) =1/x f ( x) = 1 / x. Gráfica: Definición formal: Encuentra los valores de a y b pava que la función sea continua y su grati- ca pase por el origen de coordenadas. Para que la gráfica de pase por el origen de coordenadas, ha de ser O, es decir. b O Para que la función sea continua (para x 1 es una función continua), tenemos que: lím .f(x) lím .f(x) lím (2x2 + ax) 2 + a lím (In x Ejercicios resueltos de continuidad | Superprof Ejercicios y problemas de continuidad con soluciones Apuntes Escolar Matemáticas Funciones Ejercicios resueltos de continuidad Temas Continuidad de funciones Continuidad en x=0 Demuestra la continuidad donde se indica Calcular valores para garantizar la continuidad

Límites de funciones, continuidad ejercicios resueltos PDF
1. ≠ Dada f(x) = ⎪ ⎨ x ⎪ ⎩ 1 si x = 0 se pide: a) Representación gráfica. b) Estudiar analíticamente la continuidad lateral en x=0 c) A la vista del apartado anterior, ¿es continua en x=0? 2. Ídem con f(x) = x 3. Estudiar la continuidad de las siguientes funciones: a) f(x) = + 1 − 2 = 2x b) f(x) 2 x − 5x + 6 2 x + x c) f(x) = Ejercicios propuestos sobre continuidad de funciones. Establézcase si las funciones dadas son o no contínuas en el punto = − a. f ( x ) 4 x 2 x + 12 2 3 x c. g ( x ) = x − 2 = ) x ( h e. x − 3 = [ ] g. t ( x ) x (parte entera de x) 3 − i. t 8 m ( x ) = − 2 8 − x 4 si ≠ 2 k. f ( x ) = x − 2 2 si = x 2 − 3 x + 4 Entender cómo se comportan las funciones cuando se aproximan a ciertos valores es muy importante para muchas aplicaciones reales. En este documento se trabajarán ejercicios referidos a los conceptos de límite de una función, continuidad de funciones y asíntotas de las mismas. Límites de funciones 2o Evaluación. Continuidad Continuidad de una función Una función f(x) es continua en el punto x=a, si existe el límite cuando x tiende a "a" y coincide con el valor de la imagen de "a", f(a) Es continua si = f(a) Una función es continua en un punto x=a si se cumplen las tres condiciones siguientes: y f(a)
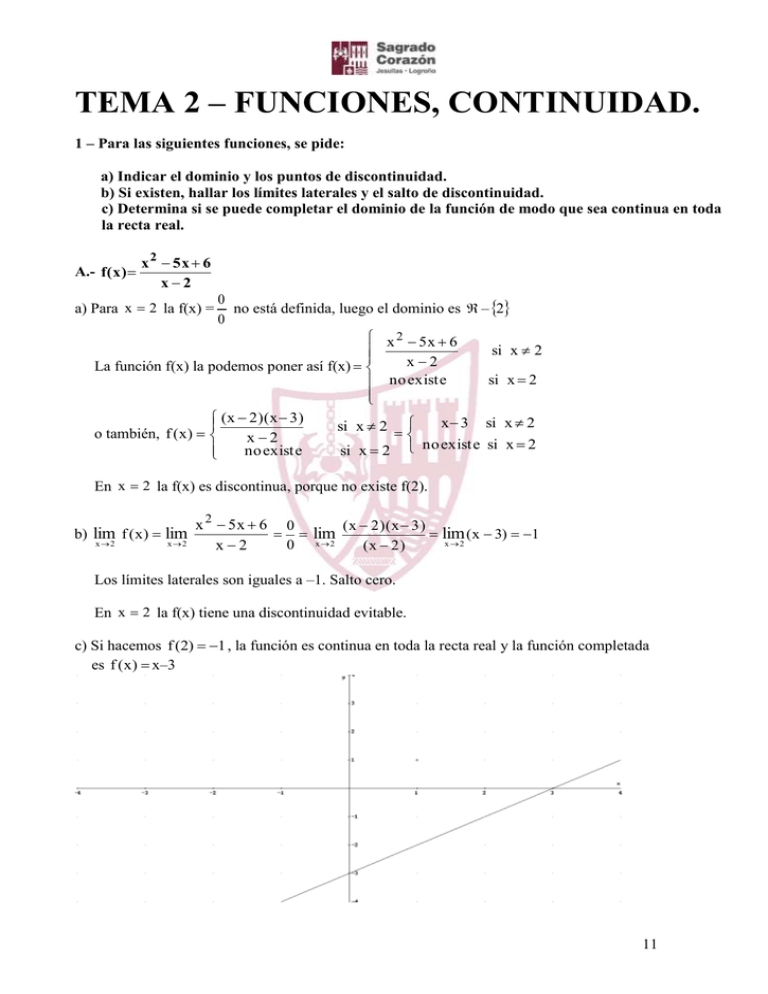
TEMA 2 FUNCIONES, CONTINUIDAD. 1 Para las siguientes
Problemas Resueltos sobre Límites y Continuidad Repaso de Problemas típicos x 3 − 2 x 2 lim x → 2 x − 2 2 lim x →∞ x 3 x 2 x + 1 x 3 lim x 2 + 1 − x 2 2 2 2 + x 5 + 2 x 3 + 3 − →∞ 4 lim x + x + 1 − x − x − 1 x →∞ 2 x 5 lim → 0 2 x 2 + x + 1 − 6 e n ( 3 x ) lim 2 − 3 x 7 s e n ( s e n ( x ) ) 8 lim x →0 1 EJERCICIOS DE CONTINUIDAD CON SOLUCIÓN 1o Bachillerato. Matemáticas I Calcula el limy 1 lim de las siguientes funciones definidas a trozos: 2 3 5 x 3 x 1 6 x 3 x 2 a) f x b )f x c ) f x 9 x 21 9 x 1 x 1 4 x 2 29 x 2 1 Sol: a) 8, -7 b) -3, no existe c) no existe, 30 ln x 2
CÁLCULO DE LÍMITES: GRÁFICAMENTE EJERCICIO 1 : Halla, observando la gráfica de la función f (x),. Tema 5 - Límites y Continuidad - Matemáticas CCSSII - 2º Bachillerato 2 EJERCICIO 4 : Halla los siguientes límites, observando la gráfica de la función f (x): El cálculo de límites respeta habitualmente las operaciones básicas: si se suman, restan, multiplican, dividen, y se calcula la potencia del límite de dos funciones, da el límite de operar estas dos funciones. Esto es: Si observamos las dos rimerasp ropiedadesp mencionadas, podemos ver que el cálculo del límite de un
.gif)
LÍMITES Y CONTINUIDAD DE FUNCIONES EJERCICIOS RESUELTOS MATEMATICAS 2 BACHILLERATO PDF
PROBLEMA 1 Estudiar la continuidad de la función: x 2 y = f ( x ( , y ) ≠ (0,0) ) y , x 2 + y 2 0 ( x , y ) = (0, 0) SOLUCIÓN Planteamos el estudio del límite en el origen realizando un cambio a coordenadas polares: Así: x = ρ cos ( θ ) y = ρ sen ( θ ) ρ 3 cos 2 sen θ l = lim f ( x , y ( θ ) ( ) ) = lim = lim ρ cos 2 θ sen θ = 0 1 3. Estudia la continuidad de la función f (x) en el punto x=-1. Define la función x 1 para que sea continua. x 2 1 Sol: f (x) si x 1 x 1 2 si x 1 4. Estudia la continuidad de la función f(x)=1/x en x=0. Sol: La función tiene una discontinuidad de salto infinito en x=0. x 1 si x 2 5.
.gif)


.gif)
