Resolver las inecuaciones: a) x2 + 6x - 1 ≤ 3x2 + 3x - 6. b) 3x2 + 4 < x4 + 3x3 + 3x. Solución. a) Al ser una inecuación polinómica de segundo grado, se agrupan todos los términos en un miembro, por ejemplo, si se pasan al primero queda -2x2 + 3x + 5 ≤ 0. -2x2 -3 ± 32 - 4(-2)5 -3 ± 49 -3 ± 7 -1. Solución: [ -1, Inecuaciones Racionales Se trata de una Región Factible Acotada c){ Se trata de una Región Factible No Acotada ( Vértices ( ) ( { Se trata de una Región Factible Acotada d){ ( ) Vértices ( ( { x 0 y 0 x 2 y e) 2 ( x 1 ) y f) 3 x y 1 0 2 x y 3 0
.gif)
INECUACIONES CON VALOR ABSOLUTO EJERCICIOS RESUELTOS Y PARA RESOLVER PDF
La solución de una inecuación de este tipo puede ser: Un conjunto de números reales que se suele expresar en forma de intervalo. Cualquier número real. Ningún número real. Entonces se dice que no tiene solución. EJERCICIOS RESUELTOS 1o) Resuelve: 3x + 12 > 0 8x − 16 ≥ 0 5x − 10 < 0 9x + 27 ≤ 0 SOLUCIÓN: 3x > − 12 > − 12 3 4 > − x ⇒ Ejercicios de inecuaciones Ejercicios de inecuaciones Resuelve 5 d) las 12 siguientes inecuaciones de primer grado: b) 3 c) 3 5 e) f) Resuelve las siguientes inecuaciones de segundo grado: 5 0 b) 3 5 12 0 c) d) 9 14 0 e) 1 1 12 0 f) Resuelve las siguientes inecuaciones polinómicas: d) 2 4 0 Resuelve: 1 4 + 12 3 − 64 2 > 0 sacamos factor común x Como el primer factor es siempre positivo, sólo tendremos que estudiar el signo del 2o factor. 1) Resuelve la siguiente inecuación (pag 67, ejercicio 4a)): 3(x - 5) - 5 > 7(x + 1) - (2x + 3) Resolución: Si nos fijamos se trata de una inecuación de primer grado que para resolver procederemos como si se tratara de una ecuación con la precaución de que si pasamos multiplicando o dividiendo algún número negativo nos cambiará la desigualdad,
.gif)
INECUACIONES EJERCICIOS RESUELTOS PDF
a) Resuelve la inecuación 2 ( x − 3 ) ≤ 4 x + 2 Quitamos el paréntesis efectuando operaciones: 2 x − 6 ≤ 4 x + 2 Transponemos los términos de la inecuación (propiedad 1): 2 x − 4 x ≤ 2 + 6 − 2 x ≤ 8 Despejamos la incógnita. Notamos que el coeficiente de la incógnita es negativo, por tanto aplicaremos la propiedad 3. 1. Inecuaciones Las relaciones numéricas o algebraicas separadas por los signos < (menor), ≤ (menor o igual), > (mayor), ≥ (mayor o igual) se llaman desigualdades. Las desigualdades en las que intervienen variables se llaman inecuaciones; las siguientes desigualdades son inecuaciones: x > y; x ≥ 18; 4y ≥ 32. 4.1. INECUACIONES DE PRIMER GRADO CON DOS INCÓGNITAS 4.2. SISTEMAS DE INECUACIONES DE PRIMER GRADO CON DOS INCÓGNITAS Resumen En muchas ocasiones vas a encontrarte con inecuaciones. Si trabajas con intervalos dirás a < x < b, por ejemplo. Ejercicios resueltos 13 Conocimientos básicos de Matemáticas. Bloque 2. Álgebra. Tema 4. Ecuaciones e Inecuaciones G3w Ana Allueva - José Luis Alejandre - José Miguel González MATEMÁTICA APLICADA- Universidad Zaragoza 2.4-6 Resolver los siguientes sistemas de inecuaciones de primer grado con dos incógnitas: ay) x 2 3
.gif)
INECUACIONES Y SISTEMAS EJERCICIOS RESUELTOS DE MATEMÁTICA 4 ESO PDF
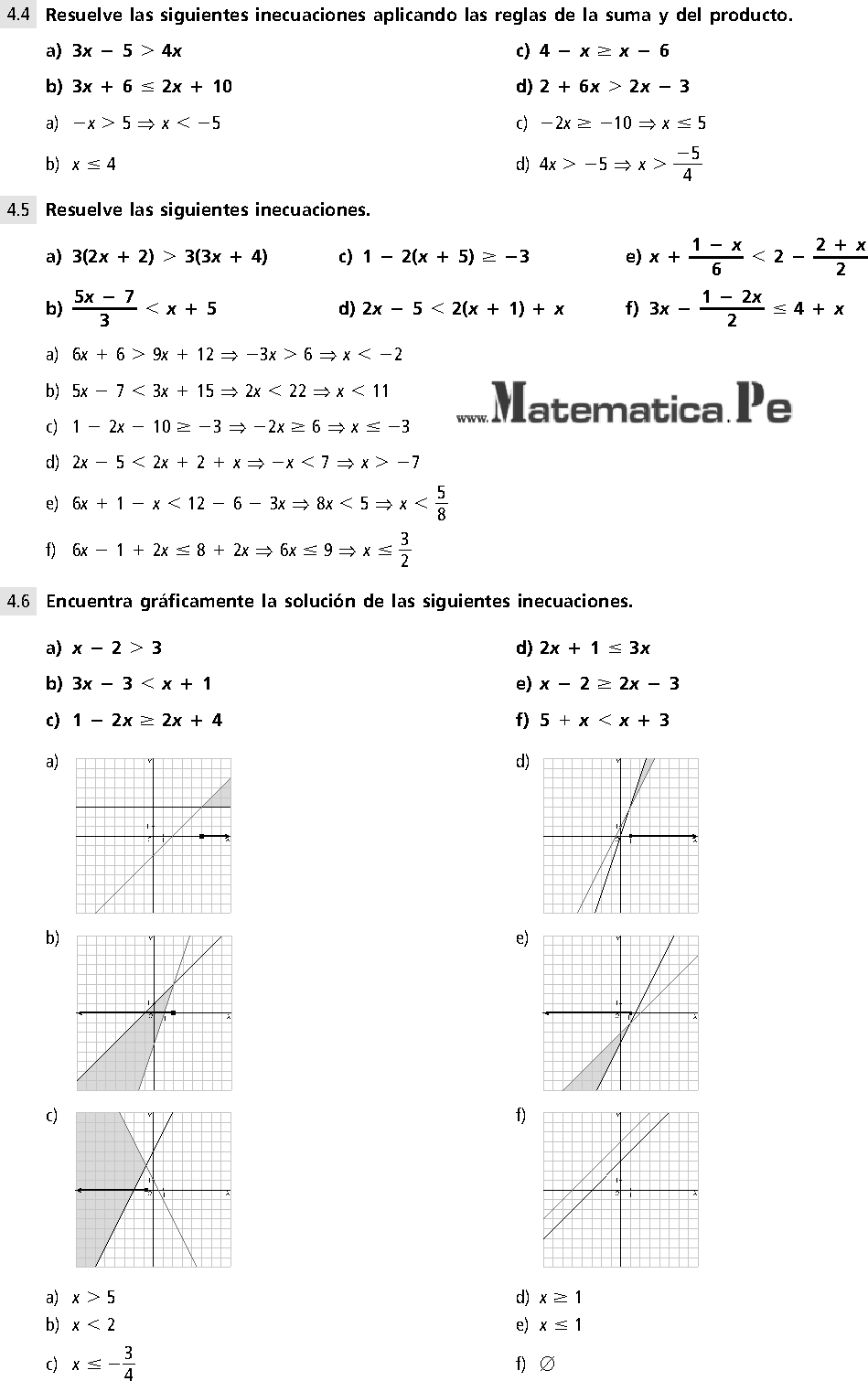
PRIMER GRADO SEGUNDO GRADO resuelto Resuelve x2 - 6x + 8 > 0 1o Igualamos el polinomio del primer miembro a cero y obtenemos las raíces de la ecuación de segundo grado. x2 − 6x + 8 = 0 2o Representamos estos valores en la recta real. Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo: P(0) = 02 − 6 · 0 + 8 > 0 Resuelve las siguientes inecuaciones de primer grado: a) 2 4 0x b) 3 7 5x c) 2 3 x d) x x 3 3 e) 2 5 6 4x x f) 3 5 4 1x x
EJERCICIOS DE INECUACIONES 20 EJERCICIOS de INECUACIONES 4o ESO opc. B Repaso de desigualdades: 1. Dadas las siguientes desigualdades, indicar si son V o F utilizando la recta real. Caso de ser inecuaciones, indicar además la solución mediante la recta R y mediante intervalos: 4>-3 5<-6 4‡6 3<3 3£3 x>0 x£-3 2x<8 5 2. Solución: Solución: LISTADO: INECUACIONES Con Respuestas 1) INECUACIONES DE PRIMER GRADO a) ( x - 2 )2 > (x + 2)⋅ ( x - 2) + 8 b) ( x - 1 )2 < x ( x - 4) + 8 c) 3 - ( x - 6) ≤ 4x - 5 d) 3x - 5 - x - 6 < 1 4 12 e) 1 - x - 5 < 9 + x
.gif)
INECUACIONES EJERCICIOS RESUELTOS PDF
Resolver el sistema de inecuaciones ⎪ ⎨ 7 y − 8 > 4 (2 y − 3) ⎪ ⎪ − 4( x + 2) ≤ 0 ⎩. Solución. En primer lugar se resuelve la primera inecuación, para ello se despeja y obteniéndose y > ex + 1. Para representar gráficamente la solución de la primera inecuación dibujamos y = ex + 1 que es la. Ejercicios Inecuaciones lineales Resuelva cada inecuación lineal. 5 x + 1 < 6 d) 2 + 3 x ≤ 8 − x g) x+ 8 ≤ 3 x + 1 j) x − 6 ≤ 18 − 7 x m) 3 x − 4 < x + 6 b) x ≥ 6 − x e) − 3 x + 5 ≤ 4 − x h) 2 x − 6 > 3 x + 1 k) 3 x − 1 ≤ x − 11 n) 3 x − 7 < 5 x + 2 Resuelva cada inecuación lineal: 2 x > 7 − > 3 (2 − 3 x ) d) 5 ( 2 3 x ) b) 2 x + ≥ 1 2 3
.gif)
.gif)
.gif)
.gif)
