Fórmulas de área y volumen de cuerpos geométricos Fórmula de Euler: C + V - A = 2 donde, C= no de caras, V= no de vértices, A= no de aristas EJERCICIOS DE VOLÚME ES Ejercicio no 1.- Expresa en cm3: 1 m3 5 400 mm3 0,003 dam3 Solución: 1 m3 = 1 · 1 000 000 cm3 = 1 000 000 cm3 5 400 mm3 = 5 400 : 1 000 cm3 = 5,4 cm3 We would like to show you a description here but the site won't allow us.
Demostración de las fórmulas de área y volumen usando integrales
Fórmulas de área, perímetro y volumen de figuras del plano y del espacio www.vaxasoftware.com Cuadrado A=a2 P =4a Rectángulo A=b·h P =2b+2h Paralelogramo A=b·h P =2b+2a Rombo En este documento, encontrarás las fórmulas de áreas y volúmenes de las siguientes figuras: Triángulo. Cuadrado. Rectángulo. Trapecio. Paralelogramo. Circunferencia. Elipse. Cubo. Esfera. Cilindro. Cono. Tronco de cono. Más adelante, actualizaré el documento con muchas otras fórmulas. TABLA DE AREAS Y VOLUMENES Cuadrado Triángulo 2 B h A ⋅ = =A a 2 Rectángulo Romboide = ⋅ A B h = ⋅A B h Rombo Trapecio ( ) 2 B b h A + ⋅ = 2 D d A ⋅ = Polígono regular Círculo =2π⋅P R 2 P a A ⋅ = π= ⋅ A R 2 Corona circular 2 π(= ⋅ − A R r 2 2) Sector circular 360 R n A ⋅ ⋅ = π Cubo =6A a 2 =V a 3 Cilindro =2π⋅. B is the area of the base and P is the perimeter of the base. of the base. The sum of the angles in a triangle is 180°. The sum of the angles in an n-sided polygon is. 180 n 2 . n , where n is the number of sides. Ax By C , where A, B, and C are integers, A and B are not both zero, and A is positive. rate, n is the number of compounds per year.

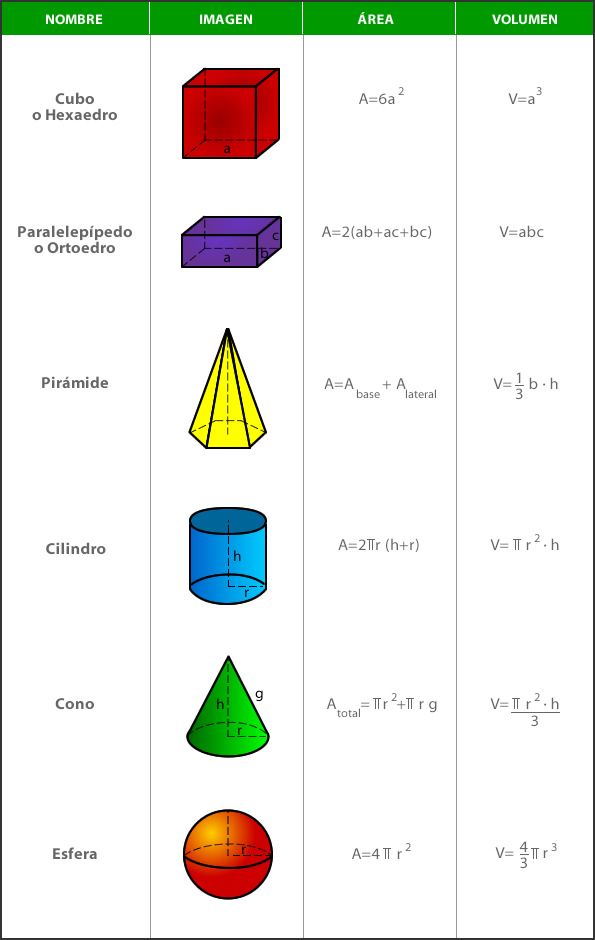
FÓRMULAS DE LAS ÁREAS Y VOLÚMENES DE LOS CUERPOS GEOMÉTRICOS Cuerpos Área… Fórmulas de
1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. To-dos estos objetos son cuerpos geométricos. A lo largo de todos los tiempos se han utilizado estos cuerpos en el arte y en la arquitectura. Área, perímetro y volumen de figuras del plano y del espacio www.vaxasoftware.com A = Área, S = Área, P = Perímetro, V = Volumen Figuras del plano Cuadrado A a2 Ángulo interno 90 P 4a Ángulo externo 90 Núm. diagonales ND 2 Rectángulo A b·h P 2b 2h Paralelogramo A b·h P 2b 2a c2 d2 2(a2 b2) Fórmulas de áreas y volúmenes de cuerpos geométricos A continuación, veremos todas las fórmulas para calcular el área y el volumen de los diferentes tipos de cuerpos geométricos. Sin embargo, si quieres puedes ir directamente al final del post donde encontrarás una tabla con el resumen de todas las fórmulas de áreas y volúmenes. Áreas y Volúmenes de Figuras en el espacio Cubo Ortoedro Circunferencia 62 A a Lat V a 3 2 · · · A ab bc acLat V abc ·· 24·· A r Lat 4··3 3 V r Cilindro Cono Pirámide A rhLat 2··· ·· 2 2 A rg g h r Lat · 2 Base c Lat Perímetro h A

Cuadro de formulas de area y perímetro Geometry Formulas, Math Formulas, Formula Chart, Math
ser capaz de encontrar el volumen de algunos objetos geométricos comunes. Muy a menudo es necesario multiplicar un número denominado por otro. Para ello, multiplicamos las partes numéricas juntas y las partes unitarias juntas. Por ejemplo, 8 in. ⋅ 8 in. = = 8 ⋅ 8 ⋅ in. ⋅ in. 64 in.2 8 in. ⋅ 8 in. = 8 ⋅ 8 ⋅ in. ⋅ in. = 64 in. 2. FÓRMULAS DE LAS ÁREAS Y VOLÚMENES DE LOS CUERPOS GEOMÉTRICOS Cuerpos Área total (AT) Área lateral (AL) Área base/s (AB) Volumen (V) PRISMAS RECTOS h ORTOEDRO c b a CUBO a AT = AL + 2AB AT = 2ab+2ac+2bc AT = 6a2 AL = PB · h AL = 2ac+2bc AL = 4a2 b · a (1) 2 AB = l2 (2) P · ap (3) 2 AB = 2ab AB = 2a2 V = AB · h V = a·b·c V = a3 PIRÁMIDES
3. Si no queremos memorizar las fórmulas para hallar el volumen de los troncos, lo que se hace es utilizar la. semejanza de triángulos y el teorema de Tales. Para hallar el área y el volumen de un huso esférico podemos usar una regla de tres simple directa. Otras fórmulas: Fórmula de Herón. para calcular el área de un. triángulo: Fórmulas de área y volumen de cuerpos geométricos Figura Esquema Área Volumen Esfera A total = 4 r 2 Cubo A = 6 a2 V = a 3 Prisma A = S uma V de A caras = A b h Cilindro A base = r 2 A lateral = 2 r h A total = 2 rh +2 r 2 V = A base. h V = r 2 · h Pirámide A base =A Polígono A lateral =S uma A triáng. A Total =A base +A Lateral 3 A h V.

ÁREAS,PERÍMETROS Y VOLÚMENES FÓRMULAS.pdf Triángulo Formas geométricas
Definir el concepto de distancia y resolver problemas de distancias entre puntos, rectas y planos. 4. Deducir fórmulas que abrevian el cálculo de distancias. 5. Aplicar el producto vectorial y el producto mixto para calcular áreas y volúmenes. 6. Estudiar qué es un lugar geométrico y cómo se determinan los puntos que lo constituyen. S general (6 bis) obtenida en 2.3. Fórmulas gen~ralespara la determinación de áreas y volúmenes. De igual manera, derivando la fórmula (19) con respecto al radio se volveráa obtener el rnis~noresultado anterior. En efecto, sustituyendo en dicha fórmula h por R-z, se tiene la siguiente expresión: V =.




