Fórmulas e identidades trigonométricas Temas Razones trigonométricas Identidades pitagóricas Identidades de la suma y diferencia de ángulos Identidades del ángulo doble y del ángulo medio Identidades para la reducción de potencias Transformación de suma a producto y viceversa Teoremas del seno, del coseno y de la tangente Las fórmulas trigonométricas surgen de las relaciones trigonométricas, pues son las relaciones de donde parten las expresiones matemáticas que permiten el desarrollo de los temas en los que se aplican, podemos contar entre ellos la astronomía, la aviación, la radio, etcétera.
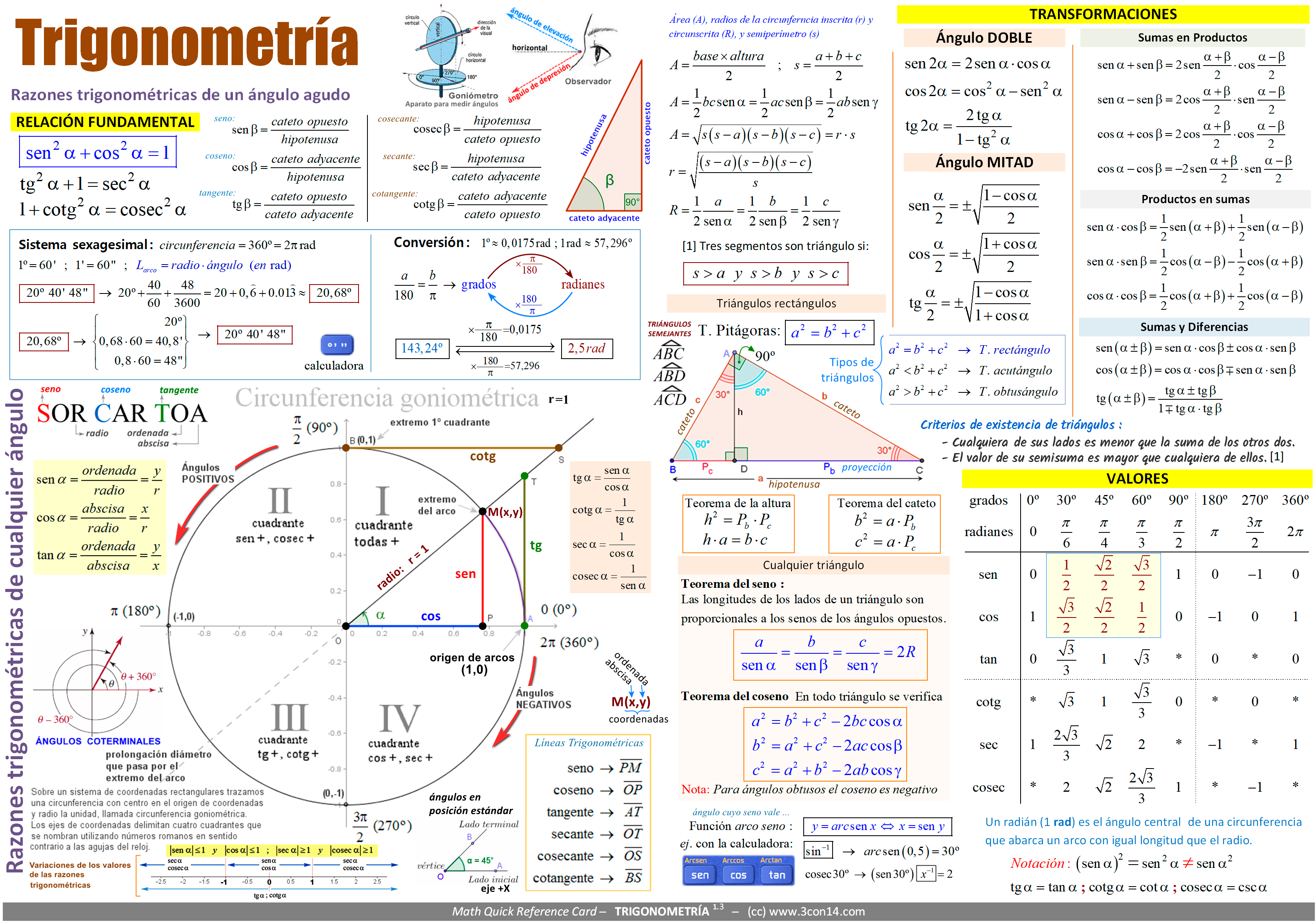
3con14 Matemáticas E · Trigonometría I [Fórmulas]
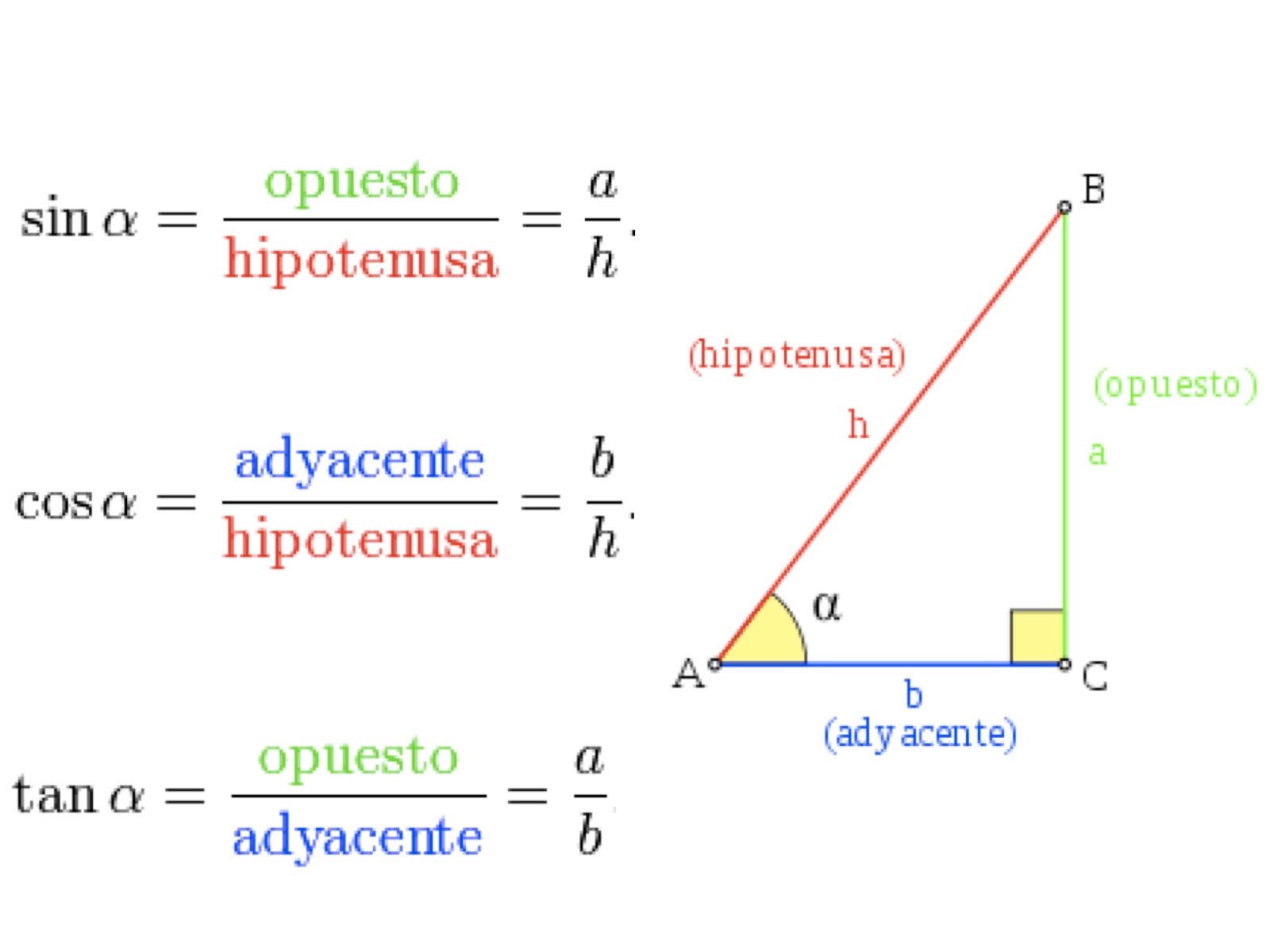
Unidad 3: Funciones trigonométricas. 0/1700 puntos de dominio. Introducción al círculo unitario Radianes La identidad Pitagórica Valores trigonométricos de ángulos especiales Gráficas de sin (x), cos (x) y tan (x) Amplitud, línea media y período Transformar gráficas sinusoidales Graficar funciones sinusoidales Modelos sinusoidales. Este tema cubre: - Definición de funciones trigonométricas en el círculo unitario - Identidades trigonométricas - Gráficas de funciones sinusoidales y trigonométricas - Inversas de funciones trigonométricas y resolución de ecuaciones trigonométricas - Modelar con funciones trigonométricas - Funciones paramétricas Introducción a los radianes adyacente opuesto hipotenusa sin ( A) = opuesto hipotenusa cos ( A) = adyacente hipotenusa tan ( A) = opuesto adyacente A B C En estas definiciones. los términos opuesto, adyacente e hipotenusa se refieren a las longitudes de esos lados. SOH-CAH-TOA: una manera sencilla de recordar las razones trigonométricas En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante. La trigonometría se aplica a otras ramas de la geometría o la geometría analítica en particular geometría plana o geometría del espacio.

Identidades Trigonométricas Fundamentales Mates Fáciles
Ejemplo 1: el seno de 30 grados es 0,50. Esto quiere decir que el lado opuesto al ángulo de 30 grados es exactamente la mitad del largo de la hipotenusa. Ejemplo 2: esta relación se puede usar para encontrar el largo de la hipotenusa en un triángulo que tiene un ángulo de 30 grados con el lado opuesto a ese ángulo que mide 18 cm (7 pulgadas). Las funciones trigonométricas se pueden definir como el cociente entre dos lados de un triángulo rectángulo, asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Aprende. Preparación para triángulos rectángulos y trigonometría. Hipotenusa, opuesto y adyacente. Razones laterales en triángulos rectángulos como función de los ángulos. Utilizar semejanza para estimar la razón entre longitudes laterales. Utilizar razones de triángulos rectángulos para aproximar medidas de ángulos. Usar triángulos rectángulos para evaluar funciones trigonométricas. En secciones anteriores, hemos utilizado un círculo unitario para definir las funciones trigonométricas. En esta sección, ampliaremos esas definiciones para aplicarlas a los triángulos rectángulos. El valor de la función seno o coseno de t t es su valor en t t radianes.
Matemáticas Noveno TRIGONOMETRÍA
FUNCIONES TRIGONOMÉTRICAS: Seno, Coseno, Tangente, Cotangente, Secante, Cosecante | IDENTIDADES TRIGONOMÉTRICAS: Identidades Recíprocas, Identidades Cocientes, Identidades Pitagóricas, Identidades Pares o Impares, Identidades de Suma y Diferencia, Identidades de Suma a Producto, Identidades de Producto a Suma, Identidades de Ángulo Mitad, Identi. Dados los tres lados y análogamente para los otros dos. Dados dos lados y el ángulo que abarcan y el ángulo Dados dos lados y otro ángulo Si conocemos , y el ángulo y aplicando que los ángulos suman y a partir de ahí se sigue como en los casos anteriores. Dado un lado y dos ángulos Si concemos el lado a y los ángulos
Recordamos las razones trigonométricas de los principales ángulos para facilitar el cálculo de la forma polar de un nº complejo o la forma binómica. En la siguiente tabla se resumen las razones trigonométricas de los ángulos del primer cuadrante, ya que el resto se pueden deducir a partir de las propiedades básicas de trigonometría. Fórmulas de la trigonometría. Las relaciones trigonométricas expresan relaciones entre los ángulos y las longitudes de un triángulo; se pueden utilizar para obtener cantidades desconocidas. Puedes verlas en las fórmulas siguientes: sin ( θ) = C O H. cos ( θ) = C A H. tan ( θ) = sin ( θ) cos ( θ) = C O C A. Aqui:

Fórmulas de Trigonometría PDF Triángulo Grafemas
Evalúe ∫cos3xsen2xdx. En el siguiente ejemplo, vemos la estrategia que debe aplicarse cuando solo hay potencias pares de senx y cosx. Para las integrales de este tipo, las identidades. sen2x = 1 2- 1 2cos(2x) = 1 − cos(2x) 2. cos2x = 1 2 + 1 2cos(2x) = 1 + cos(2x) 2. son inestimables. Derivadas de las funciones seno y coseno. Comenzamos nuestra exploración de la derivada de la función seno utilizando la fórmula para hacer una estimación razonable de su derivada. Recordemos que para una función f(x), f ( x), f′(x) = lím h→0f(x + h) − f(x) h. f ′ ( x) = lím h → 0 f ( x + h) − f ( x) h. En consecuencia, para.




