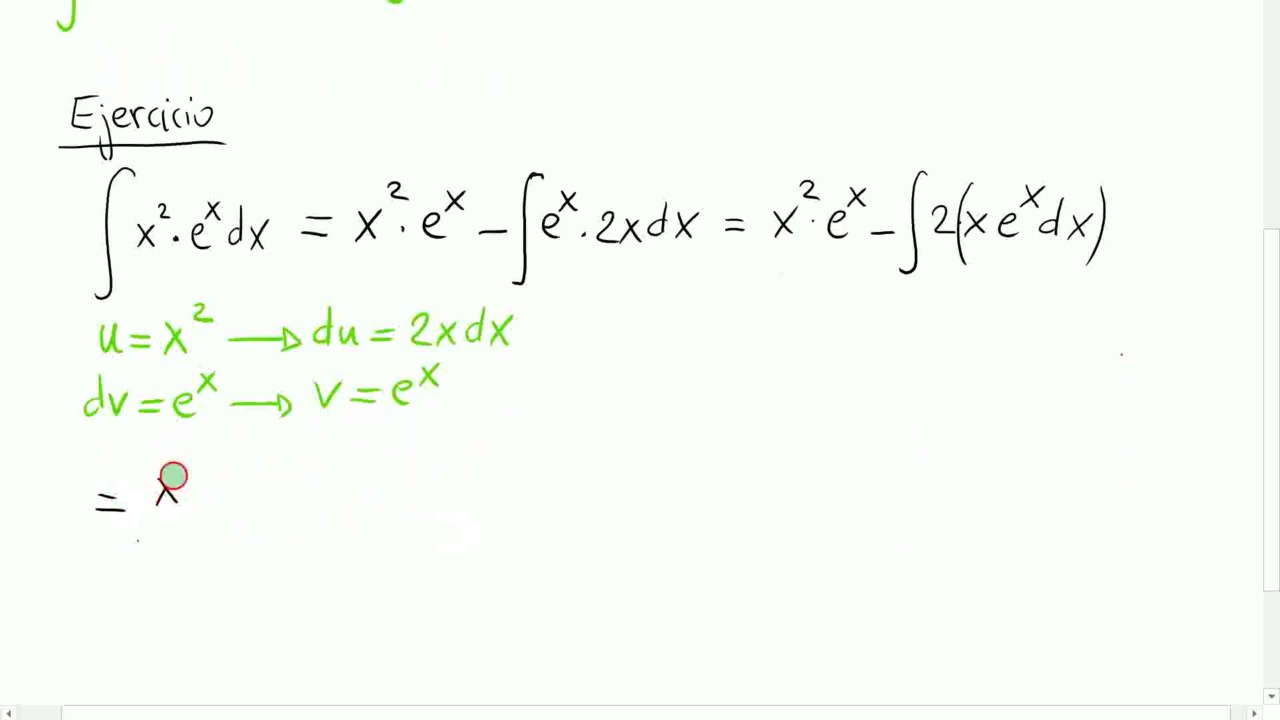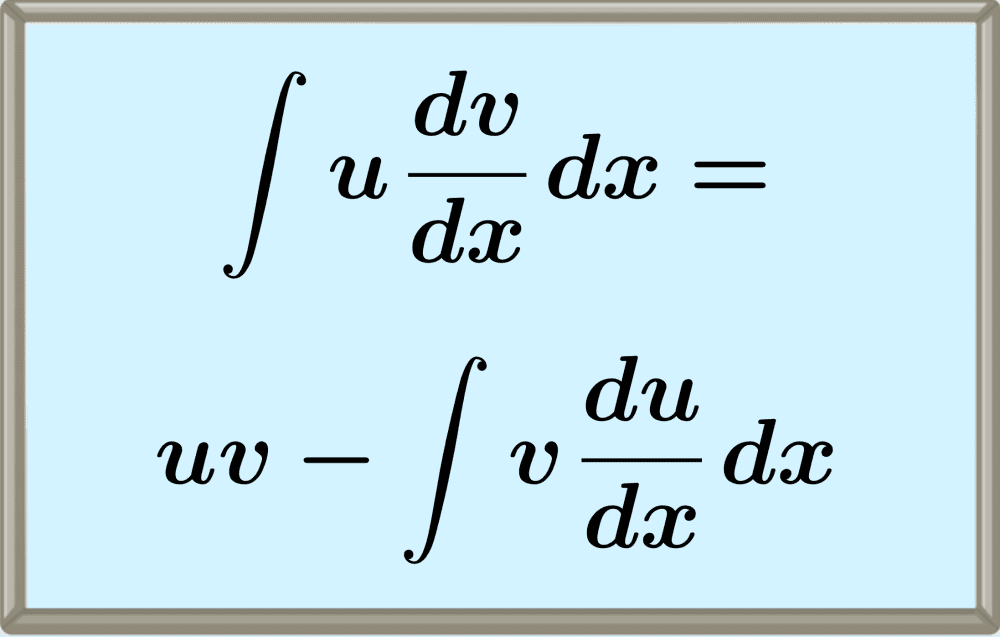Bienvenidos a nuestro blog dedicado a la fascinante y poderosa técnica matemática conocida como "integración por partes". Las integrales son una parte fundamental del cálculo, y en muchas ocasiones, pueden resultar desafiantes de abordar. Sin embargo, ¡no temas! La integración por partes es usada para integrar el producto de dos funciones. Para integrar funciones usando este método seguimos los siguientes pasos: 1. Escoge dos funciones, u y dv/dx El producto de las dos funciones, u\frac {dv} {dx} udxdv es el integrando. 2. Determina la derivada de u con respecto a x y la llamamos u ′ 3.
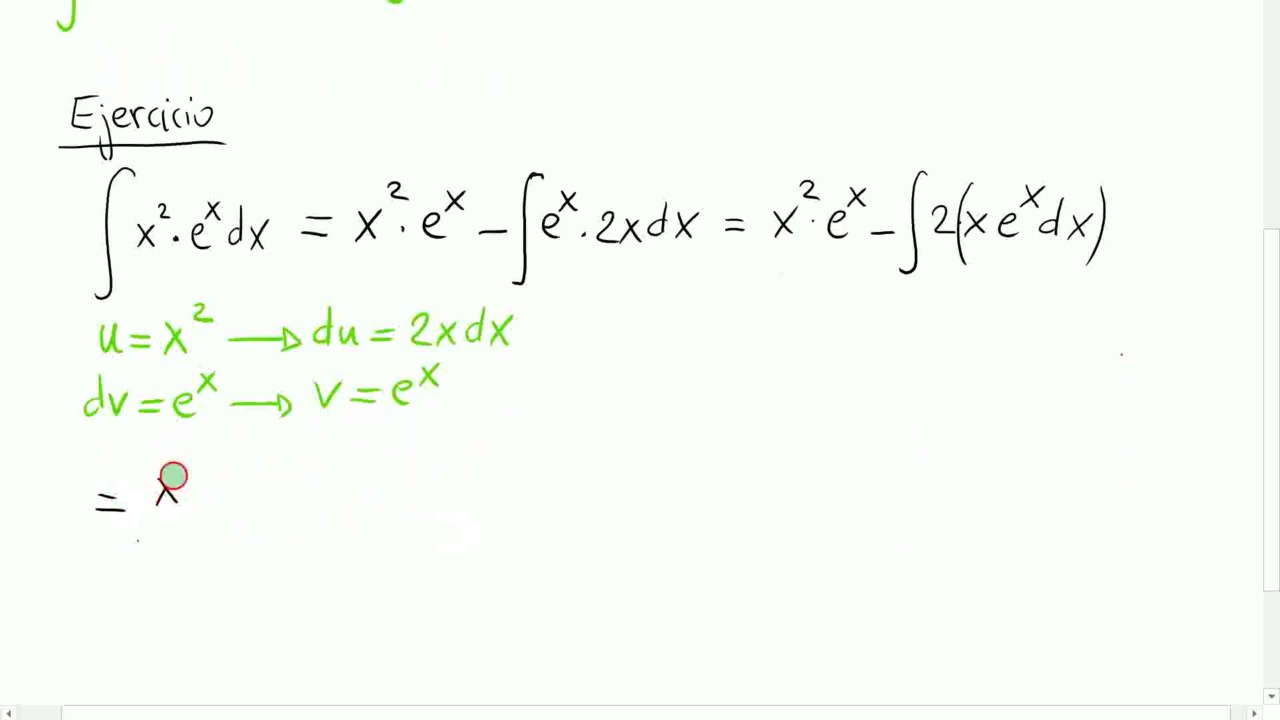
Integración por partes Ejercicio resuelto YouTube
Método: El integrando debe ser un producto de dos factores (si no lo es, podemos transformarlo para que lo sea). Uno de los factores será u u y el otro será dv d v . Se calcula du d u derivando u u y se calcula v v integrando dv d v . Se aplica la fórmula. Consejos Escoger adecuadamente u u y dv d v: Introducción a la integración por partes Integración por partes: ∫x⋅cos (x)dx Integración por partes: ∫ln (x)dx Integración por partes: ∫x²⋅𝑒ˣdx Integración por partes: ∫𝑒ˣ⋅cos (x)dx Integración por partes Integración por partes: integrales definidas Integración por partes: integrales definidas Desafío de integración por partes Entonces, la fórmula de integración por partes para la integral que involucra estas dos funciones es: ∫udv = uv − ∫vdu. (3.1) La ventaja de utilizar la fórmula de integración por partes es que podemos usarla para cambiar una integral por otra, posiblemente más fácil. El siguiente ejemplo ilustra su uso. julioprofe #julioprofe explica cómo resolver una integral por el Método de Integración por Partes.Tema: #Integrales → https://www.youtube.com/playlist?list=PLC6o1uTspYw.

Integrales por Partes Ejercicios Resueltos Fisimat
La integración por partes es un método para obtener integrales de productos: ∫ u ( x) v ′ ( x) d x = u ( x) v ( x) − ∫ u ′ ( x) v ( x) d x. o de manera más compacta: ∫ u d v = u v − ∫ v d u. Podemos usar este método, que se puede considerar como el inverso de la " regla del producto ," al considerar uno de los dos factores. Al utilizar la técnica de integración por partes, se debe elegir cuidadosamente qué expresión esu u. Para cada uno de los siguientes problemas, utilice las pautas de esta sección para elegiru u. No evaluar las integrales. 1) ∫x3e2x dx ∫ x 3 e 2 x d x Contestar 2) ∫x3 ln(x)dx ∫ x 3 ln ( x) d x 3) ∫y3 cos ydy ∫ y 3 cos y d y Contestar Integración por Partes para Integrales Definidas. Ahora que hemos utilizado con éxito la integración por partes para evaluar integrales indefinidas, dirigimos nuestra atención a integrales definidas. La técnica de integración es realmente la misma, solo que agregamos un paso para evaluar la integral en los límites superior e inferior de. 1.7: Integración por partes. El teorema fundamental del cálculo nos dice que es muy fácil integrar un derivado. En particular, sabemos que. \ begin {align*}\ int\ frac {d} {dx}\ izquierda (F (x)\ derecha)\, d {x} &= F (x) +C\ end {align*} Podemos explotar esto para desarrollar otra regla de integración, en particular una regla que nos ayude.
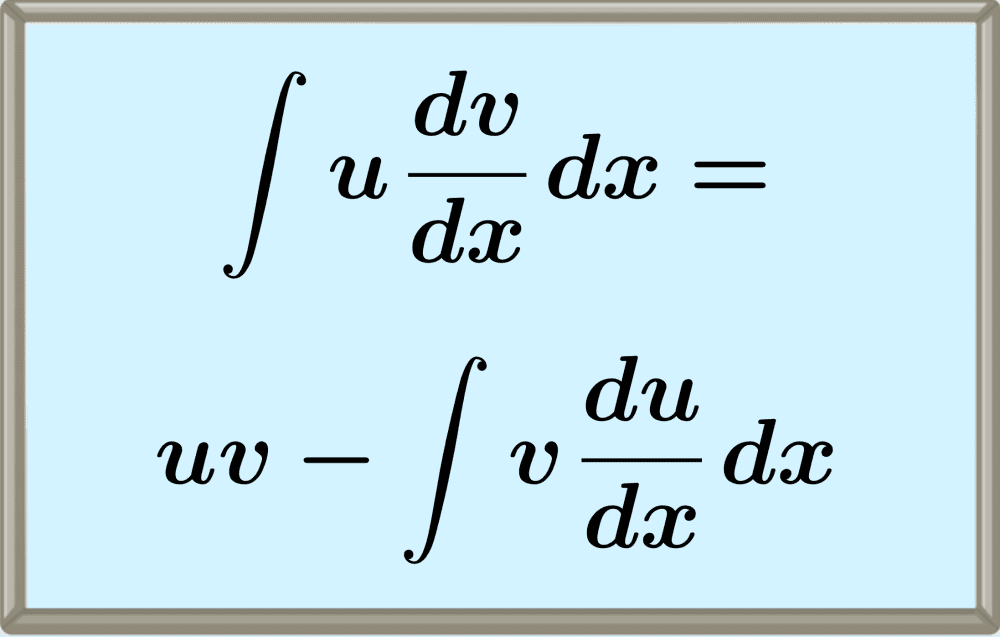
Integración por partes Ejercicios resueltos Neurochispas
Integración por partes Como veremos, la fórmula que se presentará será útil para integrar un producto de funciones, en las que, dependiendo de las características que éstas cumplan, es mejor seguir el siguiente patrón con el objetivo que la integral resultante en el miembro de la derecha sea más simple de calcular, que la integral original. El método de integración por partes se basa en la siguiente fórmula: Se utiliza cuando no es posible integrar por medio de las integrales inmediatas, ya que no es posible transformar la integral para que se parezca alguna de sus fórmulas. Date cuenta, que en la solución de la fórmula de integración por partes queda otra integral.
Para integrales que tienen la forma: En donde p (x) es un polinomio, se recomienda siempre hacer u = p (x), mientras que dv a la función trigonométrica o exponencial. Integración por partes En esta página explicamos el método de integración por partes paso a paso. Calcularemos 11 integrales mediante este método para ver el procedimiento. Este método se basa en la aplicación de la siguiente fórmula: ∫ u dv = u ⋅ v − ∫ v du ∫ u d v = u ⋅ v − ∫ v d u donde u u es una función y du d u es su derivada

EJERCICIOS RESUELTOS DE INTEGRALES POR PARTES PDF
Ejercicios resueltos de integración por partes I. Se trata de una integral racional que resolveremos dividiendo numerador entre denominador y aplicando la regla del cociente. Ver integrales racionales. Tipos que se pueden dar: producto de un polinomio por una función del tipo sen x , cos x ,a elevado x, e elevado x. #julioprofe explica cómo resolver una integral indefinida utilizando el Método de Integración por Partes. Tema: #Integrales → https://www.youtube.com/playlis.