Definición y propiedades de la parábola Es una curva cónica, abierta, plana y de una sola rama. Lugar geométrico de los puntos del plano que equidistan de uno fijo denominado foco y de una recta denominada directriz. Elementos Además del foco F y la directriz, cuenta con un eje de simetría E, normal a la directriz y que contiene al foco. 323 Share 19K views 2 years ago #Geometria #DibujoTecnico Tema completo de una de las tres curvas cónicas: la parábola. Definición, elementos, diferentes métodos de trazado, y una amplia colección.

14DIBUJO TÉCNICO LA PARÁBOLA DADO UN PUNTO Y EL FOCO (3) YouTube
SUSCRÍBETE: http://goo.gl/4lWWoY Explico paso a paso cómo dibujar una parábola en dibujo técnico, localizando puntos mediante los radios vectores y conociendo el foco y la directriz de la. La parábola es una curva plana, abierta y simétrica cuyos puntos equidistan de una recta (directriz) y de un punto (foco). Tiene un eje perpendicular a la directriz. La parábola es simétrica respecto a ese eje, en el que están situados tanto el foco como el vértice. El vértice, como punto de la curva que es, equidista del foco y la directriz. Parte 1 Dibujando una parábola Descargar el PDF 1 Aprende las partes de una parábola. Probablemente tengas determinada información antes de empezar y saber la terminología te ayudará a evitar cualquier proceso que no sea necesario. A continuación encontrarás las partes de la parábola que debes conocer: [1] El foco. Definición y elementos de la PARÁBOLA en Dibujo Técnico Eje, directriz, vértice, foco Curvas cónicas Dibujo Técnico, Miguel Fernández 1.64K subscribers Subscribe 1 Share 111 views 3 years ago.

Cómo dibujar una Parábola por Puntos mediante Radios Vectores conociendo el Foco y la Directriz
Curvas cónicas. La parábola es una curva abierta y plana, que se define como el lugar geométrico de los puntos del plano que equidistan de un punto denominado foco, y una recta denominada directriz, observando la figura, de la parábola es la recta perpendicular a la directriz, que pasa por el foco . La distancia FD, del foco a la directriz. 1. Definición de parábola 2. Elementos de la parábola 3. Construcción por puntos 4. Construcción de la parábola conocidos el eje, el vértice y un punto de la curva 5. Trazar una parábola conociendo el vértice y el foco. 6. Trazado mediante envolventes Definición de parábola La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y una recta llamada directriz. Los tres parámetros que definen una parábola son: Foco F: punto de tangencia de la esfera (tangente al cono) con el plano secante. Directriz d: recta intersección del plano X con el plano secante. Vídeos didácticos sobre curvas cónicas desde el enfoque del dibujo técnico. Trazados de elipses, determinación de tangentes y algunos aspectos teóricos. Trazado y Tangencias de Curvas Cónicas - Elipse, Parábola e Hipérbola - Elementos y Propiedades de las Curvas Cónicas.

Parábola, partes y propiedades, introducción teórica Dibujo Técnico Sin Ingedudas YouTube
Láminas - ejercicios de elipse, parábola, hipérbola - Dibujo Técnico Láminas - ejercicios de elipse, parábola, hipérbola Planteamientos y ejercicios resueltos de trazado de las curvas cónicas (elipse, parábola e hipérbola) y trazado de tangentes a cónicas. Valoración: Volver a Curvas cónicas. Hipérbola Volver a Curvas cónicas. Parábola Detalles Preguntas Tus notas Teoría y ejercicios resueltos Arturo Geometría Seguir canal Tema completo de una de las tres curvas cónicas: la parábola. Definición, elementos, diferentes métodos de trazado, y una amplia colección de ejercicios para que domines todos los casos posibles. 00:00 1.- Definición, circunferencia focal y tangente 02:41 2.-
- Dibujo técnico 1º de bachillerato - Dibujo técnico 2º de bachillerato - La parábola: trazados - 1. Trazado de la parábola dado el foco y la directriz Trazamos una paralela a la directriz a una distancia d. Con centro en F trazamos un arco de radio d que corta a la paralela en dos puntos pertenecientes a la parábola. Definición y esquema principal de la parábola, directriz, eje, recta recta tangente, circunferencias principal y focal. Esquema básico a seguir para resolver.
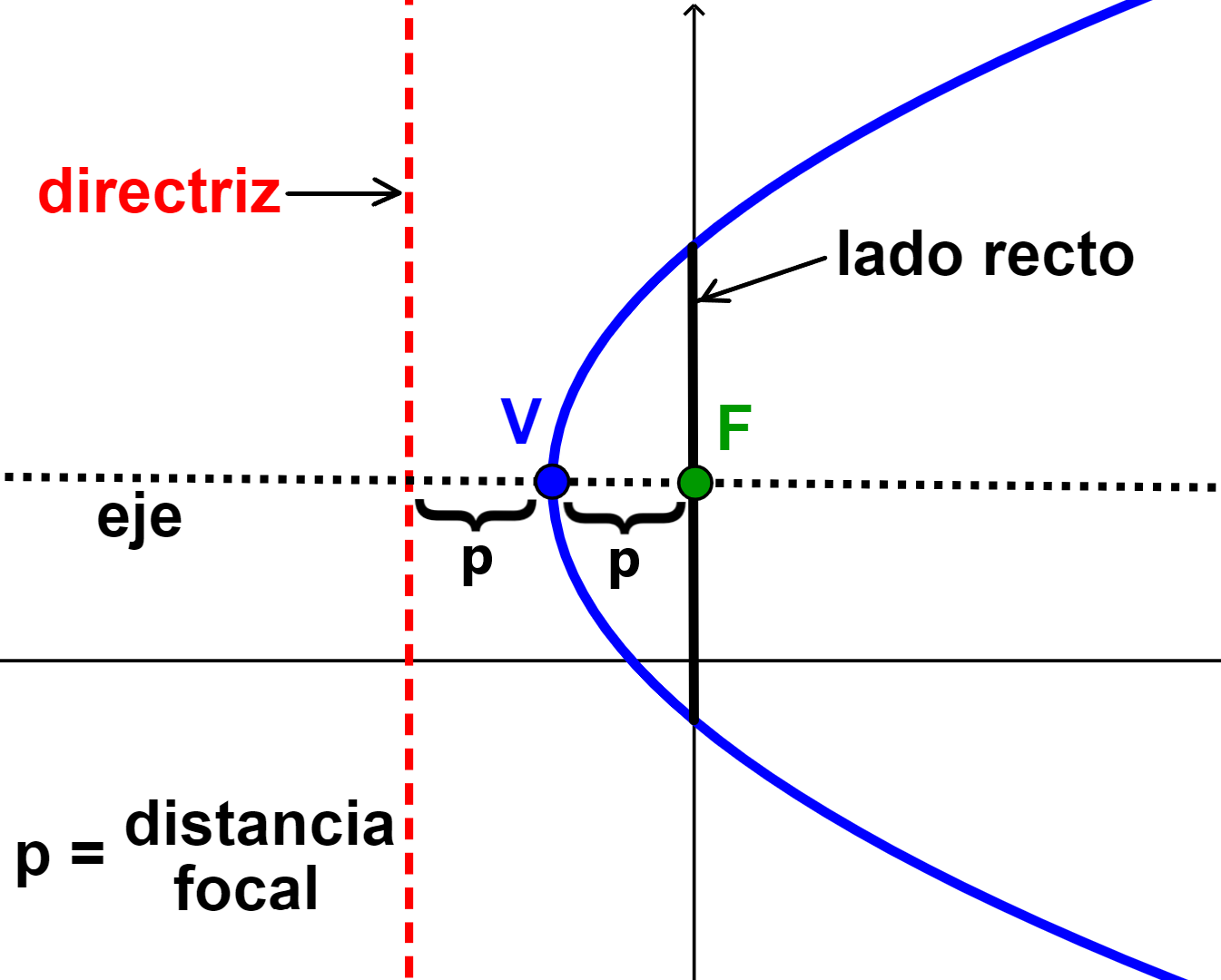
Elementos y Partes de una Parábola con Diagramas Neurochispas
Title /Users/Shared/Arquitectura/Dibujo Técnico/2013_Apuntes_002.dwg Author: Diego de Miguel Lería Created Date: 9/2/2012 5:56:33 PM Aquí tenéis en formato Mongge uno de los ejercicios de Parábolas en el que nos dan tan sólo un punto y el Foco de la curva. Y otro con el trazado de la tangente a la curva paralela a una dirección dada. - Ejercicio 2. Parábola conocidos dos puntos y el foco. - Ejercicio 3.




