Learn Practice Pentagonal Prism In geometry, a pentagonal prism is a three-dimensional shape with two pentagonal bases and five rectangular faces. So, a pentagonal prism has a total of 7 faces, 15 edges, and 10 vertices out of which 2 faces are pentagonal in shape. If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a truncated pentagonal hosohedron, represented by Schläfli symbol t {2,5}.
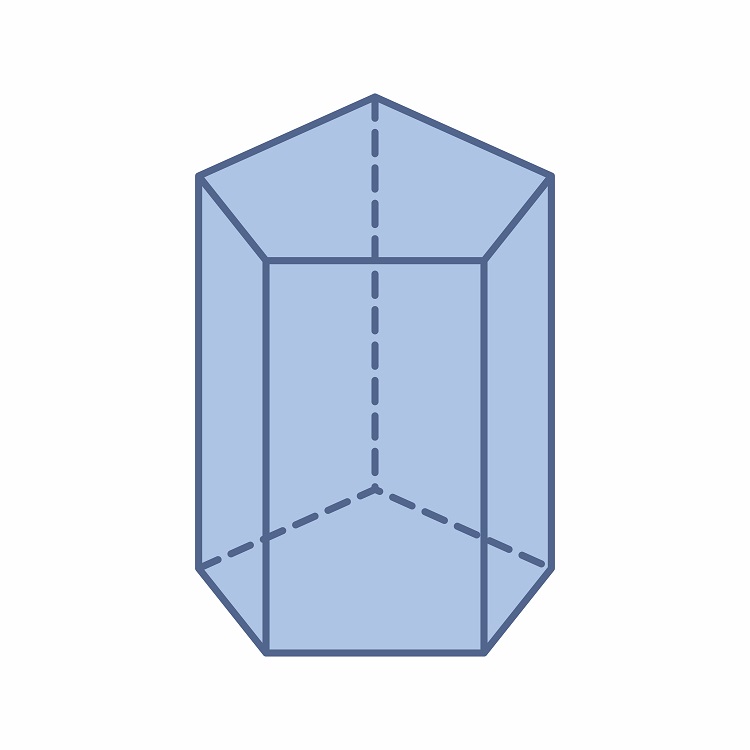
Prisma pentagonal características, partes, vértices, aristas, volumen
To calculate the volume of a regular pentagonal prism, we use the formula below: V = 5 / 2 × a × b × h. Plugging the values in the formula for the surface area of a regular pentagonal prism, we get. V = 5 / 2 × 10 × 20 × 15 = 7500 cubic cm. Thus, the volume of the chocolate box is 7500 cubic cm. The pentagonal prism is a prism having two pentagonal bases and five rectangular sides. It is a heptahedron. The regular right pentagonal prism is uniform polyhedron U_(76). Its dual polyhedron is the pentagonal dipyramid. A (possibly nonregular) pentagonal prism is the convex hull of the pentagrammic antiprism, pentagrammic prism, and pentagrammic crossed antiprism. Pentagonal Prism: Cross-Section: and more! Example: This hexagonal ice crystal.. Regular vs Irregular Prisms. All the previous examples are Regular Prisms, because the cross section is regular (in other words it is a shape with equal edge lengths, and equal angles.) Here is an example of an Irregular Prism: Irregular Pentagonal Prism: A prism is a right pentagonal prism when it has two congruent and parallel pentagonal faces and five rectangular faces that are perpendicular to the triangular ones. Volume and Surface Area of a Pentagonal Prime The two important measures made on a pentagonal prism are to find its volume and surface area. Volume of Pentagonal Prism Formula
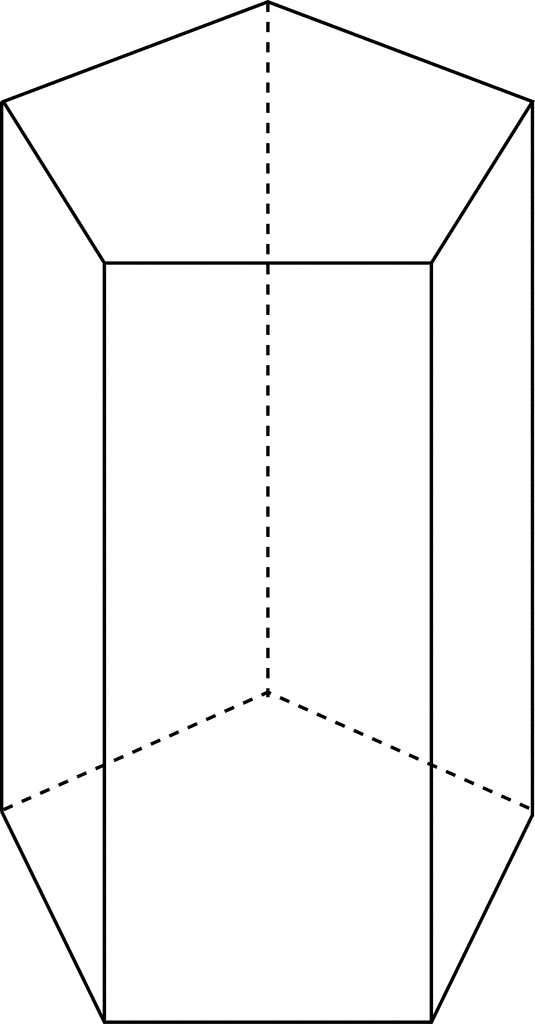
Pentagonal Prism ClipArt ETC
The volume of the pentagonal prism is defined as the capacity of the pentagonal prism. In geometry, a pentagonal prism is a three-dimensional shape with two pentagonal bases and five rectangular faces.So, a pentagonal prism has a total of 7 faces(out of which 2 faces are pentagonal in shape), 15 edges, and 10 vertices. By definition, there are 2 pentagonal bases that are congruent to each other. A right pentagonal prism can be regular when the base is a regular pentagon with equal base edges as shown in the above diagram or irregular when its base is an irregular pentagon with unequal base edges. Oblique Pentagonal prism. An oblique pentagonal prism is a slanted prism where the lateral faces are not perpendicular to the bases. Step 1: Find the base area of the given pentagonal prism. Base area = Area of pentagon. Base area = ( 1 2 × Perimeter) × Apothem. Base area = ( 1 2 × 5 b) × a Perimeter of a regular pentagon = 5 b. Step 2: Calculate the required volume using the formula: Volume of a pentagonal prism = 1 2 × a × 5 b × h cubic units. A pentagonal prism is a prism with the base of a pentagon. They can be regular, irregular, right or oblique but they each contain 7 faces, 15 edges, and 10 vertices.

Areas y volumen de un Prisma pentagonal Regular YouTube
Figure-5: Right pentagonal prism. Please note the characteristics of a pentagonal prism, such as its volume and surface area, can be calculated based on the lengths of its sides, the height of the prism, and the nature of its bases (whether they're regular or irregular).. Properties. A pentagonal prism, like any other prism, has a variety of geometric properties that define its shape and. Un prisma pentagonal es regular cuando los pentágonos que tiene como base son regulares. Esto quiere decir que sus lados y ángulos internos miden exactamente lo mismo. Se dice que este prisma es semi-irregular, puesto que no todas sus caras son igual entre sí. También te puede interesar:
Así pues, el área de un prisma pentagonal regular es igual a cinco por el lado del pentágono por la suma de la apotema más la altura. De modo que la fórmula del área de un prisma pentagonal regular es la siguiente: Puedes usar la calculadora que hay más abajo para calcular el área de cualquier prisma pentagonal regular. If the prism is a regular pentagonal prism, then the lateral faces are congruent. It has 7 faces, 15 edges, and 10 vertices. Two rectangular faces and a pentagonal face meet each other at each vertex. A pentagonal prism is right if the bases forms \( 90/degree \) with the lateral faces.

Pentagonal Prism Cuemath
Un prisma pentagonal es recto si las aristas laterales y las caras laterales son perpendiculares a las caras de la base, siendo las caras laterales rectangulares. En caso contrario, el prisma es oblicuo. Suele llamarse regular al prisma pentagonal recto, aunque realmente se trata de un poliedro semirregular . Área El prisma pentagonal es una estructura armoniosa que se usa en arquitectura y diseño de objetos, como por ejemplo el moderno edificio que se muestra en la figura superior. Los ventanales en forma de pentágono irregular forman la base de los prismas. [toc] Características del prisma pentagonal




