El doble de un número más la mitad de otro suman 7; y, si sumamos 7 al primero de ellos, obtenemos el quíntuplo del otro. Plantea un sistema de ecuaciones y resuélvelo para hallar dichos números. Problema nº 14.- Dos de los ángulos de un triángulo suman 122 . El tercero de sus ángulos excede en 4 grados al menor de los otros dos. Estudia la compatibilidad de los siguientes sistemas. Cuando exista, da su solución. a) − = − =− + = 2 1 1 5 x y x y xy b) + = − =− + = 2 1 1 5 x y x y y Solución: Son sistemas de 3 ecuaciones con 2 incógnitas. Para estudiar su compatibilidad basta con aplicar transformaciones de Gauss. El sistema será compatible cuando aparezca.
.gif)
RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES EJERCICIOS RESUELTOS MATEMÁTICAS 2 BACHILLERATO PDF
Sistema de ecuaciones lineales Existen diferentes métodos de resolución: Método de sustitución. Método de reducción. Método de igualación. En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Por ejemplo: + =7 5 −2 =−7} Método de Sustitución 630 CAPÍTULO 10 | Sistemas de ecuaciones y desigualdades W Sistemas de ecuaciones lineales y sus soluciones Un sistema de ecuaciones es un conjunto de ecuaciones con las mismas incógnitas. Un sistema de ecuaciones lineales es un sistema de ecuaciones en el que cada ecuación es li- neal. Una solución de un sistema es una asignación de valores para las incógnitas que hace 4.3: Resolver sistemas por eliminación. En los Ejercicios 1-8, utilice el método de eliminación para resolver cada uno de los siguientes sistemas. Consulta tu resultado manualmente, sin la ayuda de una calculadora. 1) x + 4y = 0 9x − 7y = − 43. Contestar. 2) x + 6y = − 53 5x − 9y = 47. Ejercicios resueltos de sistemas de ecuaciones lineales. En este artículo puedes encontrar más de 30 ejercicios resueltos sobre sistemas de ecuaciones lineales (de primer grado) y un montón de recursos, pistas y consejos que te van a ayudar a ser un experto (💪) en sistemas de ecuaciones. 👉 ¡Yo sólo quiero descargar los ejercicios!
.gif)
SISTEMAS DE ECUACIONES LINEALES EJERCICIOS RESUELTOS Y PARA RESOLVER PDF
Sustituimos en la primera ecuación (escribimos 7 en lugar de x) y resolvemos la ecuación: La solución del sistema es x = 7 e y = 18. Por tanto, los números buscados son 7 y 18. Podemos comprobar el resultado: Los dos números suman 25: 7 + 18 = 25. 7 + 18 = 25. El doble de uno de ellos (7) es igual a 14: 2 ⋅ 7 = 14. Los pasos a seguir son los siguientes en el siguiente ejemplo: ! +# =7 5! −2# =−7. En primer lugar, necesitamos preparar las dos ecuaciones, si es necesario, multiplicándolas por los números que convenga. En este caso, queremos reducir la "y" de nuestro sistema, por tanto, multiplicamos la primera ecuación por 2. Resolver un Sistema de Ecuaciones por Sustitución. En los siguientes ejercicios, resolver los sistemas de ecuaciones por sustitución. Ejercicio 5.2E. 1. {2x + y = − 4 3x − 2y = − 6. Responder. Ejercicio 5.2E. 2. {2x + y = − 2 3x − y = 7. Ejercicio 5.2E. 3. {x − 2y = − 5 2x − 3y = − 4. SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS . Ejercicio nº 1.- Pon un ejemplo, cuando sea posible, de un sistema de dos ecuaciones con tres incógnitas que sea:. Plantea un sistema de ecuaciones lineales para calcular cuántos helados de cada sabor se compran a la semana. b) Resuelve, mediante el método de Gauss, el sistema planteado.
.gif)
SISTEMAS DE ECUACIONES LINEALES CON DOS INCOGNITAS Y SUS MÉTODOS DE SOLUCIÓN EJEMPLOS Y
Ejercicios resueltos de sistemas de ecuaciones para secundaria obligatoria - ESO y bachillerato. Resolución por sustitución, igualación y reducción. Sistemas linelaes y no lineales. Ejercicios resueltos paso a paso y comentados. Tema 3 - Sistemas de ecuaciones - Matemáticas I - 1º Bachillerato 1 SISTEMAS DE ECUACIONES EJERCICIO 6 : Halla la solución de los siguientes sistemas, analítica y gráficamente: a) + = + = 4 2 2 3 3 2 x y x y b) = + − −= y x x y x 3 4 2 0 2 c) +−= = − 6 0 2 2 y x y x x d) += + = − 3 7 2
El método de Gauss-Jordan es una técnica para resolver sistemas de ecuaciones lineales mediante la eliminación de variables. En este documento se explica el procedimiento paso a paso, con ejemplos y ejercicios resueltos. También se incluye una breve introducción a la teoría de matrices y determinantes. Multiplicamos la primera ecuación por 105 y aislamos las x x: El mcm de 2, 10 y 7 es 70. Multiplicamos la segunda ecuación por 70: Sustituimos en esta ecuación la x x que acabamos de calcular: Calculamos x x sabiendo y = 0 y = 0: Por tanto, la solución del sistema es x =6/7 x = 6 / 7 e y = 0 y = 0: Ver Igualación.
.gif)
SISTEMAS DE ECUACIONES LINEALES , MÉTODO DE GAUSS EJERCICIOS RESUELTOS MATEMATICAS 1
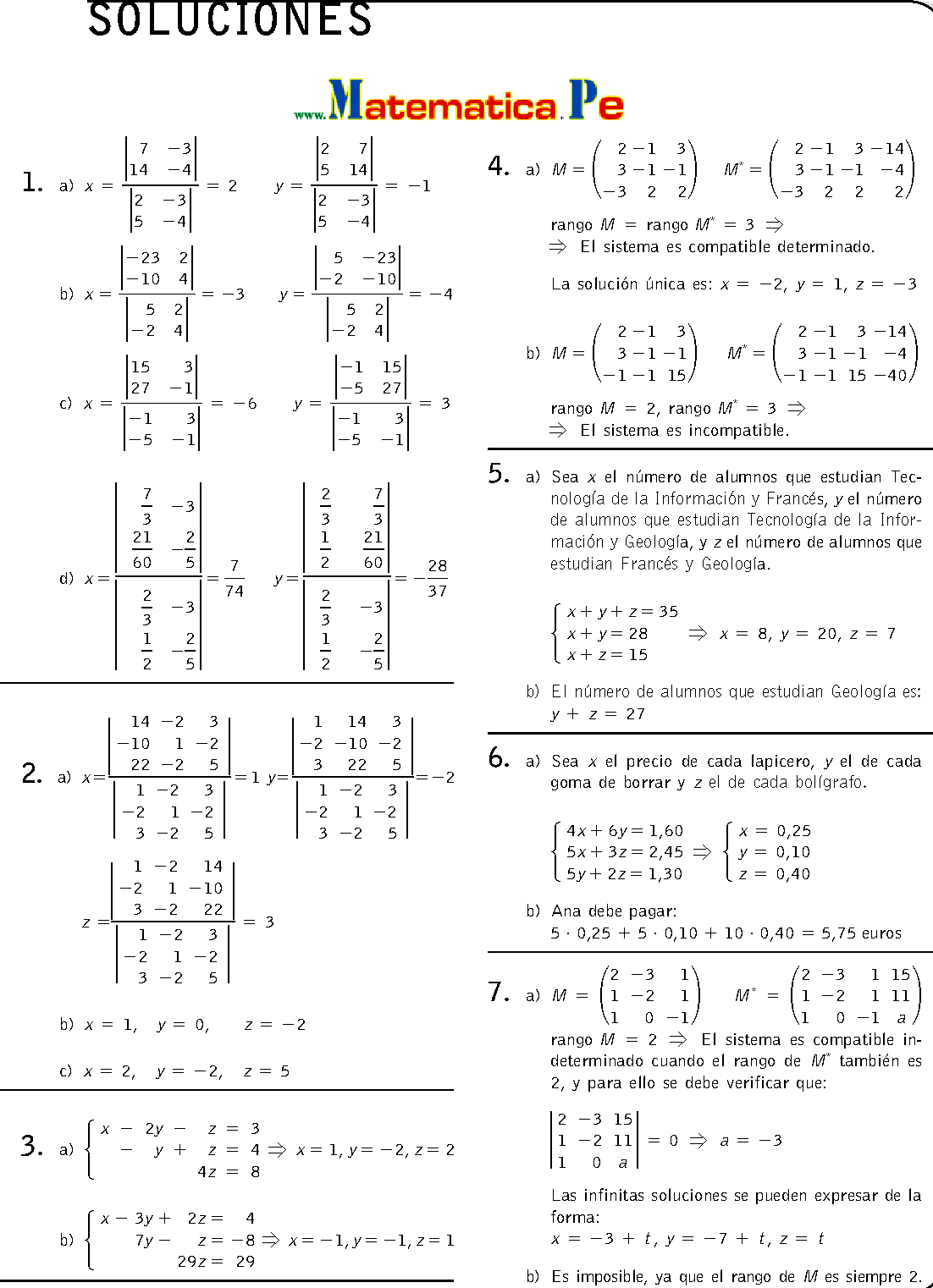
4 Sistemas de ecuaciones lineales 6.-Resolver, si es posible, el siguiente sistema de ecuaciones: x1 −x2 +x3 −x4 = 0 2x1 −2x2 +2x3 +x4 = 0 x2 +x3 +x4 = 0 Soluci on. El sistema anterior es un sistema homog eneo, por tanto es compatible. Adem as, el numero de inc ognitas es mayor que el numero de ecuaciones, as que es un sistema compatible. Luego debemos eliminar las de todas las ecuaciones, excepto la primera y la segunda ecuación. Este método es igual a la eliminación gaussiana, con la única diferencia de que no utilizamos la matriz asociada al sistema. 5 Resuelve el siguiente sistema utilizando el método de reducción: Solución. 6 Resuelve el siguiente sistema utilizando.
.gif)
.gif)
.gif)
.gif)
