Tabla de funciones trigonométricas son inscritos en una tabla y calculados valores de senos, cosenos, tangentes, cotangentes de los ángulos desde 0º hasta 360º. Usando la tabla de funciones tigonométricas Usted podrá hacer cálculos aunque no tenga a mano una calculadora para ingenieros. Tres razones trigonométricas comunes son : seno (sin), coseno (cos) y tangente (tan). Estas se definen para el ángulo agudo A como sigue: adyacente opuesto hipotenusa sin ( A) = opuesto hipotenusa cos ( A) = adyacente hipotenusa tan ( A) = opuesto adyacente A B C
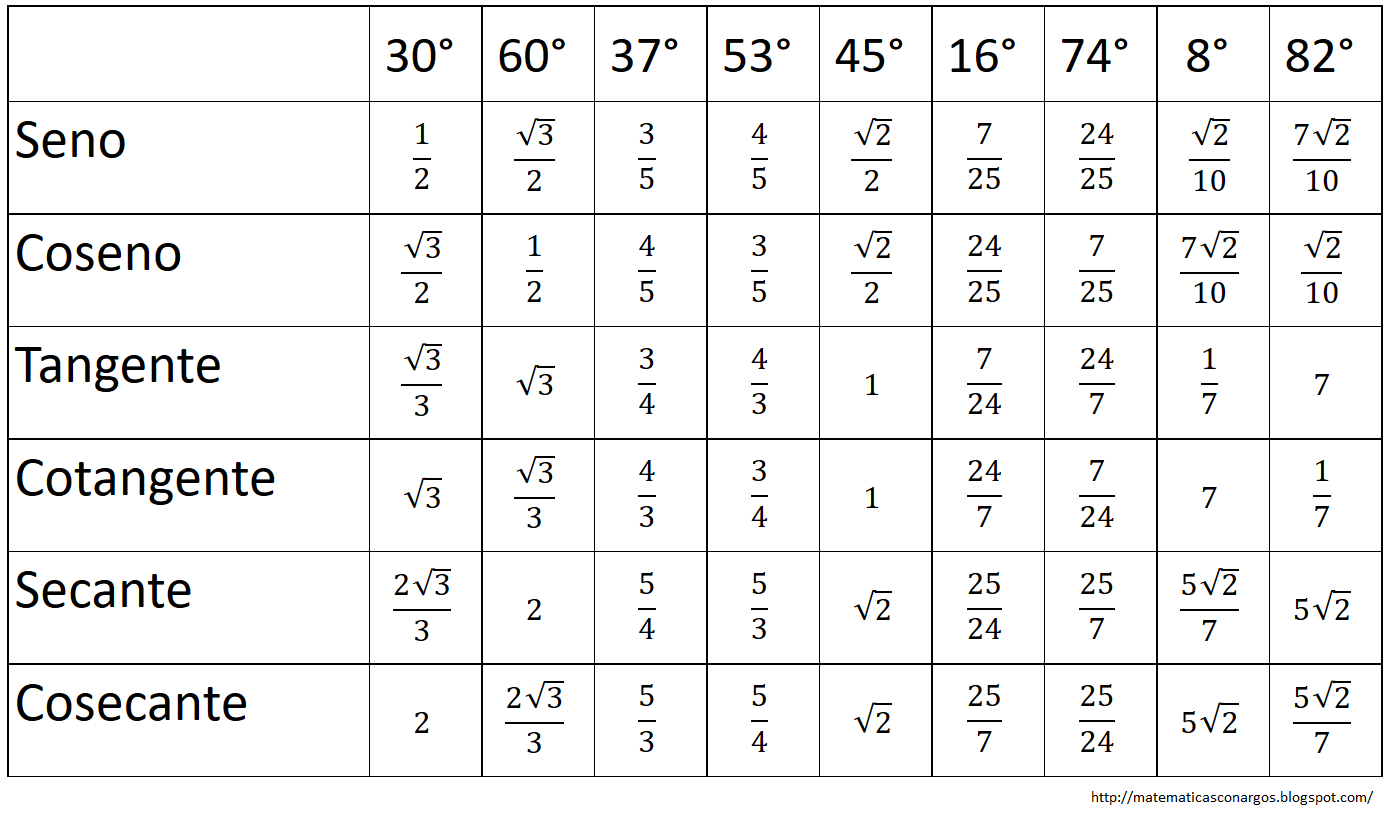
Matemática con Argos RAZONES TRIGONOMÉTRICAS
Tabla trigonométrica Como su nombre lo indica, es una tabla donde se exponen los valores de senos, cosenos y tangentes de los ángulos notables (desde 0° a 360°). Con ella podemos realizar cálculos en trigonometría sin necesidad de utilizar una calculadora. Razones trigonométricas de 0 °, 30°, 60° y 90°. Consideremos el siguiente triángulo: Repasa las seis razones tigonométricas: seno, coseno, tangente, cotangente, secante y cosecante. ¿Qué son las razones trigonométricas? C B A opuesto adyacente hipotenusa ¿Quieres apreder más acerca de seno, coseno y tangente? ¿Mira este video. ¿Quieres apreder más acerca de cotangente, secante y cosecante? Dale un vistazoa este artículo. Unidad 1: Triángulos rectángulos y trigonometría 0/700 puntos de dominio Razones en triángulos rectángulos Introducción a las razones trigonométricas Resolver un lado en un triángulo rectángulo mediante razones trigonométricas Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c. Sea α uno de los ángulos agudos del triángulo rectángulo. El seno de un ángulo α se define como la razón entre el cateto opuesto ( a) y la hipotenusa ( c ).
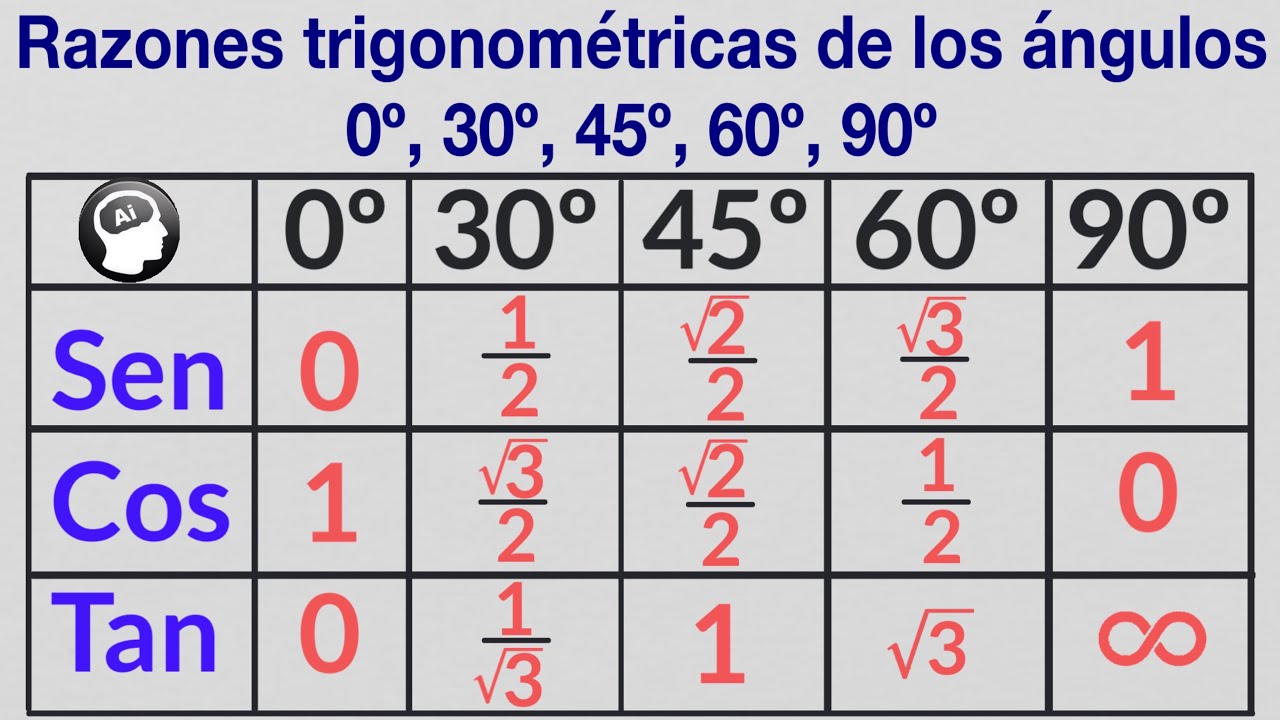
Razones trigonometricas de los angulos 0° 30° 45° 60° y 90° YouTube
Tablas Matemáticas de David: Tablas de Trigonometría PI = 3.141592. (aproximadamente a 22/7 = 3.1428) radianes = grados x PI / 180 (conversión desde grados a radianes) grados = radianes x 180 / PI (conversión desde radianes a grados) Los que tienen cero en el denominador son indefinidos. Son incluidos solamente para demostrar el modelo. Tabla 1.8 Ángulos comunes expresados en grados y radianes Ejemplo 1.22 Convertir radianes y grados Exprese 225° utilizando radianes. Exprese 5π/3 rad utilizando grados. Punto de control 1.17 Exprese 210° utilizando radianes. Exprese 11π/6 rad utilizando grados. Las seis funciones trigonométricas básicas Las razones trigonométricas recíprocas de los ángulos más característicos (0º, 30º, 45º, 60º, 90º, 180º y 270º) son:. En la siguiente tabla se puede ver la fórmula con la que se expresa cada una en función de la otra. Nota: el signo ± que corresponde en cada caso depende del cuadrante en que esté el ángulo. Tabla de razones trigonométricas . Relaciones pitagóricas entre las razones trigonométricas . Explicación: Como el triángulo que se considera dentro del círculo es rectángulo se cumple que En la imagen, los catetos (a y b) corresponden a los valores x y y, y la hipotenusa al radio, o sea , 1. Entonces

Tabla de Funciones Trigonométricas de 0 a 360 grados PDF
Examinemos más de cerca las principales razones trigonométricas: seno, coseno, tangente, cosecante, secante y cotangente. Seno (sen α) El seno de un ángulo α en un triángulo rectángulo es la razón entre el cateto opuesto a ese ángulo y la hipotenusa del triángulo. Matemáticamente, se expresa como: Tabla de las razones trigonométricas de los ángulos fundamentales 0 rad 6 π ra d 4 π ra d 3 π ra d 2 π ra d 3 2π ra d 4 3π ra d 6 5π ra d πra d 6 7π ra d 4.
Tabla de las razones trigonométricas de los ángulos notables. Regla nemotécnica para calcular los ángulos notables. Razones trigonométricas de los ángulos 30º, 45º y 60º deducidos a través de triángulos. Razones trigonométricas de los ángulos 0º, 90º, 180º y 270º deducidos a través de la circunferencia gonométrica. Las razones trigonométricas básicas del ángulo θ son sen θ, cos θ y tan θ, mientras que las restantes razones pueden expresarse en términos de estas tres. Del cuadro anterior se puede ver que: sec θ = 1/ cos θ cosec θ = 1/ sen θ cot θ = 1/tg θ

RAZONES TRIGONOMETRICAS DE ANGULOS NOTABLES DE 30° , 60° , 45° , 37° Y 53°/TEORIAEJEMPLOS
La tabla trigonométrica consiste en las razones trigonométricas, seno, coseno, tangente, cosecante, secante y cotangente. Los valores de las relaciones trigonométricas de los ángulos estándares son fundamentales para la solución de problemas de trigonometría. Descripción: Sitio web que al inicio presenta una tabla que contiene los valores de las funciones trigonométricas: seno, coseno, tangente, cotangente, de los ángulos desde 0º hasta 360º. Al final de esta tabla se pueden consultar otras. Teniendo a la mano estas tablas se podrán hacer cálculos sin necesidad de una calculadora para ingenieros.




