Solución: Para encontrar la transformada inversa, necesitamos cambiar la función de dominio s a una forma más simple: F ( s ) = 3 / ( s 2 + s - 6) = 3 / [ ( s -2) ( s +3)] = a / ( s -2) + b / ( s +3) [ a ( s +3) + b ( s -2)] / [ ( s -2) ( s +3)] = 3 / [ ( s -2) ( s +3)] a ( s +3) + b ( s -2) = 3 Tabla de Transformadas de Laplace CONTROL DE PROCESOS TRANSFORMACIÓN DE LAPLACE Definición [f(t)] = F(s) = e st f (t)dt 0 Propiedades 1. Linealidad [a f(t) + b g(t)] = a [f(t)] + b [g(t)] 2. Tranformación de funciones trasladadas [f(t-L)] = e-Ls [f(t)] 3. Tranformación de la diferenciación real [ df ( t)] = s F(s) - f(0) dt d 2 [

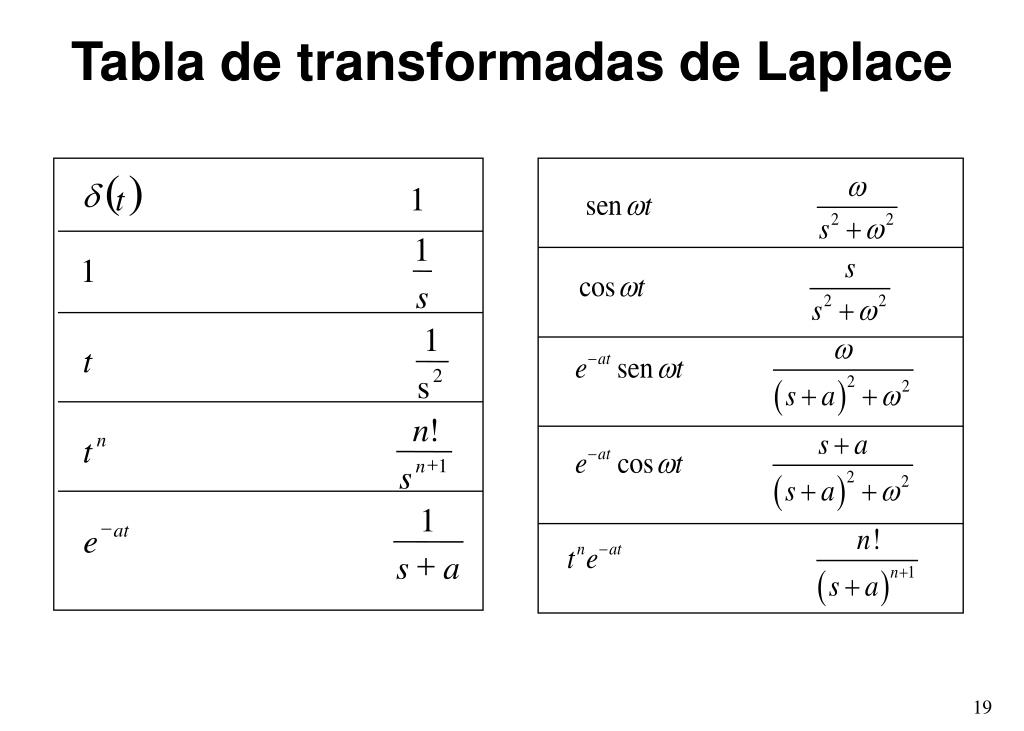
Tabla de Transformada de Laplace.
transformada de Laplace tabla de transformadas de Laplace transformada inversa de Laplace tabla de transformadas inversas de Laplace primer teorema de traslación segundo teorema de traslación teorema del valor inicial teorema del valor final Created Date: 8/23/2017 4:35:58 PM. Afortunadamente, podemos usar la tabla de transformaciones de Laplace para encontrar transformaciones inversas que necesitaremos. Ejemplo 8.2.1 Funciones exponenciales f (t) F (s)=L{f}(s) eat 1 s −a teat 1 (s−a)2 tneat n! (s−a)n+1, n entero y positivo ebt −eat t ln s−a s−b 1 √ πt e−a2/4t e −a √ s √ s a 2 √ πt3 e−a2/4t e−a √ s eat −ebt a−b 1 (s−a)(s−b) Una muestra de tales pares se da en la Tabla 5.2.1. Combinando algunas de estas simples transformaciones de Laplace con las propiedades de la transformación de Laplace, como se muestra en Table 5.2.2, podemos tratar muchas aplicaciones de la transformación de Laplace. Primero probaremos algunas de las transformaciones de Laplace dadas y.

Tabla de Transformada de Laplace
The direct Laplace transform or the Laplace integral of a function f (t) defined for 0 ≤ t < ∞ is the ordinary calculus integration problem ∞ 0 f (t)e −st dt, succinctly denoted L (f (t)) in science and engineering literature. The L-notation recognizes that integration always proceeds over t = 0 to t = ∞ and that the integral. Calculadora gratuita para transformadas de Laplace - Encontrar la transformada de Laplace y la transformada inversa de Laplace de funciones paso por paso Es fácil, mediante el uso de la Ecuación 14.1.2, derivar todas las transformadas que se muestran en la siguiente tabla, en la que t > 0. (¡Hazlo!) Esta tabla puede, por supuesto, ser utilizada para encontrar las transformadas inversas de Laplace así como las transformadas directas. vamos a continuar llenando nuestra tabla de transformadas de la plaza y una buena manera de hacerlo es escribir nuestra definición de la transformada de la plaza la transformada de la plaza de una función de t va a ser igual a la integral impropia de 0 infinito de al menos siete por efe dt dt esta es nuestra definición y la primera transformada de laplace que hicimos es la transformada de.

Tabla de transformadas de laplace
En matemáticas, la transformada de Laplace es una transformada integral que convierte una función de variable real (normalmente el tiempo) a una función de variable compleja . Tiene muchas aplicaciones en ciencia e ingeniería porque es una herramienta para resolver ecuaciones diferenciales. En el vídeo encontrarás varios ejercicios resueltos paso a paso para determinar las transformadas de Laplace utilizando tablas
Tabla de las transformadas de Laplace más comunes La siguiente tabla provee la mayoría de las transformaciones de Laplace para funciones de una sola variable. Debido a que la transformada de Laplace es un operador lineal, la transformada de Laplace de una suma es la suma de la transformada de Laplace de cada término. En esta ocasión te mostramos una introducción muy sencilla para encontrar las transformadas de Laplace, de la forma directa utilizando las tablas de las tran.
PPT La transformada de Laplace PowerPoint Presentation, free download ID1339192
Teorema de la transformada de la Integral. La ecuación 5.10 muestra cómo se aplica este teorema cuando se calcula la transformada de Laplace a una integral, esto es, se multiplica por 1 entre s la transformada de la función. El teorema de la transformada de la derivada como el de la integral son muy importantes ya que se utilizarán para. 5 Tabla de Transformadas de Laplace ¿Qué es la Transformada de Laplace? La Transformada de Laplace es un tipo de transformación integral creada por el matemático francés Pierre-Simon Laplace (1749-1827), y perfeccionada por el físico británico Oliver Heaviside (1850-1925), con el objetivo de facilitar la resolución de ecuaciones diferenciales.




