5) Halla x aplicando el teorema de Tales. Los dos triángulos son semejantes, por lo tanto, sus lados son proporcionales: 6) Sabiendo que AB = 15 cm, BC = 20 cm y A'B' = 12 cm, halla la longitud del segmento B'C'. ¿Qué teorema has aplicado? Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?.Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
El Teorema de Thales Ejercicios Resueltos Nivel 1 Paso a Paso YouTube
Dentro de la geometría y trigonométrica existe un teorema muy relevante por sus distintas aplicaciones, y se trata del teorema de Tales, en honor así al famoso matemático griego, este teorema recibe también el nombre de teorema básico de proporcionalidad. Este teorema se aplica en triángulos semejantes. EJERCICIOS TEOREMA DE TALES. (soluciones en la página 3) - Halla x e y en la siguiente figura: - Calcula x (todas las medidas están en centímetros). - Calcula x (las unidades son metros): - Calcula x e y (las unidades son metros): - Del siguiente dibujo conocemos: AC = 108 m, CE = 72 m, BF = 27 m. ¿Cuánto miden BC y CF? El Teorema de Tales se utiliza para predecir resultados geométricos en problemas de construcción y diseño. Esto se hace aplicando la proporcionalidad entre los lados de los triángulos para predecir los resultados deseados. El teorema también se puede aplicar para encontrar la medida de un lado desconocido de un triángulo dado. ¿Te gustó el video? Suscríbete aquí https://bit.ly/3KV34KfRecuerda dejarme tu like!Aprende a encontrar valores desconocidos en triángulos empleando el teorem.

Teorema de Thales (geometría) ejercicios resueltos YouTube
Si quieres practicar triángulos en posición de Tales, en esta página encontrarás ejercicios interactivos con soluciones y explicaciones. Aprende a aplicar el teorema de Tales para calcular longitudes desconocidas en figuras semejantes. En los siguientes ejercicios, exploraremos cómo aplicar el Teorema de Thales para resolver problemas prácticos y demostrar sus propiedades en situaciones del mundo real. A través de estos ejercicios, desarrollaremos una comprensión más profunda de este importante teorema y su relevancia en la resolución de problemas geométricos cotidianos. como usar el teorema de thales ( y triÁngulos semejantes ) para calcular medidas e incÓgnitas usando proporciones. Explicación del teorema de Tales. Cuando la ciudad de Mileto, situada en la costa griega, iba a ser atacada por los barcos enemigos, los soldados recurrieron a Tales. Necesitaban saber a que distancia se encontraba una nave para ajustar el tiro de sus catapultas. El genio matemático resolvió el problema sacando una vara por la cornisa del.

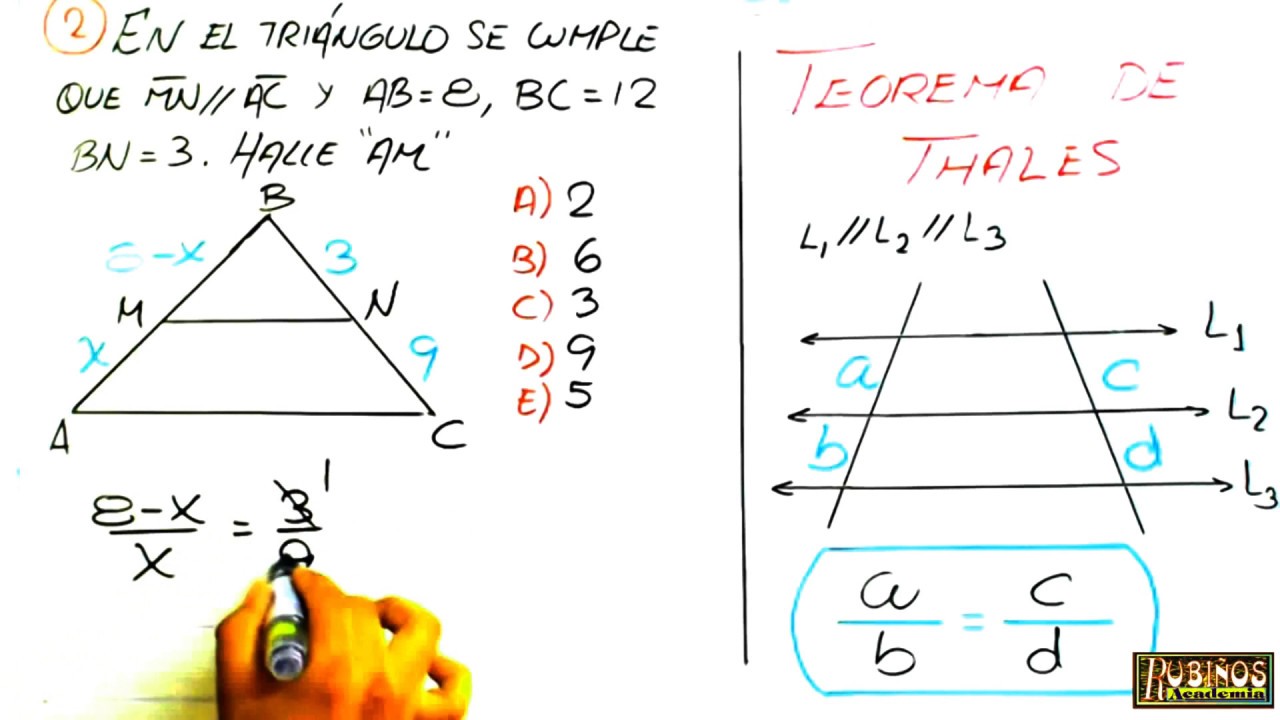
Ejercicios resueltos del Teorema de Thales
Resolución de ejercicios sobre el Teorema de Thales. Si quieres ves más videos de geometría ingresa a https://youtube.com/playlist?list=PLLbEdt_4_oi7qZfSISEN. Ejercicios y Problemas con el Teorema de Tales. El teorema de Tales nos dice que, un triángulo inscrito en un círculo, en donde, la hipotenusa corresponde al diámetro del círculo, siempre es un triángulo rectángulo. Este teorema puede ser demostrado usando la suma de ángulos interiores. A continuación, veremos un resumen del teorema de.
Página 2 de 5 2 Ejercicios 1. Aplicando el teorema de Tales, calcula el valor de x. (Sol: 3,2 cm) 2. Las baldas de la repisa representada en la figura son paralelas. Ventajas. 1) Los ejercicios del teorema de Thales resueltos permiten comprender de manera más clara y concreta la aplicación de este teorema en situaciones reales, lo que facilita su comprensión y asimilación. 2) Al tener los ejercicios resueltos, se pueden analizar paso a paso los procedimientos y cálculos utilizados para llegar a la.

TEOREMA DE TALES. Ejercicio resuelto YouTube
Teorema de Thales 1 Ejercicios del Teorema de Thales Se debe asumir que todas las rectas que parecen paralelas efectivamente lo son, aunque no siempre se indique tal situaci´on. La aplicación del Teorema de Thales es para demostrar que los segmentos son de igual tamaño. Los Teoremas son parte de la Geometría del plano, la cual se encarga de estudiar las figuras geométricas como el área, el perímetro y la relación entre ellas. Los Teoremas permiten establecer relaciones que siempre se van a cumplir dadas las.




