1/ Module d'un nombre complexe et norme. Soit base orthonormée du plan complexe. Et soit un vecteur du plan d'affixe . Par définition : Le nombre réel est appélé module de est égale à . Or si a pour coordonnées (x,y) d'après le théorème de pythagore D'où pour tout élément de ℂ , Il est également à remarquer et à savoir que : Pour cela c'est très simple : on trace un cercle trigo, et on prend un x PETIT !!! L'intérêt est le suivant : cos (x) est GRAND et sin (x) est PETIT. On s'en servira tout à l'heure. Si on veut exprimer cos (π - x), on place π - x, et on regarde où est son cosinus : Il ne reste plus que 2 étapes :

Cercle trigo
Cercle trigonométrique interractif avec affichage décochable du cos, sin, cot et tan. Cercle trigonométrique interractif avec affichage décochable du cos, sin, cot et tan. Accueil. Fil d'actualités. Ressources. Profil. Relations. Classroom. Téléchargements d'applications. Cercle trigonométrique interactif. On cherche alors un angle tel que cos(θ) = 2√ 2 et sin(θ) = 2√ 2. Le tableau ou le cercle nous permettent de trouver θ = π 4. Ensuite, on utilise la formule avec l'arctangente. θ = arctan(2 2) = arctan(1) = π 4. on trace le cercle trigonométrique, on place le point et on lit l'angle (cette méthode permet de trouver graphiquement. Définition. Tout nombre complexe z = 0 s'écrit sous la forme z = ∣z∣(cos(α) +isin(α)) appelée forme trigonométrique de z. Retrouvez la leçon et de nombreuses autres ressources sur la page 2. Formes trigonométriques et exponentielles. Apprendre à lire sur le cercle trigonométrique - Première Yvan Monka 2.35M subscribers Subscribe 37K Share 1.6M views 7 years ago Trigonométrie - 1èreS Dans cette vidéo, tu pourras apprendre à.
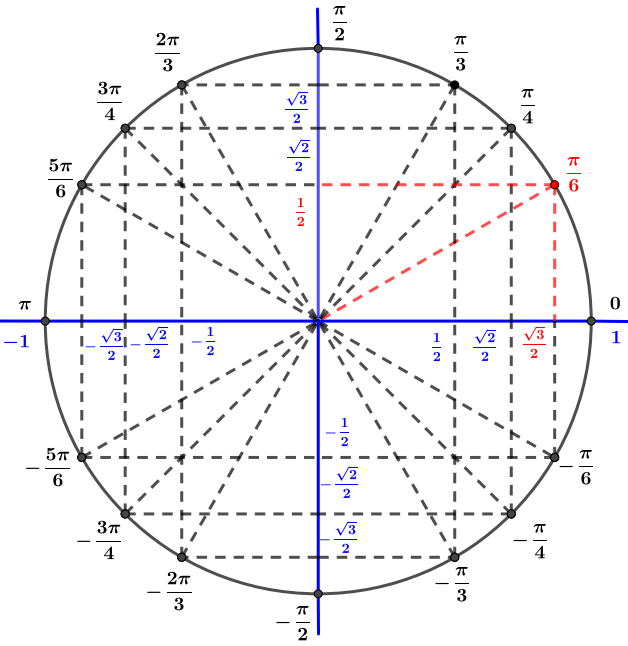
Déterminer la forme trigonométrique d'un nombre complexe Nombres complexes point de vue
La forme trigonométrique est la forme la plus adaptée à la multiplication et à la division de deux nombres complexes, en effet : z 1 = r 1 ( cos θ 1 + i sin θ 1) z 2 = r 2 ( cos θ 2 + i sin θ 2) ⇓ z 1 z 2 = r 1 r 2 [ cos ( θ 1 + θ 2) + i sin ( θ 1 + θ 2)] z 1 z 2 = r 1 r 2 [ cos ( θ 1 − θ 2) + i sin ( θ 1 − θ 2)] The unit circle definition allows us to extend the domain of sine and cosine to all real numbers. The process for determining the sine/cosine of any angle θ is as follows: Starting from ( 1, 0) . , move along the unit circle in the counterclockwise direction until the angle that is formed between your position, the origin, and the positive. Cercle, Nombres Complexes, Nombres. Cette appliquette montre l'affixe d'un point M du cercle trigonométrique dans le plan complexe. Nouvelles ressources. Construction q1; Inéquation du premier degré à 2 variables; Pente de la tangente; Empreintes de pieds dans le sable; Cercle trigonométrique BosseTesMaths 34.2K subscribers 361 Share 51K views 9 years ago 1ère spé maths Dans cette vidéo, tu vas comprendre le cercle trigonométrique, apprendre comment "enrouler".
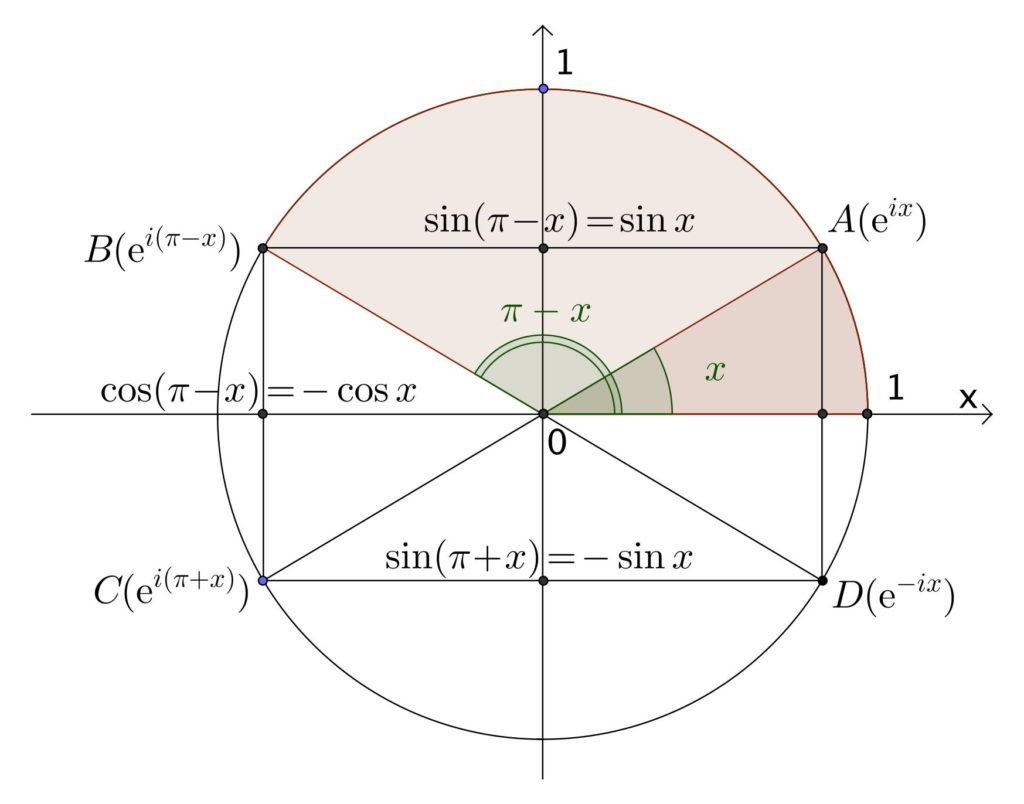
Trigonométrie circulaire Mathprepa
II) Forme trigonométrique d'un nombre complexe. Soit un nombre complexe non nul dont le module est r et un argument est On note : M le point image de. N l'intersection de la demi droite [OM) avec le cercle trigonométrique On a donc : Les coordonnées de N étant ( cos( ) ; sin( ) ) celles de M sont ( rcos( ) ; rsin( ) ) D'où on peut. 0:00 / 7:53 COMPRENDRE le cercle trigonométrique ! Hedacademy 752K subscribers 216K views 1 year ago 🎯 Tu veux la solution pour devenir solide en maths 💪 ? C'est ici :.
1) Cercle trigonométrique L'ensemble des points du plan complexe ("; %&⃗,)⃗) dont l'affixe appartient au cercle de centre O et de rayon 1 est noté x. Ce cercle s'appelle le cercle trigonométrique. Propriété : Soit -=++0, un nombre complexe appartenant à x. On a alors +++,+=1. 2) Stabilité de x . Nombres complexes de module 1 - Trigonométrie On note U l'ensemble des nombres complexes de module 1, qui se représente géométriquement par le cercle trigonométrique. Ainsi, pour tout nombre complexe z de module 1, il existe un réel θ tel que z = cosθ + isinθ . On note alors eiθ = cosθ + isinθ. En particulier, on a eiθ = eiθ θ ≡ θ ′ [2π] .

Le cercle trigonométrique comment le tracer et l'utiliser ? AuFutur
A partir de la fonction exponentielle complexe, on peut définir une fonction « exponentielle circulaire », qui « enroule » la droite réelle sur le cercle trigonométrique, et permet de définir rigoureusement les fonctions trigonométriques cosinus et sinus, qui s'étendent à tout le plan complexe, et de démontrer leurs propriétés élémentaires. %PDF-1.4 %âãÏÓ 141 0 obj > endobj xref 141 29 0000000016 00000 n 0000001641 00000 n 0000000876 00000 n 0000001725 00000 n 0000001915 00000 n 0000002077 00000 n 0000002608 00000 n 0000003088 00000 n 0000003536 00000 n 0000003669 00000 n 0000003909 00000 n 0000004165 00000 n 0000004411 00000 n 0000004782 00000 n 0000004859 00000 n 0000005928 00000 n 0000005964 00000 n 0000006920 00000 n.




